1. Законы классической механики. Задачи динамики.

1 закон: Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до те пора, пока приложенные силы не заставят ее изменить это состояние.

2 закон: Произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

3 закон: Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

4 закон: Если на материальную точку действуют несколько сил, то ускорение точки складывается из тех ускорений, которые имела бы точка под действием каждой силы.

Задачи динамики: Зная закон движения точки, определить действующие на неё силы. Зная действующие на точку силы, определить закон движения точки( реакцию наложенной силы)

2. Дифференциальные уравнения движения материальной точки в декартовых координатах и в проекциях на оси естественного трехгранника.

Так как действующие силы могут зависеть от времени t, от положения точки, т.е от ее координат, и от скорости, то в общем случае правая часть каждого из уравнений может быть функцией всех этих переменных одновременно. Разложим на оси касательной к траектории, вогнутость траектории и бинормаль.

3. Решение второй задачи динамики точки. Определение постоянных интегрирования.

x=x(t); y=y(t); z=z(t).

1. составить диф.уравнения движения.(нач.отсчета)

2. интегрирование диф.уравнения(по t, по х, по v)

3. Вычисление постоянных интегрирования

4. Дифференциальные уравнения относительного движения материальной точки. Переносная и кориолисова сила инерции.

…

Введём следующие обозначения:

=-переносная сила инерции,

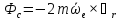=- сила инерции Кориолиса.

Это означает, что динамику относительного движения материальной точки в подвижной системе отсчёта, можно изучать на основе тех же уравнений Ньютона, добавляя к равнодействующей силе , переносную силу инерции и силу инерции Кориолиса

Относительное ускорение материальной точки тогда:

Переносное неравномерное:

………R- расстояние от точки до оси вращения. Переносная центробежная противоположна центростремительному ускорению.

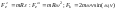. Переносное равномерное:

.

Поступательное Неравномерное:

_{Поступательное} равномерное прямолинейное перенос. И кориолиса =0. Нельзя механ.эксперементом определить в покое или нет. Принцип относительности классич.механ.

_{Мат.точка покоится относительно подвиж.системы а=0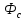,=0=>=0 =>}

5. Принцип относительности

классической механики. Случай

относительного покоя

точки.

Никакие механическим эксперементом нельзя обнаружить, находится ли данная мех.система отсчета в покое или совершает поступат.прямилин.движен. .()

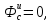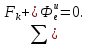В случае когда материальная точка находится в состоянии относительного покоя , следовательно игеометрическая сумма приложенных к точке сил и переносной силы инерции равна нулю.уравнен.относит.равновесия составляются так же, как уравнения равновесия в неподвиж.осях, если при этом к действующ.на точку силам взаимодействия с др.телами добавить переносную силу инерции.