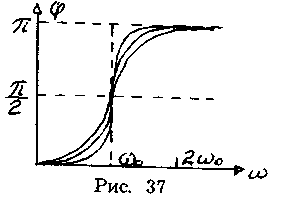5.7. Вынужденне колебания. Дифференциальное уравнение вынужденных колебаний и его решение.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью к.-л. периодически действующего фактора x(t), изменяющегося по гармоническому закону:

.

Если рассматривать механические колебания, то роль x(t) играет внешняя вынуждающая сила

., изменяющаяся с частотой (5.36)

С учетом силы (5.36) закон движения для пружинного маятника за­пишется в виде

.(5.37)

Используя (5. 15) и (5.30), придем к уравнению

. (5.38)

Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными меха­ническими.

Уравнение (5.38) можно свести к линейному неоднородному дифференциальному уравнению

,(5.39)

применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (х₀ в случае механических колеба­ний равно F₀/m).

Решение уравнения (5.39 равно сумме общего решения

(5.40)

однородного уравнения и частного решения

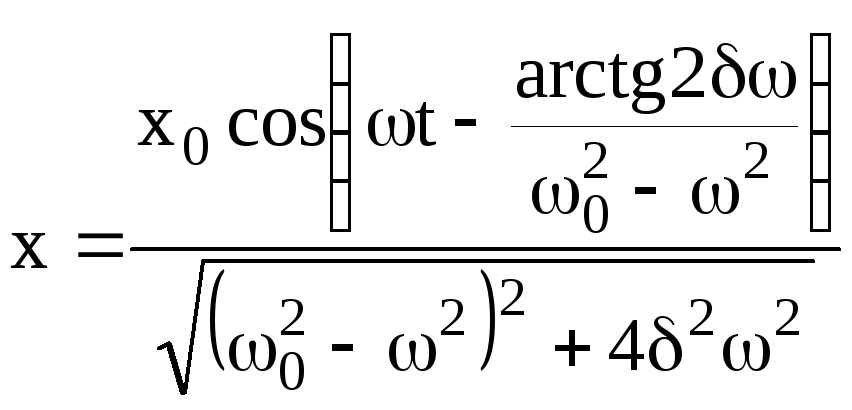(5.41)

неоднородного уравнения (5.39), где

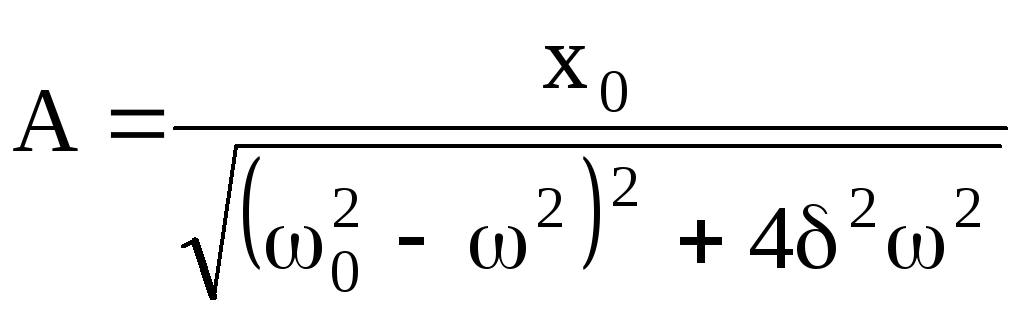, (5.42)

. (5.43)

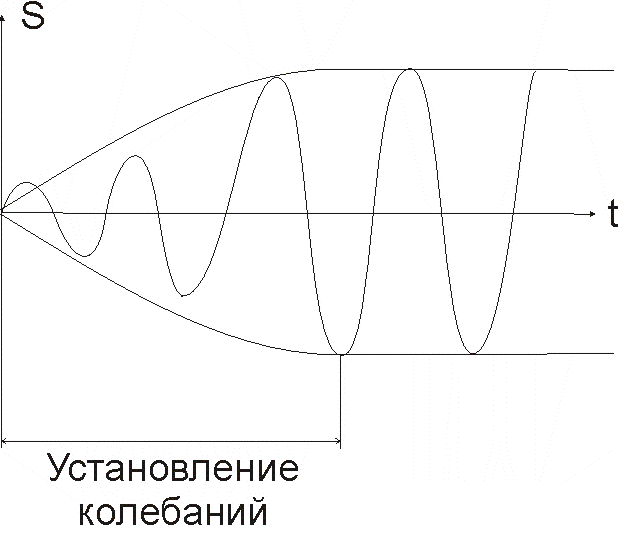
Слагаемое (5.40) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого ра­венством (5.42).

Рис. 35

Следовательно, в установившемся режиме вынужден­ные колебания происходят с частотой  и являются гармоническими; амплитуда и фаза колебаний также зависят от . Графически вынужденные колебания представлены на рис. 35.

5.8. Амплитуда и фаза вынужденных колебаний. Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты .

Чтобы определить резонансную частоту - час­тоту, при которой амплитуда А смещения достигает максимума, - нуж­но найти максимум функции или, что то же самое, минимум подкорен­ного выражения. Продифференцировав подкоренное выражение по w и приравняв к нулю, получим условие, определяющее :

.

Это равенство выполняется при , у которого только лишь положительное значение имеет физический смысл. Следователь­но, резонансная частота

.(5.44)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте называ­ется резонансом. При значение практичес­ки совпадает с собственной частотой ₀ колебательной системы.

Подставляя (5.44) в формулу (5.42), получим

. (5.45)

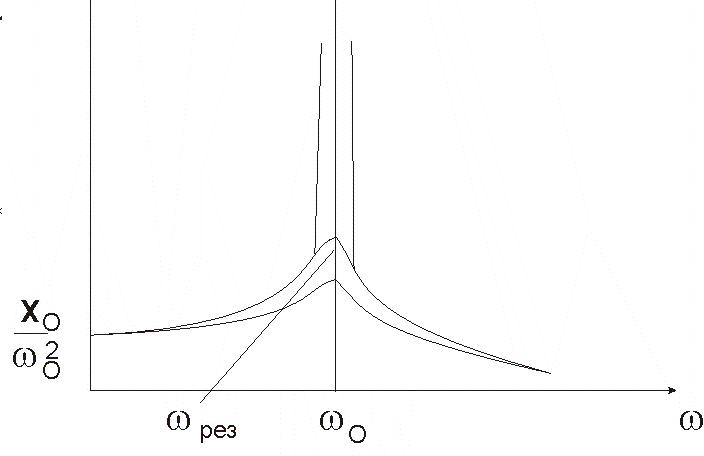
На рис. 36 приведена зависимость ампли­туды колебаний от частоты при различ­ных δ.

Из (5.44) и (5.45) вытекает что, чем меньше δ, тем выше и правее ле­жит максимум данной кривой. Если 0, то все кривые приходят к одному и тому же, отличному от нуля, предельному значению так называемому статическому отклонению.

Рис. 36

В случае механических колебаний . Если , то все кри­вые асимптотически стремятся к нулю. Приведенные на рис. 36 кри­вые называются резонансными кривыми.

Из формулы (5.46) вытекает, что при малом затухании резонансная амплитуда смещения

, (5.46)

где Q - добротность колебательной системы (5.35), - статическое отклонение. Отсюда следует, что добротностьQ характе­ризует резонансные свойства колебательной системы: чем больше Q, тем больше .

Зависимость от при разных коэффициентах  графически представлена на рис.37, из которого сле­дует, что при изменении  изменяется и сдвиг фаз .

Из формулы вытекает, что при =0 =0, а при =0 независимо от значения коэффициента затухания , т.е. вынуждающая сила опережает вынуждающие по фазе колебания на.

При дальнейшем увеличении  сдвиг фаз возрастает и при ₀, т.е. фаза колебаний почти противоположна фазе внеш­ней силы. Семейство кривых, изображенных на рис. 37, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы их собственная частота колебаний не совпадала с частотой возможных внешних воздействий, в противном случае воз­никнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить очень слабые колебания, если их частота совпадает с частотой собственных колеба­ний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.