
- •Механика и молекулярная физика
- •Физика измерения
- •1. Классификация ошибок измерения
- •2. Вероятность события
- •3. Распределение случайных ошибок измерения. Доверительный интервал и доверительная вероятность
- •5. Обработка результатов косвенных измерений
- •Лабораторная работа 1
- •Лабораторная работа 2
- •Лабораторная работа 3
- •Теоретические сведения
- •Из равенства (4) получаем
- •Воспользуемся формулой для радиуса кривизны нейтральной линии
- •Описание установки для измерения стрелы прогиба
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа 4
- •Лабораторная работа 5
- •Описание установки
- •Лабораторная работа 6
- •Лабораторная работа 7
- •Лабораторная работа 8
- •Лабораторная работа 9
- •Лабораторная работа 10
- •Лабораторная работа 11
- •Библиографический список
- •Оглавление
Из равенства (4) получаем
![]() .
(7)
.
(7)
Используя выражения (5) и (6), из (7) находим, что
![]() .
(8)
.
(8)
Выражение (8) является законом Гука в современной формулировке. Из него следует, что продольная деформация прямопропорциональна соответствующему нормальному напряжению
![]() .
(9)
.
(9)
Томас Юнг указал, что закон Гука справедлив только в пределах упругих деформаций материала. На рис. 1б представлена зависимость относительной линейной деформации бруска от нормального напряжения. Из (8) можно найти значение модуля продольной упругости материала
![]() (10)
(10)
или
![]() .
(11)
.
(11)
Таким образом, модуль упругости равен тангенсу угла наклона прямой к оси абсцисс (рис. 1б).
В данной работе модуль Юнга определяется по величине прогиба балки. Для этого необходимо найти зависимость стрелы прогиба балки от модуля Юнга, геометрических параметров балки и нагрузки.
Рассмотрим изгиб балки прямоугольного сечения под действием силы, приложенной к центру балки (рис. 2). Внутренние силы, обусловленные взаимодействием частиц (атомов и молекул), сохраняют форму и целостность тела. Внешние силы стремятся изменить взаимное расположение частиц, т.е. деформировать это тело. При этом возникают дополнительные внутренние силы, препятствующие этой деформации.
Обозначим
стороны прямоугольника, лежащего в
сечении, через а
и в,
а длину балки -
![]() (рис. 2).
(рис. 2).
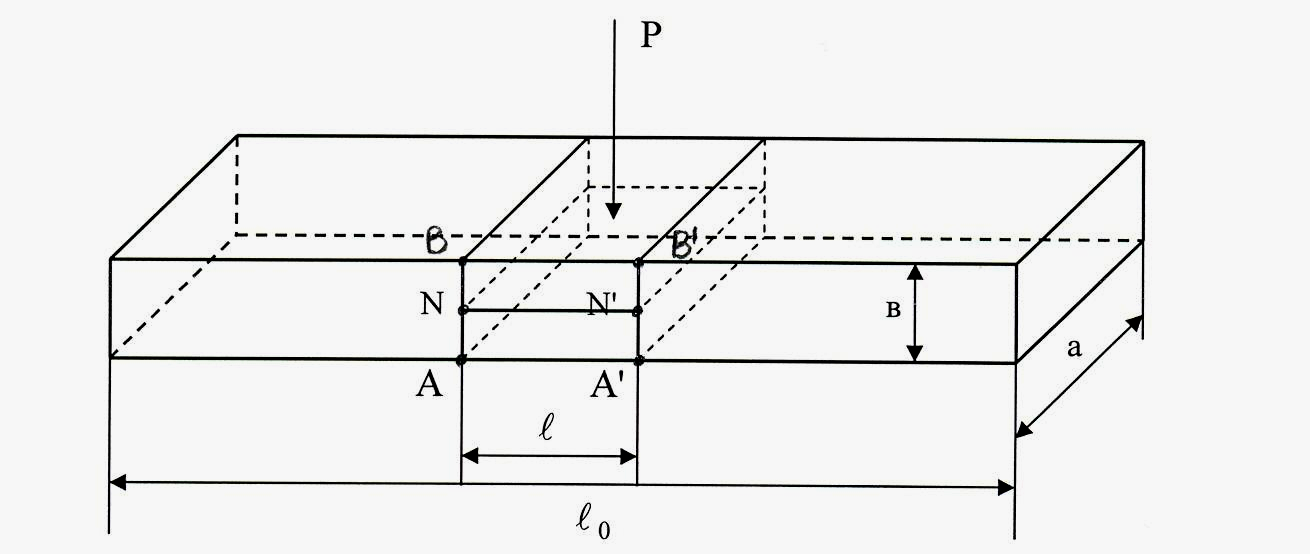
Рис.2
Обозначим
стороны прямоугольника, лежащего в
сечении, через а
и в,
а длину балки -
![]() (рис. 2). Пусть до деформации элемент
балки имел форму прямоугольного
параллелепипеда. Мысленно проведем два
близких нормальных сечения, т.е. вырежем
малый элементААВВ,
длину которого обозначим
(рис. 2). Пусть до деформации элемент
балки имел форму прямоугольного
параллелепипеда. Мысленно проведем два
близких нормальных сечения, т.е. вырежем
малый элементААВВ,
длину которого обозначим
![]() .
В результате изгиба элементаААВВ
все прямые, параллельные АА
и ВВ,
перейдут в дуги окружностей с центрами,
лежащими на оси, проходящей через точку
О перпендикулярно
плоскости рисунка (рис. 3).
.
В результате изгиба элементаААВВ
все прямые, параллельные АА
и ВВ,
перейдут в дуги окружностей с центрами,
лежащими на оси, проходящей через точку
О перпендикулярно
плоскости рисунка (рис. 3).
При
малых деформациях слои, лежащие выше
линии NN,
сжимаются, а слои, лежащие ниже линии
NN,
удлиняются. При этом длина нейтральной
линии NN
остается неизменной. Пусть R
– радиус
кривизны нейтральной линии. Тогда
![]() ,
где
- угол, выраженный в радианах.
,
где
- угол, выраженный в радианах.
Рассмотрим
слой балки, находящийся ниже линии NN
и имеющий толщину
(R).
Длина рассматриваемого слоя
![]() ,
а изменение длины
,
а изменение длины![]() .
.
Используя выражение (7), можно записать
![]() ,
(12)
,
(12)
где F – внутренняя сила, действующая на площадь A нормального сечения рассматриваемого слоя.
Напряжение, обусловленное внутренней силы, равно:
=![]() .
(13)
.
(13)

Рис.3.
Предположим, что при изгибе все нормальные сечения остаются плоскими (гипотеза Бернулли). Сумма напряжений, созданных внутренними силами и действующих на плоскость нормального сечения, равна нулю:
N
=![]() ,
(14)
,
(14)
где интеграл берется по площади нормального сечения A. Это является результатом того, что слои, лежащие выше нейтральной линии, сжимаются, а слои, лежащие ниже этой линии, удлиняются. Таким образом, напряжения выше и ниже нейтральной линии имеют разные знаки.

Рис. 4
Рассечем балку плоскостью AB, перпендикулярной нейтральной линии NN'. Установим систему координат X1Y1Z1 так, чтобы ее начало совпадало с центром тяжести C нормального сечения (рис. 4). Ось X1 проходит через нейтральную линию NN, а ось Y1 направлена вниз. Рассмотрим внутренние силовые факторы, действующие на эту отсеченную часть балки со стороны отброшенной ее части.
Изгибающий момент Mx1 , созданный внутренними силами относительно оси X1, равен
![]() ,
(15)
,
(15)
где
![]() - момент инерции сечения относительно
осиX1:
- момент инерции сечения относительно
осиX1:
![]() .
(16)
.
(16)
Выберем систему координат XYZ такую, чтобы ось ОZ была направлена вдоль нейтральной линии NN, а ось OY – перпендикулярно оси ОZ (рис. 5). Поместим начало координат в точку O, расположенную над левой опорой. Тогда уравнение для нейтральной линии изогнутой балки представится в виде у=у(z). Причем верхняя и нижняя линии балки смещены, соответственно, вверх и вниз на b/2 от нейтральной линии.
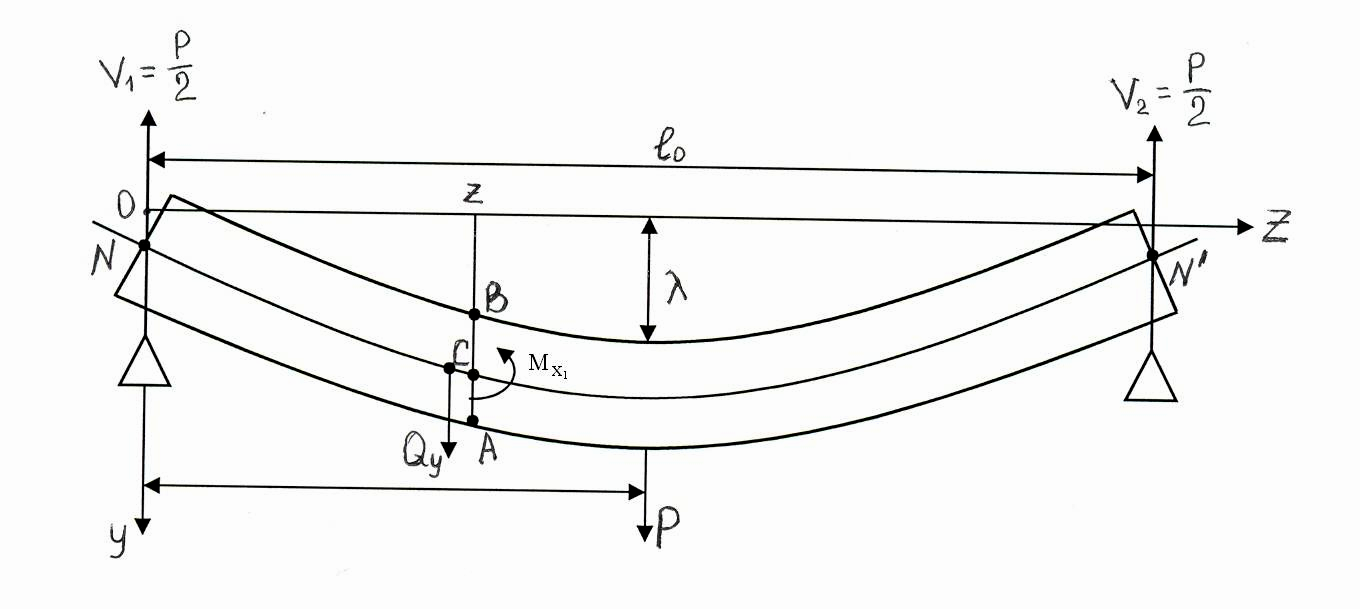
Рис. 5
