§ 3 Основные теоремы теории вероятностей:
3.1. Теоремы сложения. 3.2.Теоремы умножения. 3.2.1.Условная вероятность.
3.3. Формула полной вероятности. Формула Байеса.
Несколько событий называются совместными (несовместными), если появление одного из них в единичном испытании не исключает (исключает) появления других событий в этом же испытании.
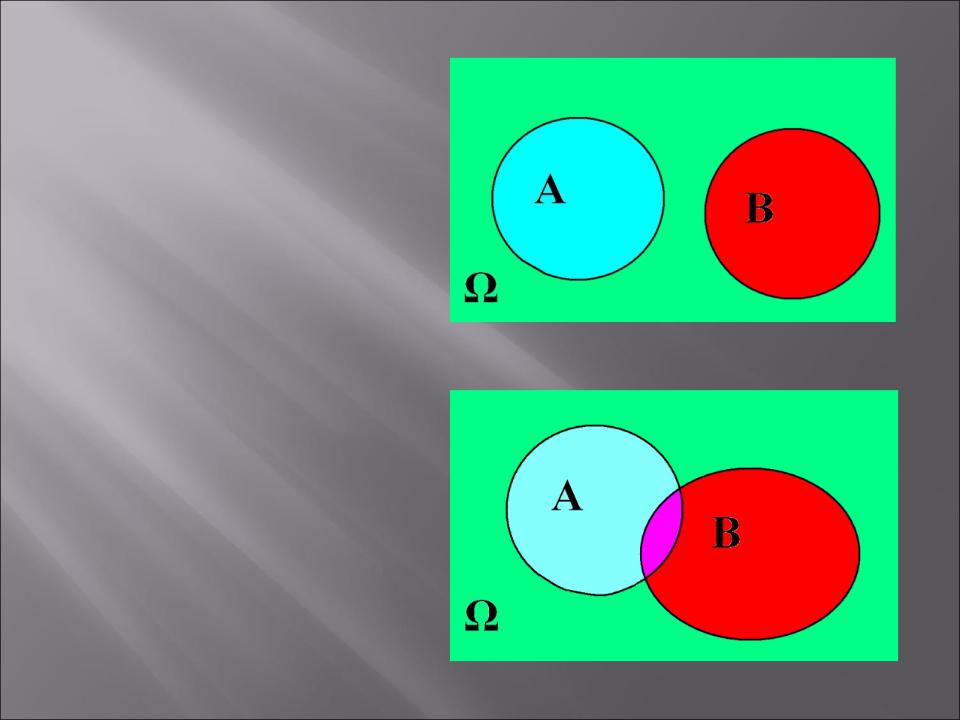
Несовместные
события
Совместные
события
Теорема 1 (для несовместных событий). Вероятность суммы двух несовместных событий равна в сумме вероятностей этих событий.
P(A B) P(A) P(B)
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
P(A B) P(A) P(B) P(A B)
Понятие независимости является центральным во всей теории вероятностей. Математически считают, что именно оно выделяет ее из общей теории меры и делает самостоятельной отраслью математической науки с необъятным полем для приложений.
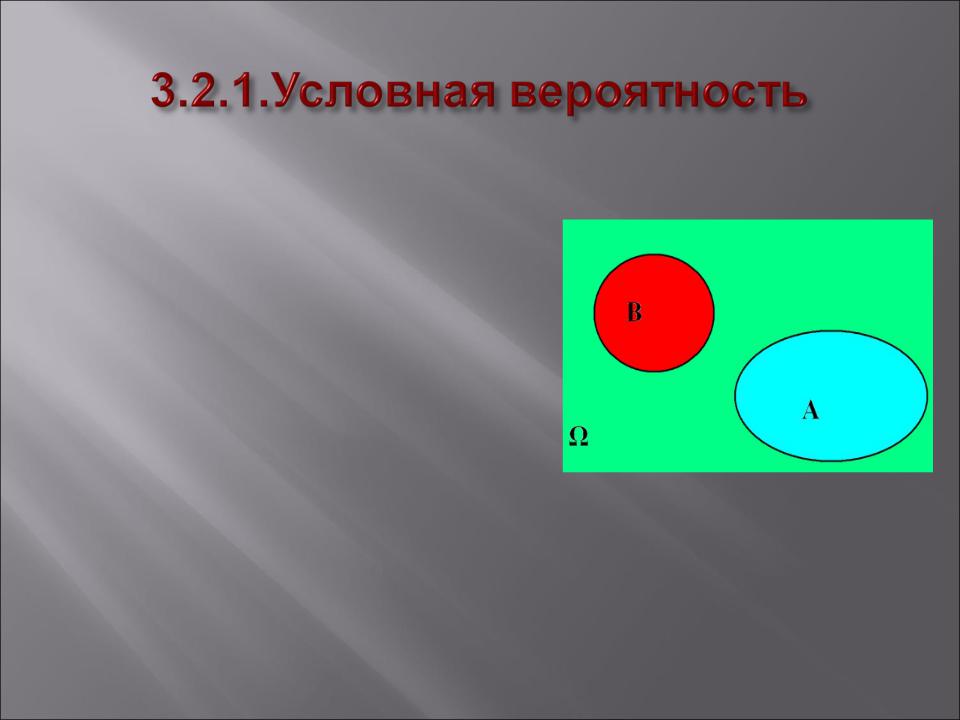
Пример 1. Пусть A и B
несовместны, и в результате эксперимента событие A произошло. Что
можно сказать о событие
B?
Событие B точно не произошло!
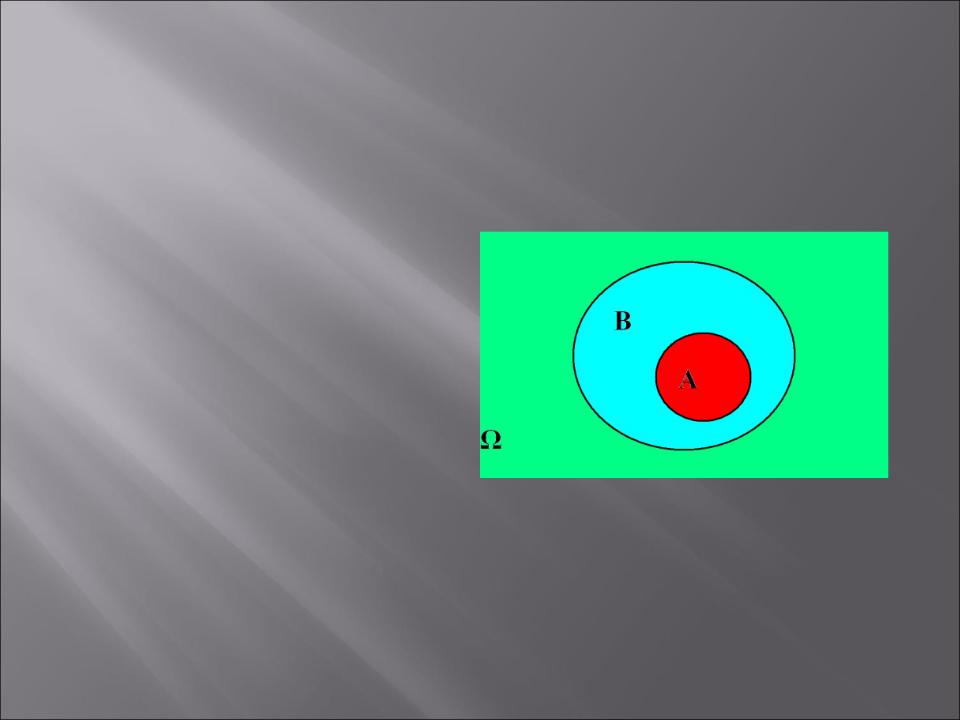
Пример 2. Пусть , A B в результате эксперимента событие A произошло. Что можно сказать о B?
Событие B точно произошло.
Теорема 1. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие произошло.
P(A) P(B/ A)
P(A B)
P(B) P(A / B)
Задача 1. Из полной игры домино дважды наудачу вынимают по одной пластинке, не возвращая их в игру. Найти вероятность того, что при первом извлечении появится не дубль, а при втором дубль.
Решение. A – «Появился не дубль» B – «Появился дубль»
Требуется найти вероятность события A и B.
P(A B) ?
Так как выбор производиться без возвращения, то события A и B – зависимы. Тогда:
Вычислим вероятности наступления этих
событий: P(A B) P(A) P(B / A)
Ответ: |
P(A) |
21 |
P(B) |
7 |
28 |
27 |
|||
|
|
|
|
P(A B) 2821 277 0,194