1.7. Зависимость теплового эффекта от температуры

Тепловой эффект процесса слабо зависит от давления и может существенно изменяться с температурой.

и.

Эти термодинамические соотношения определяют температурную зависимость теплового эффекта химических реакций и являются дифференциальными выражениеми закона Кирхгофа, одна из формулировок которого гласит:

Температурный коэффициент теплового эффекта равен изменению теплоемкости системы (или разности сумм теплоемкостей продуктов реакции и исходных веществ), происходящему в результате процесса.

Согласно представленным уравнениям, влияние температуры на тепловой эффект обуславливается знаками величин и .

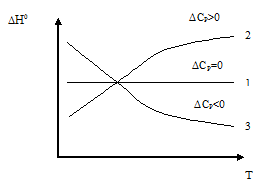
Проведем анализ зависимости (рис.4.):

1. ,, таким образом, тепловой эффект процесса не зависит от температуры;

2. , в этом случае тепловой эффект процесса с ростом температуры увеличивается;

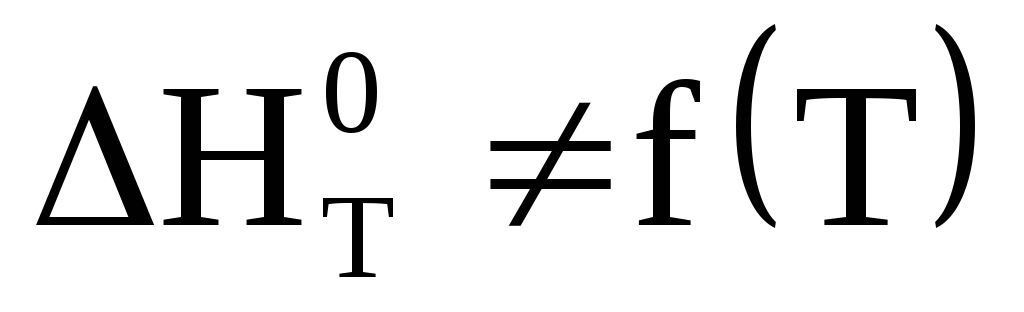3. , в этом случае тепловой эффект процесса с ростом температуры уменьшается.

Однако, нам необходимо знать каков тепловой эффект процесса при данной, конкретной температуре.

Интегрируя уравнения Кирхгофа и, получим выражения для расчета тепловых эффектов реакций при произвольных температурах:

V = const:

Р = const:

интегральная форма закона Кирхгофа

где ,– тепловые эффекты, осуществляемые в стандартных условиях при V,Р = const, которые рассчитываются по закону Гесса с использованием стандартных теплот образования веществ.

Если, например, и величина отрицательная, то графически зависимость теплового эффекта от температуры имеет вид (рис.5.):

Вобщем случае тепловой эффект при постоянной теплоемкости можно определить из уравнения:

Часто при проведении расчетов возникает необходимость учета температурной зависимости теплоемкости компонентов реакции. Как правило, аналитическая форма функциональной зависимости C = f(T)неизвестна.В этом случае обычно используют эмпирические соотношения в виде степенных рядов для отдельных компонентов реакции С =  + Т + Тⁿ, а затем уже рассчитывается температурная зависимость теплоемкости химической реакции. Тогда, зависимость теплоемкости от температуры приводится к виду

, гдеи т.д.

Подставляя это выражение в уравнения Кирхгофа, для стандартных условий, получим

.

После интегрирования уравнение приводятся к виду:

.

Если в рассматриваемом интервале температур имеют место фазовые переходы "твердое тело – жидкость", "жидкость – пар", то в уравнениях температурной зависимости теплового эффекта появляются дополнительные составляющие, учитывающие тепловые эффекты фазовых переходов:

.

– изменения изохорной и изобарной теплоемкостей в соответствующих фазовых состояниях (твердом, жидком и газообразном). Температурная зависимость энтальпии, с учетом фазовых переходов, качественно показана на рис.6.

По величине воспользовавшись соотношением Клаузиуса, можно рассчитать тепловой эффект процесса в изохорических условиях, т.е. приV=const:, гдеn – разность между числом молей газообразных веществ в конечном и начальном состояниях. (например, СО₂+С=2СО;n=2-1=1.

При n=0,.

2. Второе начало термодинамики. Энтропия.

Все процессы, происходящие в природе, отличаются определенной направленностью, т.е. они совершаются сами собой только в одном направлении, хотя первый закон не запрещает их протекания в обратном направлении.

Необходимо ввести критерии, позволяющие определить возможность и наиболее вероятное направление, а также пределы протекания самопроизвольных процессов.

Попытки найти такой критерий привели к предположению, что самопроизвольно осуществляются только экзотермические процессы. Однако, мы знаем, что многие спонтанные термодинамические процессы, в частности химические реакции, могут протекать как с поглощением теплоты

так и с ее выделение:

сопровождаясь возрастанием неупорядоченности систем (газ более разупорядочен, чем кристалл или жидкость).

Более того, многие реакции, например,

не протекают самопроизвольно, однако сопровождаются отрицательным изменением энтальпии. Поэтому – изменение внутренней энергии или энтальпии не может служить критерием, позволяющим предвидеть направление протекания процесса (реакции).

Критерии возможности направления протекания процесса определяет II закон термодинамики, который был сформулирован в 60-х годах прошлого столетия.

С его помощью решаются сформулированные выше два круга вопросов.

1. определяется возможность, направление и предел протекания термодинамического процесса в данной системе в заданных условиях.

2. устанавливаются параметры протекания термодинамического процесса в заданном направлении с необходимой полнотой.

Клаузиусом была введена функция, названная энтропией S, и сформулировано два принципа: принцип существования энтропии и принцип возрастания энтропии в изолированных системах.

Принцип существования энтропии

Для каждой термодинамической системы существует функция состояния системы S - энтропия, определяемая тем, что ее дифференциал (dS) при элементарном обратимом (равновесном) процессе равен отношению бесконечно малого количества теплоты (q), сообщенного системе, к абсолютной температуре системы:

.

Принцип возрастания энтропии

Энтропия изолированной системы при наличии в ней необратимых процессов всегда возрастает

.

Таким образом, в изолированной системе обратимые процессы протекают без изменения энтропии, а необратимые - с возрастанием энтропии.

Свойства энтропии

Энтропия– функция состояния системы. Ее изменение зависит от начального и конечного состояний системы.

Энтропияявляется мерой неупорядоченности системы..

Энтропия – аддитивная функция, т.е. энтропия системы равна сумме энтропий ее частей (это экстенсивный параметр!)

Энтропия– вероятностная функция. Она показывает вероятность процесса и направление наиболее его вероятного протекания:

, (уравнение Больцмана)

где W- термодинамическая вероятность;k– постоянная Больцмана. Термодинамическая вероятность – это число микросостояний, т.н. вариантов в расположении частиц (атомов молекул), которыми может быть осуществлено данное макросостояние.

Термодинамическую вероятность, которая может принимать очень большие значения, следует отличать от математической, всегда меньшей единицы.

Энтропия – мера рассеивания энергии в окружающую среду, т.е. та часть энергии, которая в полезную работу не превращается!!!

Все изложенное выше находит отражение в формулировках второго закона термодинамики:

1.Тепло не может самопроизвольно переходить от более холодного к более теплому телу (Клаузиус).

2.Невозможно создать вечный двигатель второго рода, т.е. такую тепловую машину, в которой бы теплота полностью переходила в работу.

3.Любая система, представленная сама себе, будет изменяться в направлении состояния, отвечающего максимальной вероятности (Льюс).

4. Энтропия изолированной системы увеличивается или остается постоянной

> для самопроизвольных необратимых процессов

= для обратимых процессов.

В последней четвертой формулировке заключен критерий самопроизвольности процессов в изолированных системах: спонтанно в такой системе могут протекать те процессы, которые сопровождаются увеличением энтропии (перемешивание газов, выравнивание температур и давлений).

1. расчет изменения энтропии в обратимых процессах

(равновесных процессах)

1. Нагревание веществ от Т₁ до Т₂ (неизотермический процесс)

Уравнения для вычисления S изобарного (P=const) и изохорного (V=const) нагревания 1 моля веществ имеют вид:

и .

Для n молей: и.

2. Изотермическое расширение газа, объем которого изменяется при некоторой температуре Т от V₁ до V_2:

.

Для n молей:

3. Изменение энтропии фазовых переходов вычисляется по уравнению

,

где - теплота фазового перехода,- температура фазового перехода.

Например, теплота фазового перехода воды из жидкого состояния в парообразное (процесс испарения) составляет около 41 кДж/моль. Следовательно, изменение энтропии составляет:

Дж/моль·К.

4. Изменение энтропии химических реакций, протекающих в изотермических условиях, вычисляется как разность сумм энтропий конечных и исходных веществ участвующих в реакции

.

,

где S_C, S_Д, S_A, S_B - абсолютные энтропии веществ - участников реакции; а, в, с, д - стехиометрические коэффициенты.

Абсолютные значения энтропий веществ вычислены для стандартных условий протекания реакций и представлены в термодинамических справочниках.

Определение абсолютных энтропий веществ стало возможным после формулировки постулата Планка, который позволил определить начало отсчета энтропии - состояния с минимальной энтропией при абсолютном нуле температуры.

Постулат Планка составляет содержание 3 - го закона термодинамики и формулируется так:

«Энтропия полностью упорядоченных кристаллических тел при температуре абсолютного нуля равна 0».

S_0К =0, тогда .

Стандартная энтропия индивидуальных веществ (S^o₂₉₈) имеют размерность Дж/мольК, т.е. это количество теплоты, которое рассеивается в окружающую среду, если моль вещества нагревается на 1^о.

Т. е. Энтропия индивидуальных веществ характеризует энергетически бесполезную теплоту; ту теплоту, которая в работу не переходит.

При расчетах S системы следует не забывать, что энтропии веществ - величины экстенсивные, т.е. зависящие от массы.

2. применение II закона термодинамика для неизолированных систем

Многие процессы химической технологии протекают при постоянном давлении и температуре, если они проводятся в открытых аппаратах, илипри постоянном объеме и температуре, если они проводятся в закрытых аппаратах, например, в автоклавах. В химической технологии о направлении процесса и равновесии в системе при постоянных давлении и температуре судят по энергии Гиббса или при постоянных объеме и температуре — по энергии Гельмгольца. Это связано с тем, что на практике рассмотрение изолированных систем и использование в качестве критерия равновесия и направления процесса крайне неудобно, так как рассмотрение изолированной системы часто встречает большие затруднения.

Изохорно-изотермические условия (V=const, T=const)

по уравнению Гиббса - Гельмгольца

.

При - самопроизвольный процесс возможен в прямом направлении; присистема находится в состоянии равновесия; присамопроизвольный процесс в прямом направлении невозможен, возможен обратный процесс.Таким образом, если в системе, находящейся при Т и V = const, происходит какой-либо неравновесный самопроизвольный процесс, то энергия Гельмгольца уменьшается до тех пор, пока система не достигнет равновесия.

Изобарно-изотермические условия (Р=const, T=const)

по уравнению Гиббса - Гельмгольца

.

При - самопроизвольный процесс возможен в прямом направлении; присистема находится в состоянии равновесия; присамопроизвольный процесс в прямом направлении невозможен, возможен обратный процесс.Таким образом, если в системе, находящейся при Т и V = const, происходит какой-либо неравновесный самопроизвольный процесс, то энергия Гельмгольца уменьшается до тех пор, пока система не достигнет равновесия.