8. Дифференциальные уравнения

231 – 240. Найти общее решение дифференциального уравнения.

231.	а) ;	б) .
232.	а) ;	б) .
233.	а) ;	б) .
234.	а) ;	б)
235.	а) ;	б) .
236.	а) ;	б)
237.	а) ;	б) .
238.	а) ;	б) .
239.	а) ;	б) .
240.	а) .	б) .

241. .	242. .
243. .	244. .
245. .	246.
247.	248.
249.	250.

251 – 260. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиямy(0) =y₀,y'(0)=y'₀. ( Задача Коша).

251. y'' – y' ;,.

252. y'' + y;y(0) = 4; ;

253. y'' +7y'+12y=;y(0) = 1,y'(0) = 1;

254. y'' –2y' = x²–1; y(0) = 1, y' (0) = 1;

255. y''- ;y(0) = 1, y' (0) = 1.

256. y'' + 9yy(0) = ;y' (0) = 0.

257. y'' – 4y' +8y ;y(0) = 2, y' (0) = 3.

258. y'' – 2y' =;y(0) = 2, y' (0) = 2.

259. y'' +2y' +10y;y(0) = 0, y' (0) = .

260. y''– 6y'+9y = ;y(0)=1,y'(0)=3.

261 – 270. Дана система линейных дифференциальных уравнений с постоянными коэффициентами

.

Найти общее решение системы.

261. ; 262. ;

263. ; 264. ;

265. 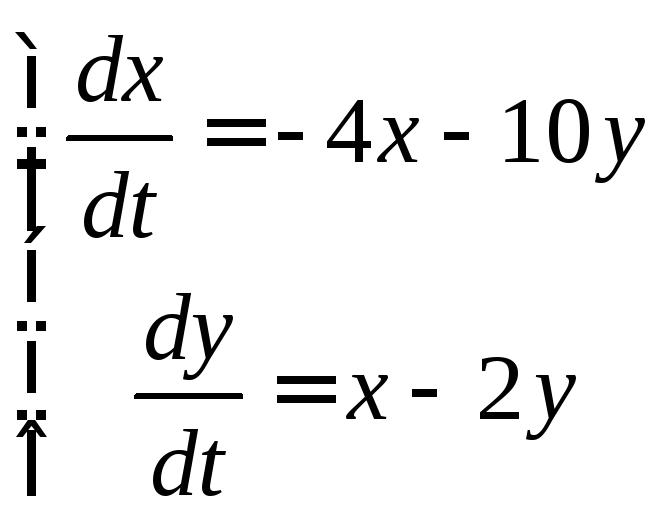; 266. ;

267. ; 268. ;

269. ; 270. ;

9. Кратные, криволинейные и поверхностные интегралы

271 – 280. Изменить порядок интегрирования.

271. ; 272..

273. ; 274..

275. ; 276..

277. ; 278..

279. ; 280..

281 – 290. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy.

281.	;	.
282.		.
283.	,	.
284.	,	.
285.	,	.
286.	,	.
287.		.
288.	,	.
289.	,	.
290.	,	.

291 – 300. Вычислить криволинейные интегралы. Сделать чертёж.

291. вдоль ломанойOBA, где 0(0,0)A(1,1).

292. где- дуга окружности.

293. где-дуга парболыот т.О(0,0) до т.В(1,2).

294. вдоль отрезкапрямой от точкиА(1,2) до точкиВ(2,4).

295. если.

296. если- окружность.

297. , где - дуга параболыот точкиА. (1,1) до точкиВ(2,8).

298. , где- дуга параболыот точкиО(0,0) до точкиА(1,2).

299. по контуру фигуры, ограниченной линиямив полажительном напровлении (против часовой стрелки).

300. , гдедуга Эллипса.

10. Ряды

301 – 310. Исследовать сходимость числового ряда .

301. ; 302. .

303. ; 304. .

305. ; 306.

307.; 308. .

309. ; 310..

311–320. Найти область сходимости ряда.

311. ; 312. .

313. ; 314. .

315.; 316.

317.; 318.

319.; 320..

321–330. Вычислить интеграл с точностью до 0.001, разложив подынтегральную функцию в степенной ряд .

321. ; 322. ;

323. ; 324.

325. 326. .

327. 328. .

329. 330.

331 – 340. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальному условию.

331.	.	332.
333.		334.
335.		336.
337.		338.
339.		340.

341 – 350. Разложить данную функцию f(x) в ряд Фурье в интервале [a;b].

341.		342.
343.		344.
345.		346.
347.		348.
349.		350.