5. Приложения дифференциального исчисления

151 – 160. Исследовать методами дифференциального исчисления функцию и, используя полученные результаты, построить её график.

151. . 152..

153. . 154..

155. . 156..

157. . 158..

159. . 160..

6. Дифференциальное исчисление функций нескольких переменных

161 – 170. Найти а) ; б).

161.	a),	б) .
162.	а) ,	б) .
163.	а) ;	б) .
164.	а) ;	б) .
165.	а) ;	б) .
166.	а) ;	б) .
167.	а) ;	б) .
168.	а) ;	б).
169.	а);	б).
170.	а) ;	б) .

171 – 180. Дана функция .

Показать, что .

171. .

172. .

173. .

174. .

175. .

176. .

177. .

178. .

179. .

180. .

181 – 190. Найти наименьшее и наибольшее значения функции в замкнутой областиD, заданной системой неравенств. Сделать чертеж.

181. ;

182.

183.

184.

185.

186.

187.

188.

189.

190.

191 – 200. Даны функция , точкаи вектор. Найти: 1) gradzв точкеА; 2) производную в точкеАпо направлению вектора.

191.

192.

193.

194.

195.

196.

197.

198.

199.

200.

7. НеопределЁнный и определЁнный интегралы

201 – 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.

201.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
202.	a);	б) ;
	в) ;	г) ;
	д) ;	е) .
203.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
204.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
205.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
206.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
207.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
208.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
209.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .
210.	a) ;	б) ;
	в) ;	г) ;
	д) ;	е) .

211 – 220. Вычислить несобственный интеграл или доказать его расходимость.

211.	а) ;	б). .
212.	а) ;	б). .
213.	а) ;	б). .
214.	а) ;	б). .
215.	а) ;	б). .
216.	а) ;	б). .
217.	а) ;	б). .
218.	а) ;	б). .
219.	а) ;	. б). .
220.	а) ;	б). .

221. Найти площадь фигуры, ограниченной параболой и прямой.

222. Найти площадь фигуры, ограниченной параболой и прямой.

223. Найти длину дуги данной линии

.

224. Вычислить объем тела, образованного вращением вокруг оси Oxкривой,x= –1,y= 0.

225. Вычислить площадь фигуры, ограниченной

226. Вычислить длину дуги данной линии

.

227. Вычислить объем тела, образованного вращением вокруг Oхкривой,x= 0,y= 1.

228. Найти длину кардиоиды .

229. Вычислить объем тела, полученного вращением вокруг оси Оyфигуры, ограниченной парабалами

230. Найти длину дуги полукубической парабалы , концами которой являются точки с абсциссамии.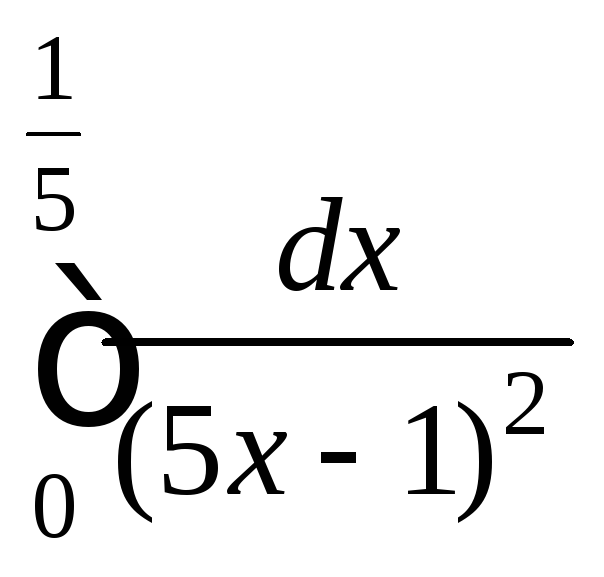