Шпоры по начерталке / Виды проекций

1.Виды проецирования. Образование ортогонального чертежа на одной, двух и трёх плоскостях проекций

Центральное проецирование. Основными видами проецирования являются центральное и параллельное. Центральное проецирование представляет собой общий случай проецирования геометрических образов из некоторого центра на плоскость.

Пусть задана плоскость П₁ и кривая линия k с точками А, В, С (рис.1).

Рис.1

Возьмем некоторую точку S, не лежащую в плоскости П₁. Через точку S и точки А, В, С кривой k проведем прямые до пересечения с плоскостью П₁ в точках A₁, B₁, C₁. Проведя таким образом через S и каждую точку кривой k прямые, получим в плоскости П₁ изображение k₁ кривой k.

В соответствии с описанным построением введем следующие понятия:

S - центр проекций; П₁ - плоскость проекций; кривая k с точками А, В, С - объект проецирования; SА, SВ, SС - проецирующие лучи; A₁,B₁,C₁ - центральные проекции точек А, В, С; k₁ - центральная проекция кривой k. Рассматривая каждую пространственную фигуру как совокупность точек, можно сказать, что проекция фигуры представляет собой множество проекций ее точек.

Свойства центрального проецирования:

1. Любая точка (кроме S) проецируется на плоскость проекций в единственную точку (рис.1).

2. Каждой точке (A, B, C, D,...), принадлежащей какой-либо линии (кривой или прямой), соответствует проекция (A₁, B₁, C₁, D₁, ...) этой точки на проекции данной линии (рис.1).

3. Кривая в общем случае проецируется в кривую, а прямая - в прямую. Если прямая совпадает с проецирующим лучом, например DE (рис.1), то она проецируется в точку D₁ E₁. Плоскость, проходящая через центр проекций, проецируется в прямую и называется проецирующей. Кривая, все точки которой принадлежат проецирующей плоскости, проецируется в прямую.

Рис11

4. Точка пересечения линий проецируется в точку пересечения проекций этих линий (рис.1).

Центральное проецирование обладает большой наглядностью и применяется в строительном черчении, в архитектуре, в живописи и т.п. Недостатком центрального проецирования является сложность построения изображения предмета и определения истинных размеров. Поэтому оно имеет ограниченное применение в техническом черчении.

рис12

П араллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления. Пусть требуется построить параллельную проекцию кривой k на плоскость П₁(рис.2).

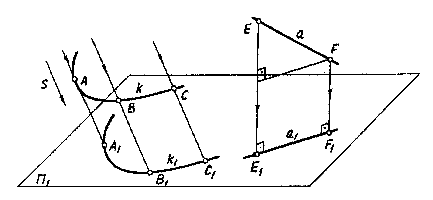
Спроецируем в направлении s все точки кривой k на плоскость П₁.Чтобы спроецировать точки указанной кривой, например А, В, С, нужно провести через них прямые, параллельные направлению s, до пересечения с плоскостью П₁. Точки пересечения A₁,B₁,C₁ проецирующих лучей с плоскостью П₁ и будут параллельными проекциями точек А, В и С. Таким образом можно построить проекции множества точек кривой k.

В зависимости от направления проецирования по отношению к плоскости проекций П₁ различают два вида параллельных проекций: косоугольную, когда проецирующие лучи не перпендикулярны к плоскости П₁ (рис. 2, кривая k), и прямоугольную (или ортогональную), когда проецирующие лучи перпендикулярны к плоскости проекций (рис.2, прямая а).

Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции, особенно ортогональные, обладают удобоизмеримостью и простотой построения. Поэтому ортогональное проецирование широко

распространено в технике и является основным методом начертательной геометрии.

Свойства параллельного проецирования

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Проекции параллельных прямых параллельны между собой, т.е., если, а b, то a₁ b₁. Пусть отрезки АВ и DE параллельны (рис. 3), тогда проецирующие плоскости AA₁BB₁ и DD₁E₁E будут также параллельны. Следовательно, линии A₁B₁ и D₁E₁ пересечения этих плоскостей с П₁ будут параллельны.

2.Отношение отрезков, принадлежащих параллельным прямым или одной прямой, равно отношению проекций этих отрезков, т.е., если AB DE, то AB / DE =  A₁B₁ / D₁E₁

3. При параллельном перемещении плоскости проекций проекция фигуры не изменяется. Если П₁П₂, то A₁B₁C₁ = A₂B₂C₂ (рис.4).

Рис.4 Рис.5

Свойства ортогонального проецирования

Наряду со свойствами параллельного (косоугольного) проецирования ортогональное проецирование имеет следующие свойства.

1. Отрезок прямой в общем случае равен гипотенузе прямоугольного треугольника, у которого один катет равен его проекции на данную плоскость проекции, а второй - разности расстоянии концов отрезка до этой плоскости (рис.5).

2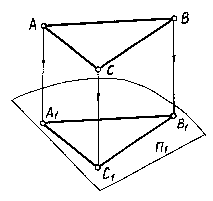. Любой отрезок прямой и плоская фигура, параллельные плоскости проекций, проецируются на эту плоскость без искажения (рис.6), например, если АВ  П₁, то A₁B₁ = AB ; ABC П₁, то A₁B₁C₁ = ABC.

Рис.6 Рис.7

3. Проекция любой фигуры (плоской фигуры, отрезка прямой и т.д.) не может быть больше самой фигуры (как следствие п.1 и 2).

4.Ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны, т.е., если a  b, и a  П₁, то a₁ b₁ (рис.1.7). Пусть дано a b. Построим проекцию a b на П₁. AA₁ П₁ (как проецирующий луч), следовательно, плоскость Г (AA₁ b) также перпендикулярна П₁. Прямая а перпендикулярна плоскости Г, так как она перпендикулярна двум прямым AA₁ и b, принадлежащим плоскости Г. Но a₁ a (a П₁) и, следовательно, a Г, откуда A₁ перпендикулярна любой прямой плоскости Г, в том числе и b₁. Отсюда справедливо, что a₁ b₁. Это доказательство относится как к пересекающимся прямым, так и к скрещивающимся. Как видно из чертежа, если с Г, а Г , то c₁ a₁.

Образование ортогонального чертежа на одной, двух и трёх плоскостях проекций

Построим ортогональную проекцию предмета, изображенного на рис.8, на плоскость П₁. На этом чертеже можно измерить длину и ширину предмета, а высоту указать с помощью числа (в данном случае 30 мм). Такой чертеж носит название проекции с числовыми отметками. Способ проекций с числовыми отметками применяют при изображении пространственных форм, у которых одно измерение (в вертикальном направлении) очень мало по сравнению с большой протяженностью по двум другим направлениям, в том числе и в химии.

Если в предмет внести изменения, например, сделать вырез (рис.9), то для того, чтобы представить предмет в пространстве, предмет проецируют на две взаимно перпендикулярные плоскости проекций.

Вначале рассмотрим построение проекций точки на плоскости П₁ и П₂. П₁ принято располагать горизонтально (рис.10) - ее называют горизонтальной плоскостью проекций. П₂ - вертикально, параллельно плоскости чертежа. Такую вертикальную плоскость называют фронтальной плоскостью проекций. Эти плоскости проекций пересекаются по линии Х, называемой осью Рис.9 проекций.

В системе двух взаимно перпендикулярных плоскостей проекций:

- горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций;

- фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.

Плоский чертеж можно получить путем вращения одной из плоскостей проекций вокруг оси проекций Х до совмещения со второй плоскостью. Например, вращением плоскости проекций П₁ вокруг оси Х можно совместить ее с плоскостью проекций П₂ (рис.11).

Плоский чертеж, состоящий из двух (или более) взаимосвязанных проекций, называют комплексным чертежом или эпюром (эпюр Монжа).

Аналогично можно построить две проекции предмета, изображенного на рис.9. На рис.12- комплексный чертеж. На таком чертеже на фронтальной плоскости хорошо видна форма выреза.

Введем в систему П₂, П₁ третью вертикальную плоскость проекций (рис.13), перпендикулярную оси х и, следовательно, горизонтальной и фронтальной плоскостям проекций. Ее называют профильной плоскостью проекций и обозначают П₃. Линии пересечения профильной плоскости проекций с горизонтальной и фронтальной плоскостями называют осями у и z. Точка О - пересечение всех трех осей проекций.

Рис 13 Рис14

Рассмотрим построение трех проекций некоторой точки А пространства. Спроецируем эту точку на плоскости проекций. Перпендикуляры, опущенные из точки А, пересекают: II₁ в точке A₁, II₂ - в А₂ и П₃ в А₃ - ортогональных проекциях точки А (рис.13).

Комплексный чертеж точки А получим, совместив плоскости II₁ и П₃ с плоскостью П₂ путем вращения плоскости П₁ вокруг оси х, а плоскости П3 вокруг оси z в направлениях, показанных стрелками на рис.13.

На комплексном чертеже, состоящем из трех проекций, проекции одной и той же точки лежат на линиях связи, перпендикулярных соответствующим осям проекций, т.е. A_lA₂-x, A₂A₃Az (рис.14).

Расстояния точки А до плоскостей П₁П₂.П₃ представляют собой координаты точки А: Х (отрезок АА₃), Y (отрезок AA₂) и Z (отрезок AA₁)(рис.13). На комплексном чертеже этих отрезков нет, но есть отрезки, равные им (см.рис.14).

АА₃ = A₁A_y = A₂A_z = X;

АА₂ = А₁,А_х, = А₃,А_z, = Y;

AA₁ = A₂A_x = А₃А_у = Z.

Рис. 15

Рассмотрим построение третьей (профильной) проекции по двум заданным. Пусть заданы две проекции А₁ и A₂ и оси проекций x, y, z (рис.14). Искомая проекция А₃ должна лежать на линии связи A₂A₃z. Из рис.13 видно, что расстояние проекции А₃ от оси z является координатой Y точки А, которая равна также расстоянию от A₁ до оси х. Отложив координату Y на линии связи А₂А₃, получим проекцию А₃ (рис14).

Аналогично строим три проекции предмета с наличием прорези. Комплексный чертеж такого предмета представлен на рис.15, на котором выявлены форма и размеры всех его элементов.