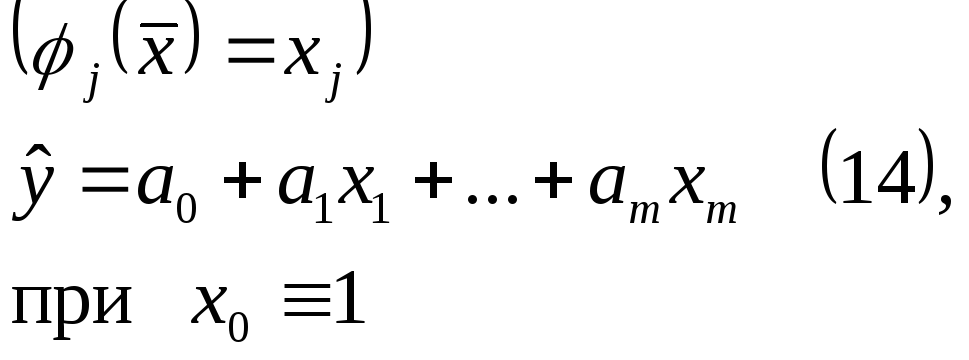Тема 07 (часть 1). Построение эмпирических статистических моделей хтп

§1. Постановка задачи.

Эти модели применяются, когда либо нет информации о механизме протекающих процессов, либо они плохо поддаются описанию с использованием физико-химических блочных моделей. В этом случае объект (химико-технологический процесс) представляется в виде "чёрного ящика" - кибернетической системы, в которой единственно доступной информацией являются её входные и выходные переменные:

где - вектор входных переменных, влияющих на состояние системы и её свойства,

- вектор выходных переменных, характеризующих состояние системы.

В общем случае строятся эмпирические модели для каждой отдельной выходной переменной из всех y_i ( i = 1,… ) в зависимости от всех входных переменных x_i ( i = 1,…m ), т.е.

где - (m + 1) коэффициентов эмпирической модели.

Конкретный вид функциональной зависимости (f) и значения коэффициентов определяются из опытных данных, т.е. эмпирически.

Так как результаты опытных измерений являются случайными величинами, то для их обработки используется один из наиболее распространённых методов математической статистики – метод регрессионного и корреляционного анализа.

В соответствии с методом регрессионного анализа y считается случайной величиной, распределённой по нормальному закону распределения, а компоненты вектора - детерминированными (неслучайными) величинами.

Поэтому согласно закономерностям теории вероятностей при каждом фиксированном значении вектора величина Y является случайной величиной с определённым (зависящим от ) условным распределением вероятностей.

В связи с этим для нормального закона распределения Y (допущение регрессионного анализа) для описания функции (1) используется зависимость условного математического ожидания от , которая называется уравнением регрессии:

Коэффициенты уравнения называются теоретическими коэффициентами регрессии.

Так как коэффициенты определяются по ограниченной выборке экспериментальных данных, то их значения отличаются от истинных (теоретических) и обозначаются (выборочные коэффициенты регрессии). В результате пользуются приближённым уравнением регрессии, в котором вместо условного математического ожидания фигурирует оценка и выборочные коэффициенты регрессии :

Для приближённого уравнения регрессии эмпирической статистической модели на выборке экспериментальных данных необходимо решить три основные задачи:

А)определить конкретный вид функции (3), т.е. решить задачу структурной идентификации;

Б)определить выборочные (эмпирические) коэффициенты регрессии , т.е. решить задачу параметрической идентификации;

В)провести статистический (регрессионный) анализ полученных результатов с целью оценки погрешностей полученной модели.

§2. Построение эмпирических моделей по данным пассивного эксперимента

2.1. Определение вида приближённого уравнения регрессии

В общем случае необходимо анализировать графики зависимостей экспериментальных данных выходных переменных y от входных x и по их виду выбирать конкретную форму функциональной зависимости (3).

Преобразование системы координат y – x даёт возможность выбрать оптимальный вид функциональной зависимости (3).

Для случая одной входной переменной х по опытным данным рекомендуется построить эмпирическую линию регрессии (рис.1) и с её помощью выбирать конкретный вид функции (3).

Изображение эмпирической линии регрессии:

При этом весь диапазон изменения x (рис.1) разбивается на s равных интервалов Δx. Все точки, попавшие в данный интервал Δx_j , относят к его середине x_j^* . После этого подсчитывают частные средние y_j^* для каждого интервала:

где n_j – число точек в интервале Δx_j.

В результате объём выборки определяется по формуле:

Эмпирическая линия регрессии y по x получается в виде ломанной линии путём последовательного соединения отрезками прямой линии точек:

При выборе вида функции (3) для случая нескольких входных переменных

может быть применён метод Брандона, который здесь не рассматривается.

В общем случае различают два вида уравнений регрессии (эмпирических моделей) – нелинейные по параметрам , статистический анализ которых осуществляется методом «нелинейной регрессии» и линейные по параметрам , статистический анализ которых проводится методом «линейной регрессии».

Линейные по параметрам модели могут быть представлены в следующем виде:

где - линейные или нелинейные функции входных переменных ().

Определение параметров (коэффициентов) линейных моделей и их регрессионный анализ существенно проще, чем для нелинейных моделей.

Поэтому нелинейные модели, по возможности, стараются линеаризовать и привести к виду (6).

Частными случаями уравнения линейной регрессии являются:

А)полиномиальная регрессия, когда

и её разновидности – линейная регрессия от одной переменной ( m=1 ):

и параболическая регрессия ( m=2 ):

Б)трансцендентная регрессия и её разновидности в виде зависимости показательного типа:

которая линеаризуется логарифмически:

и дробно-показательного типа:

которая также линеаризуется логарифмически:

В)множественная регрессия, когда число входных переменных больше 1: