
- •1. Основные допущения:
- •2. Особенности модели:
- •§ 1. Фазовое равновесие жидкость-пар.
- •1.1. Математическое описание процесса для многокомпонентной системы
- •1.2. Информационная матрица системы уравнений математического описания.
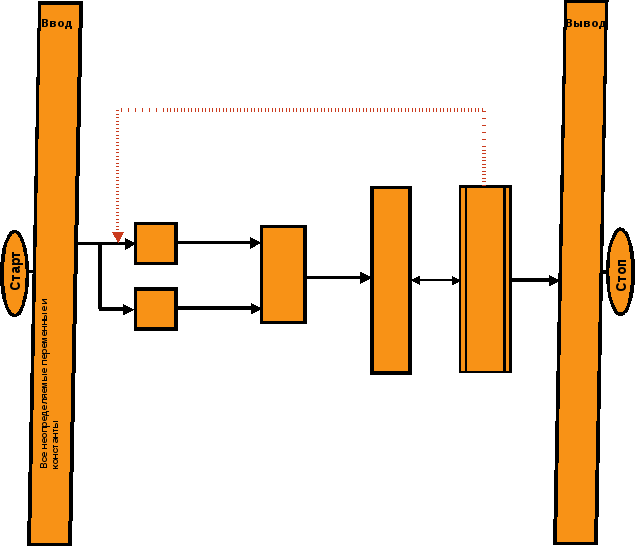
- •1.3. Блок-схема алгоритма расчёта.
- •§ 2. Многокомпонентная массопередача на тарелке с учётом гидродинамики движущихся потоков.
- •2.1. Основные допущения:
- •2.2. Математическое описание процесса массопередачи на тарелке.
- •§ 3. Компьютерная модель стационарного режима процесса непрерывной многокомпонентной ректификации в тарельчатой колонне.
- •3.1. Математическое описание процесса
- •3.2. Информационная матрица
- •3.3. Блок – схема алгоритма расчёта стационарного режима тарельчатой ректификационной колонны bp (bubble point) методом
- •3.4. Информационная матрица системы уравнений.
- •§4. Определение составов дистиллята ( ) и кубового продукта ( ) для простой ректификационной колонны с одним конденсатором (дефлегматором) и кипятильником.
1.2. Информационная матрица системы уравнений математического описания.
![]()
![]()
Результат решения уравнения: Т* - равновесная температура или температура кипения смеси.
При
этой температуре определяются равновесные
концентрации
![]() из уравнения (1):
из уравнения (1):
![]()
Для
идеальной жидкой фазы
![]() ( j=
1,…n
)
( j=
1,…n
)
![]()
Для идеальной жидкой и паровой фазы константа фазового равновесия определяется:
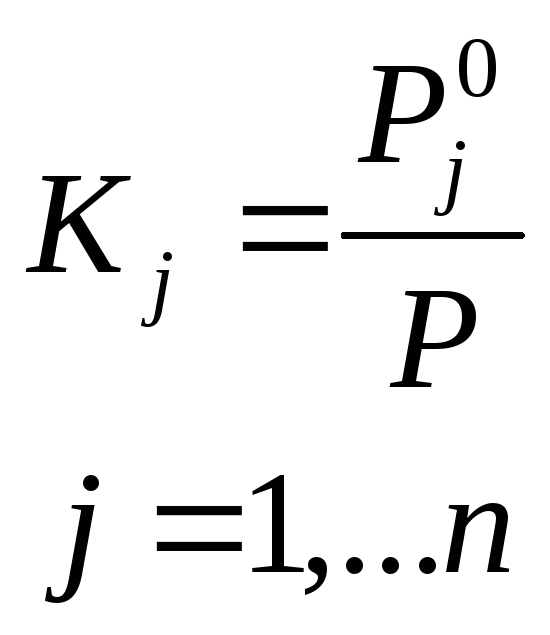
и зависит только от температуры, так как в соответствии с уравнением
Антуана
![]() зависит только от температуры.
зависит только от температуры.
В результате равновесный состав паровой фазы определяется по формуле:
![]()
1.3. Блок-схема алгоритма расчёта.
§ 2. Многокомпонентная массопередача на тарелке с учётом гидродинамики движущихся потоков.
2.1. Основные допущения:
стационарный режим;
движение потока жидкости может быть представлено моделью идеального смешения, а пара – идеального вытеснения;
на тарелке только многокомпонентная массопередача;
перекрестными эффектами матрицы коэффициентов массопередачи можно пренебречь;
потоки жидкости (L) и пара (V) на тарелке – константы.
2.2. Математическое описание процесса массопередачи на тарелке.
Уравнения для жидкой фазы:
![]()
![]()
Уравнения для паровой фазы:
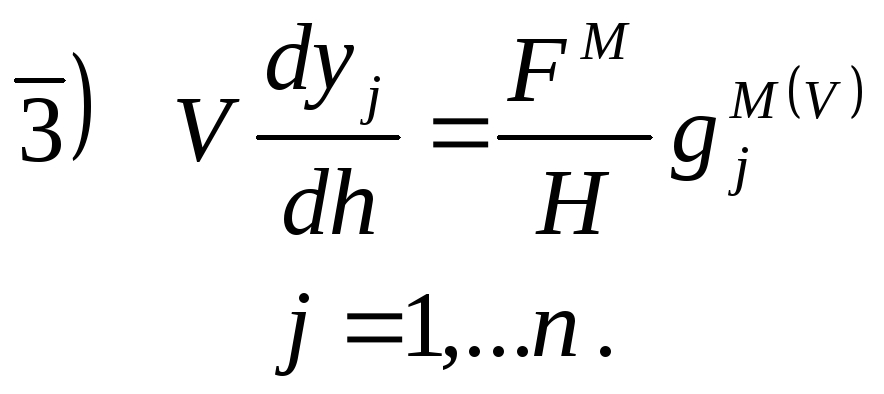
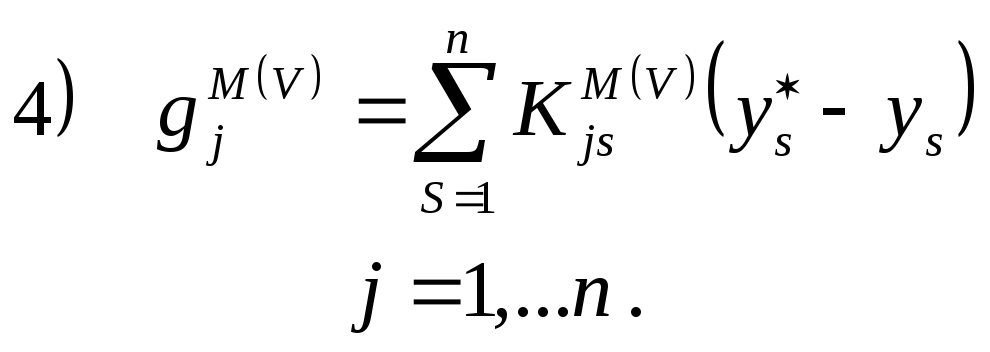
Для ректификации справедливо:
![]()
Для
определения
![]() в
уравнении (1) воспользуемся последним
соотношением:
в
уравнении (1) воспользуемся последним
соотношением:
![]()
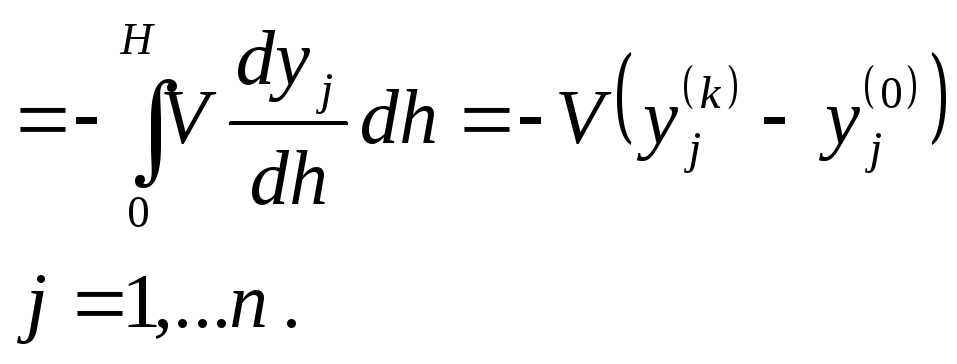
Подстановка в уравнение (1) приводит к уравнению покомпонентного баланса:
![]()
Далее воспользуемся уравнением локальной скорости многокомпонентной массопередачи из таблицы интенсивности источников массы и тепла в терминах паровой фазы (4):
![]()
где
![]() - равновесный состав паровой фазы.
- равновесный состав паровой фазы.
и представим её в матричной форме:
![]()
Недиагональные элементы матрицы коэффициентов массопередачи называются её перекрестными эффектами, и они на 2 – 3 порядка меньше диагональных элементов.
Поэтому ими пренебрегают. Матрица коэффициентов массопередачи становится диагональной:
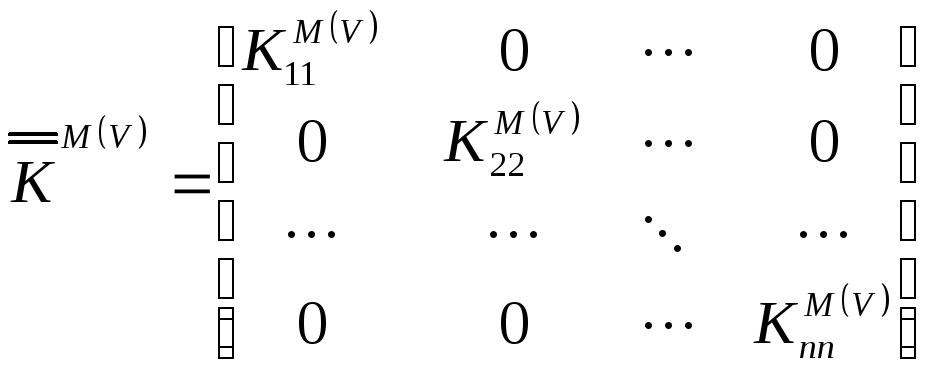
В результате уравнение (4) для локальных скоростей массопередачи принимает вид:
![]()
Система уравнений, описывающая многокомпонентную массопередачу на тарелке, может быть представлена в виде 3n уравнений:
![]()
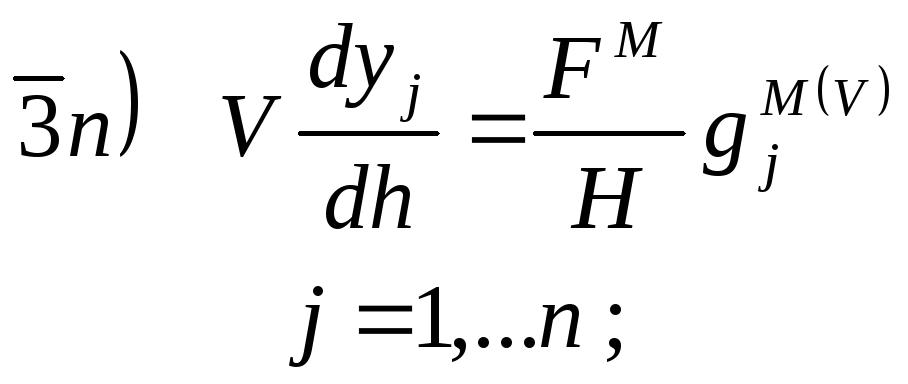
![]()
Подставляя последнее выражение в предыдущее, получается система 2n интегро-дифференциальных уравнений:
![]()
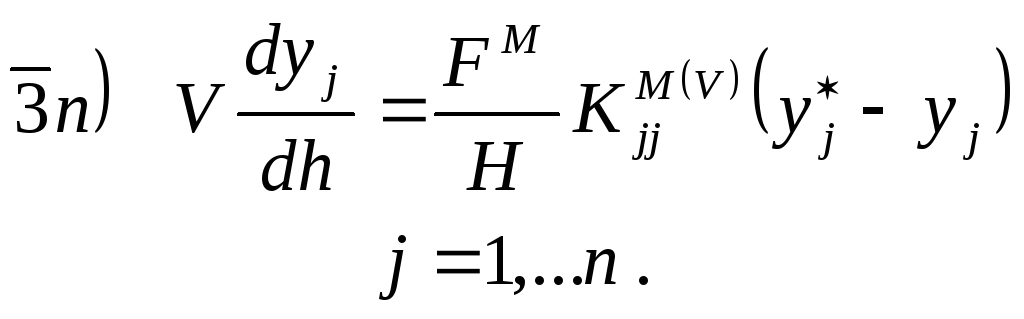
Аналитическое
решение дифференциального уравнения
![]() :
:
![]()
![]()
![]()
![]()
Для определения эффективности тарелки запишем:
![]()
С![]() учётом предпоследнего равенства
эффективность тарелки по компоненту
может быть определена:
учётом предпоследнего равенства
эффективность тарелки по компоненту
может быть определена:
а состав паровой фазы, покидающей тарелку с учётом предыдущих соотношений, учитывающих многокомпонентную массопередачу, рассчитывается по формуле:
![]()
где
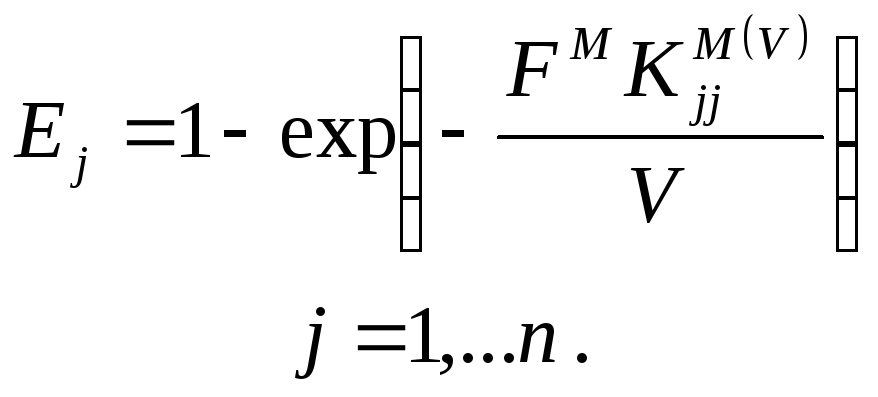
Для
теоретической тарелки Ej
= 1 и
![]()
В результате математическое описание процесса массопередачи на тарелке имеет вид:
Уравнение для жидкой фазы:
![]()
Уравнение для паровой фазы:
![]()
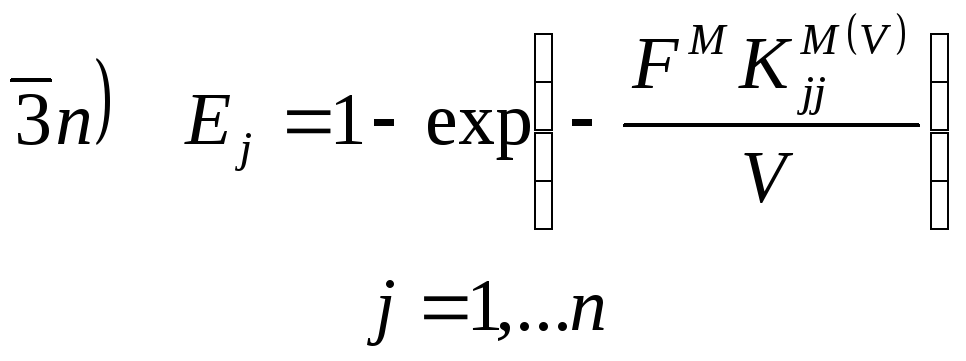
![]()
При условии идеальности паровой и жидкой фаз:
![]()
В этом случае давление насыщенного пара индивидуального вещества определяется по уравнению Антуана:
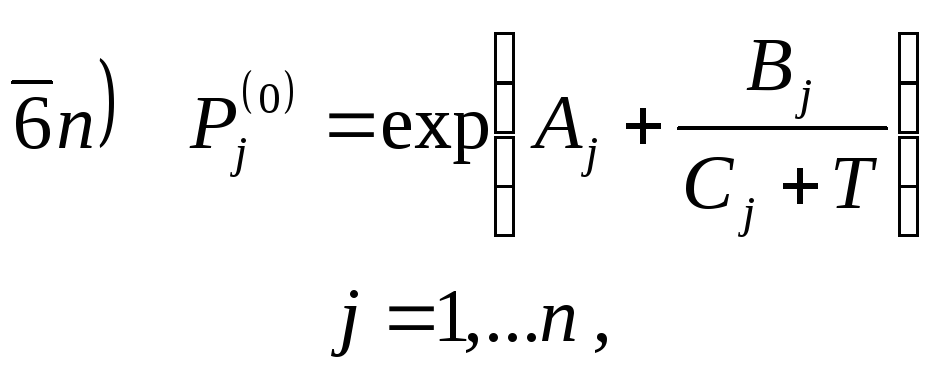
где
![]() - известные константы.
- известные константы.
