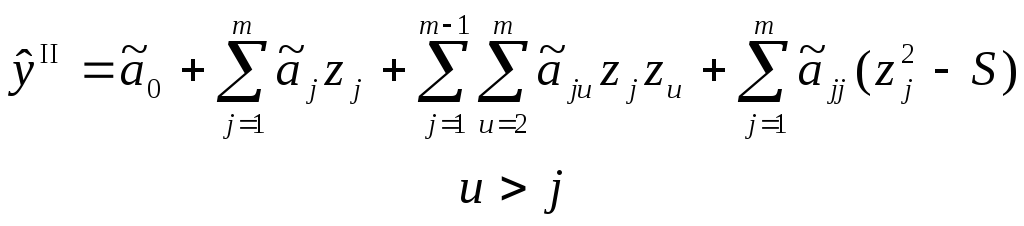3.3. Уточнение положения экстремума в почти стационарной области.
Для определения (уточнения) оптимальных величин факторов, обеспечивающих экстремальное значение выходной переменной у , решается система уравнений, которая вытекает из необходимого условия экстремума функции многих переменных:
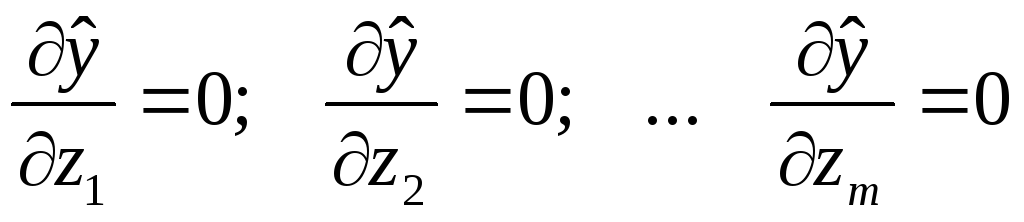
В данном случае также удобнее пользоваться кодированными факторами zj.
Для описания области, близкой к экстремуму, можно использовать уравнение второго порядка с двойными взаимодействиями факторов:
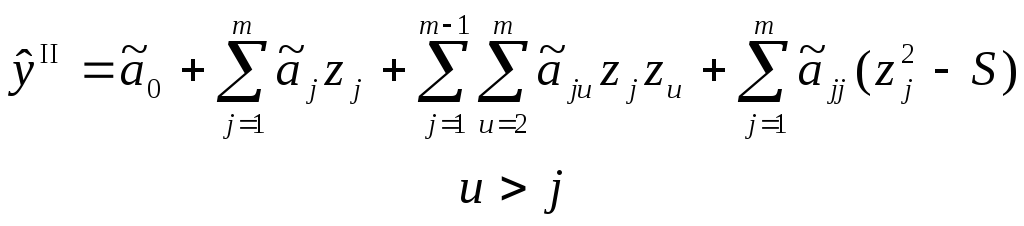
Введение величины S обеспечивает ортогональность матрицы эксперимента, который
проводится с целью
определения коэффициентов (
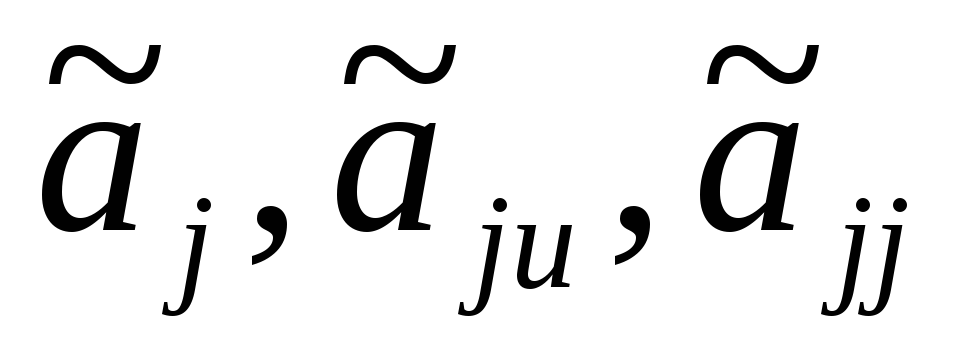) этой модели.
Для вычисления
коэффициентов уравнения для
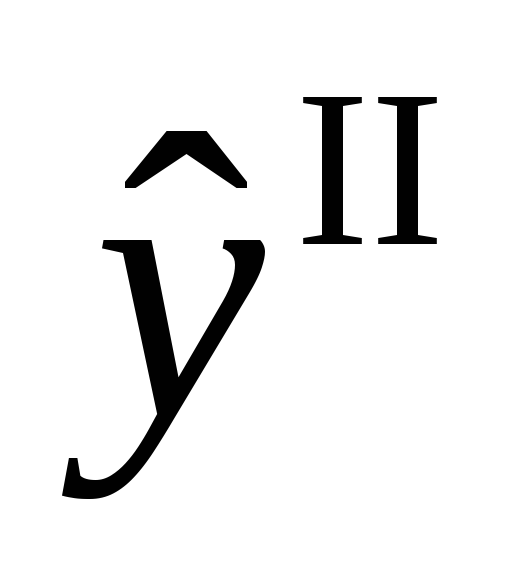реализуется ОЦКП эксперимента в почти
стационарной области.
Результат решения задачи уточнения положения экстремума нельзя считать удачным, если не выполняется условие:
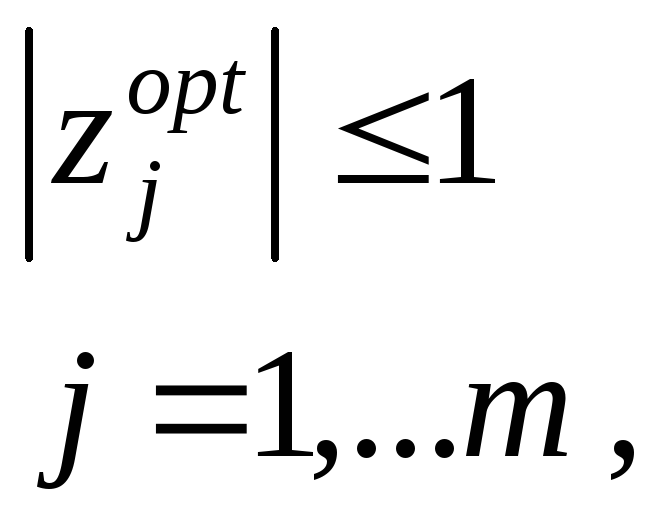
т.к. уравнение регрессии справедливо только в диапазоне кодированных факторов
(
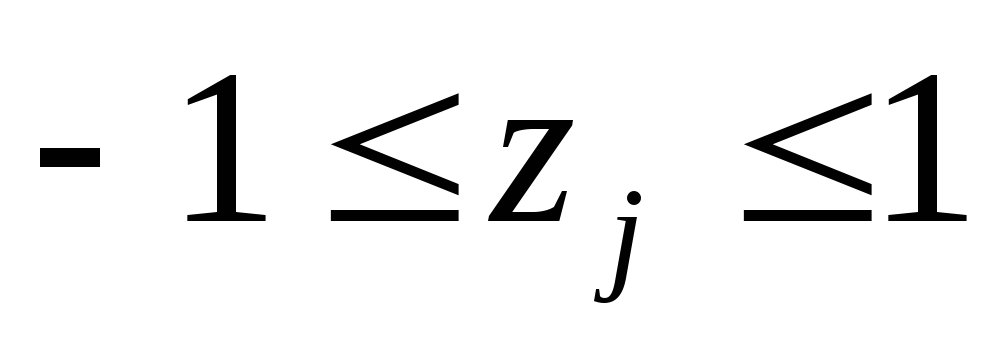), где был поставлен эксперимент.
При невыполнении этого условия рекомендуется снова реализовать ОЦКП эксперимента с
новым центром
плана, в частности в точке
.
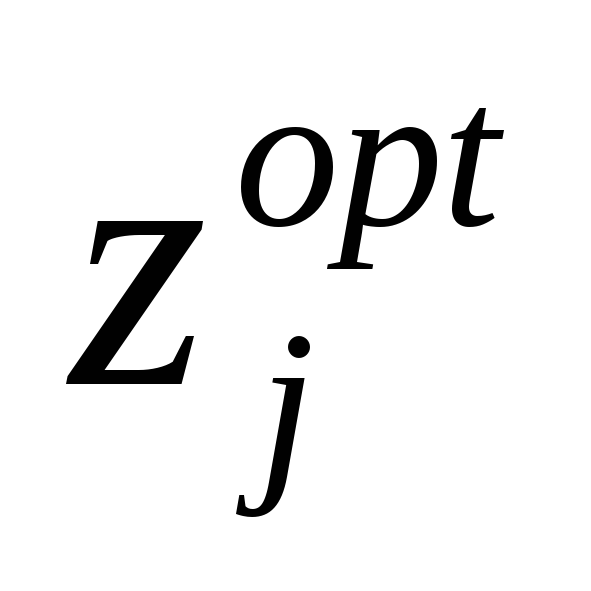Эту процедуру последовательного экспериментирования в окрестности экстремума рекомендуется продолжать до тех пор, пока условие приведённого выше неравенства не выполнится.
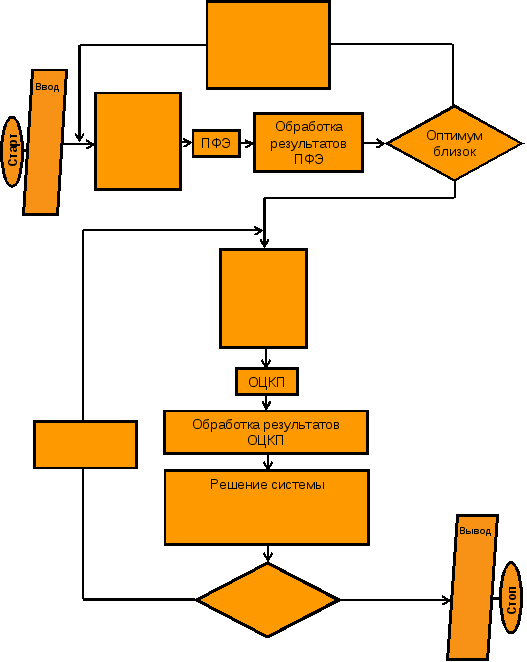
§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.
