Вернуться к списку лекций

Тема 02. Блочный принцип построения математического описания блочно-структурных физико-химических моделей

Оглавление

§1. Общие принципы построения структурной модели

§2. Анализ системы уравнений математического описания

2.1. Уравнения балансов гидродинамических моделей

2.1.1. Уравнения покомпонентного баланса

2.1.2. Уравнения общего баланса массы

2.1.3. Уравнения теплового баланса

2.2. Основные интенсивности источников элементарных процессов в потоках

2.3. Условные обозначения

§3. Математическое описание зоны идеального перемешивания (объекта с сосредоточенными параметрами).

3.1. Описание динамической модели

3.2. Описание статической модели

§4. Математическое описание зоны идеального вытеснения (объекта с распределёнными параметрами).

4.1. Описание динамической модели

4.2. Описание статической модели

Задания для самоконтроля

§1. Общие принципы построения структурной модели

1. Движущийся поток рассматривается как многофазная, многокомпонентная система (число компонентов = n), для каждой из фаз которой записывают уравнения балансов, базирующиеся на принятой гидродинамической модели движения потока: модель идеального смешения (МИС) и идеального вытеснения (МИВ) – крайние случаи.

2. Реальный поток движущейся фазы может быть представлен в виде комбинированной гидродинамической модели, состоящей из зон ИВ или ИС, причём для каждой зоны записывается своя система уравнений балансов.

3. Для каждой зоны записываются следующие уравнения балансов:

• Уравнение покомпонентных балансов, которое характеризует изменение концентраций компонентов в зоне; число уравнений - n

• Уравнение общего материального баланса, характеризующее изменение расхода потока в зоне; число уравнений -1

• Уравнение теплового баланса, которое характеризует изменение температуры в зоне; число уравнений -1

• Уравнение баланса импульса (количества движения), которое характеризует изменение давления в зоне (в этом курсе не используются).

Балансовых уравнений:

4. Если уравнения балансов включают производные по времени, то строятся динамические математические модели, которые описывают нестационарные режимы движения потока фазы. Если в системе уравнений нет производных по времени, то строятся статические математические модели, которые описывают стационарные режимы движения потока.

5. Основу уравнений математического описания составляют гидродинамические уравнения балансов для движущихся потоков, перечисленные в п.3, в которые включаются интенсивности источников вещества (компонентов) - в уравнения покомпонентных и материального балансов, а также интенсивности источников тепла - в уравнения теплового баланса.

6. Интенсивности источников веществ характеризуют скорости образования или расходования компонентов в потоке за счёт других отличных от гидродинамики элементарных процессов.

7. Интенсивности источников тепла характеризуют скорости выделения или поглощения тепла в потоке за счет также других элементарных процессов.

8. К основным элементарным процессам относятся:

- Химические превращения или реакции

- Массопередача

- Изменение агрегатного состояния или фазовые переходы

- Скорость потока подпитки

- Скорость теплопередачи

- Скорость теплоизлучения

ИТОГО:

i - 1,…n

9. Суммарные источники веществ определяются как аддитивная сумма

Для совмещённых процессов в этих суммах присутствуют два и более слагаемых, например: хемосорбция – массопередача и химическая реакция.

10. Различают объёмные интенсивности источников элементарных процессов, для локальных интенсивностей которых записываются физико-химические зависимости с соответствующими коэффициентами и поверхностные интенсивности источников элементарных процессов, для которых также записываются физико-химические зависимости с соответствующими

коэффициентами.

Например:

Химическая реакция:

- локальная скорость химической реакции по компоненту i (скорость, отнесённая к единице объёма).

- локальная скорость выделения или поглощения тепла за счёт химической реакции.

Массопередача

- вектор локальных скоростей массопередачи, отнесённых к единице поверхности

- поверхность массопередачи

11. Записываются выражения для локальных интенсивностей элементарных

процессов, зависящие от различных переменных процесса:

Химическая реакция:

где

П - произведение

если i - реагент

если i - продукт или отсутствует

( j = 1,…m )

Массопередача

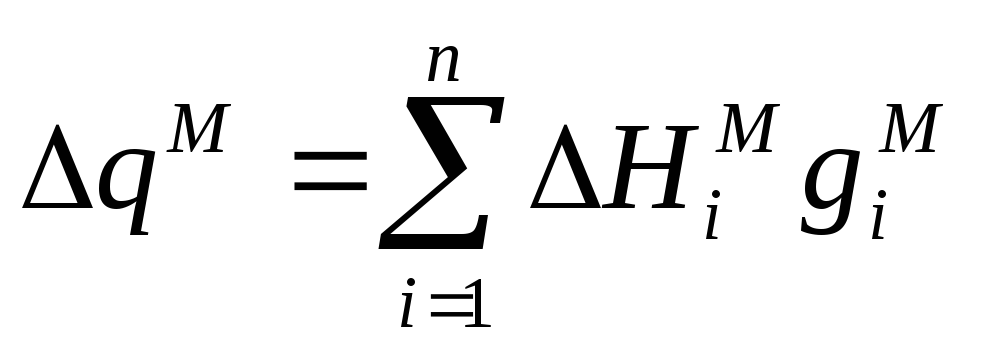
12. Записываются выражения для коэффициентов элементарных процессов, зависящих от различных переменных процесса (коэффициентов теплопередачи К^Т, констант скоростей реакций k_j и т.д.).

13. Записываются уравнения ограничений на конструкционные параметры протекающих процессов, например, длина трубы от 0 до L (где L - длина зоны) и на физические переменные процесса (например, сумма долей компонентов реакции).

В результате получаются уравнения математического описания или система уравнений МО процесса.

Оглавление