Лабораторные работы / Работа 3 - Тамбовцев - Сизов - 2006 / л3- ПРОСТАВЬ ВСЕ МОДУЛИ!!!!!!!!!

РОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

им. Д.И.Менделеева

Кафедра информатики и компьютерного моделирования

Обработка данных пассивного эксперимента.

выполнил

Студент группы Ф-32

Сизов А.П.

Проверил

Преподаватель

Тамбовцев И.И.

Москва 2006

T	20	28	43	49	58	73	83	93	98	110
P	938026	9,00658	8,59133	8,47418	8,3162	8,09029	7,95575	7,82911	7,76788	7,62419

Зависимость номер 1

После логарифмирования данная зависимость принимает вид:

Если и , тогда уравнение примет вид:

Составим систему уравнений:

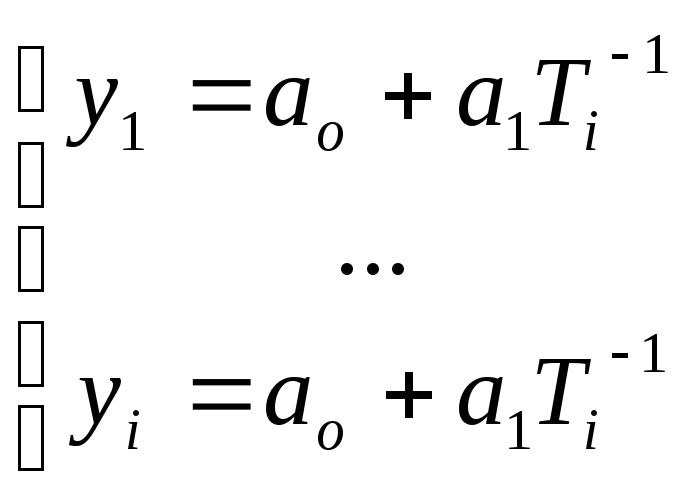
В матричной форме:

, если , тогда

Где матрицы принимают вид:

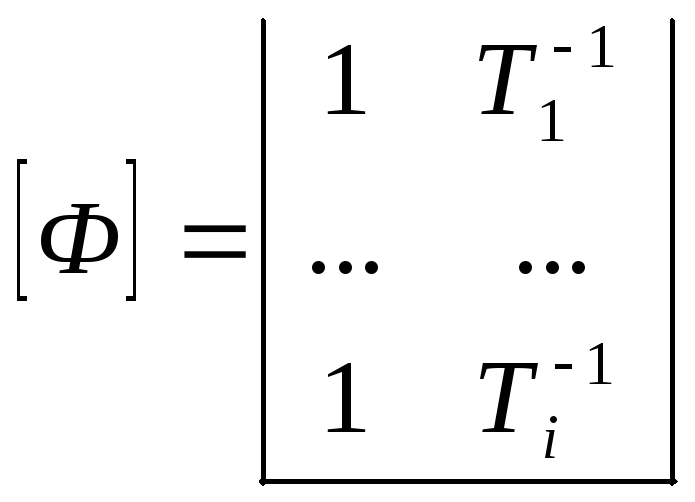
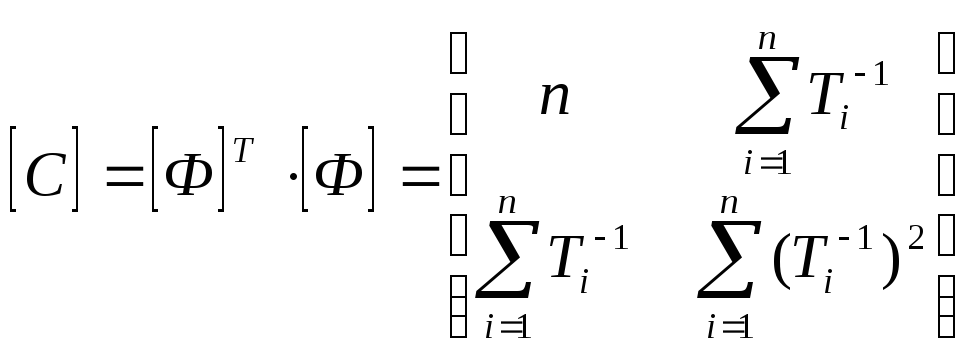
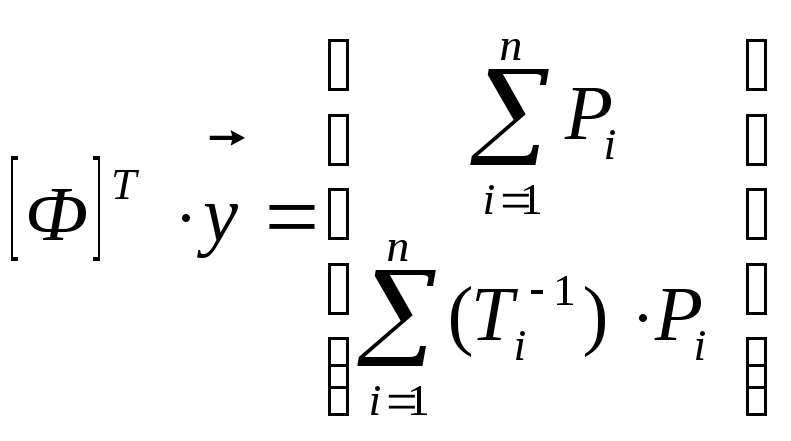
В результате решения системы получены следующие значения коэффициентов регрессии:

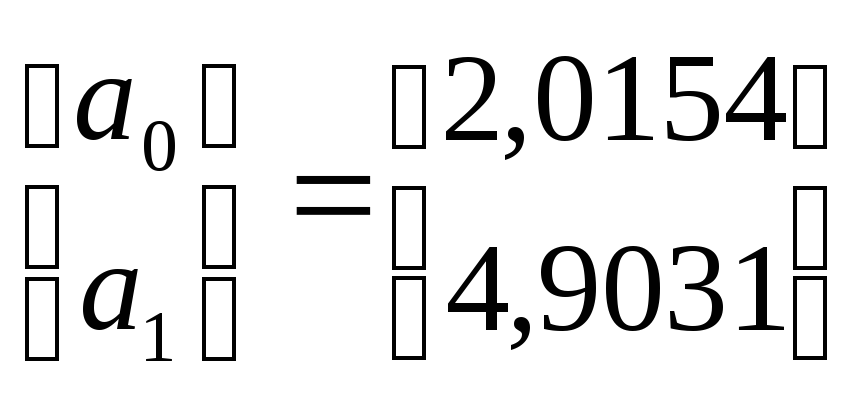
Проверим значимость коэффициентов уравнения регрессии и адекватности уравнения по критерию Фишера

0,0045

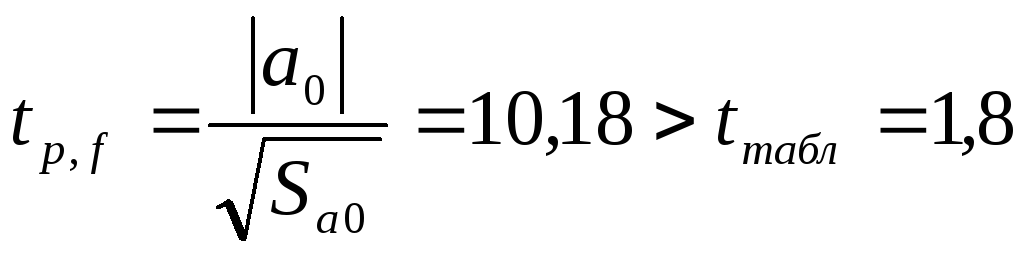– коэффициент значимый

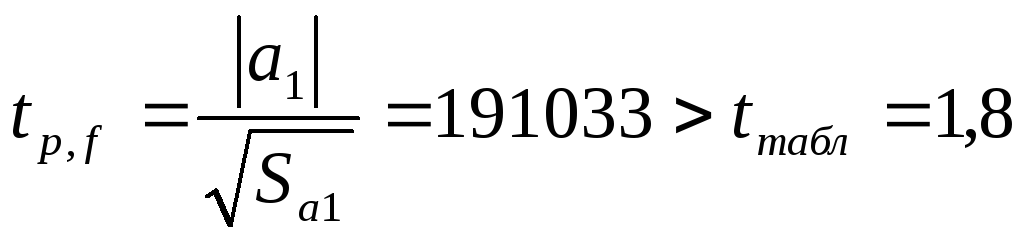– коэффициент значимый

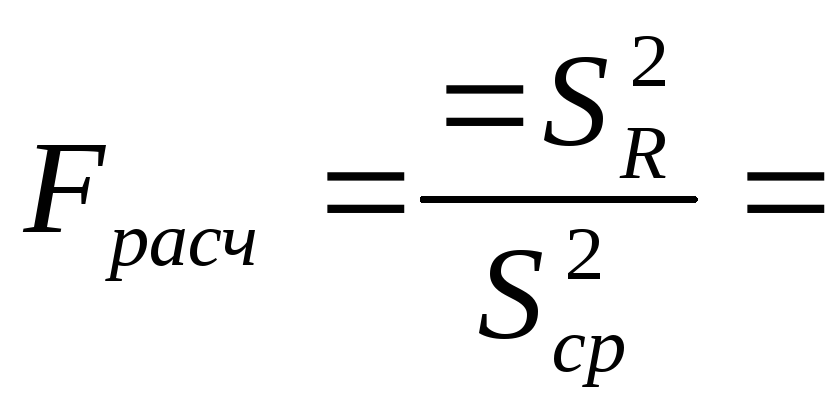1,22 – зависимость адекватна.

Исходная зависимость принимает вид:

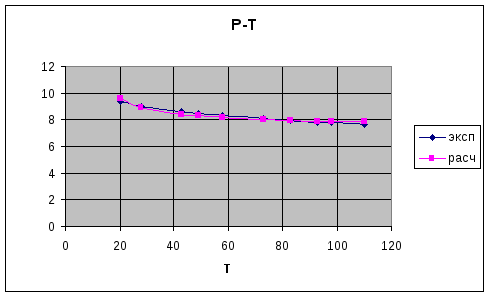
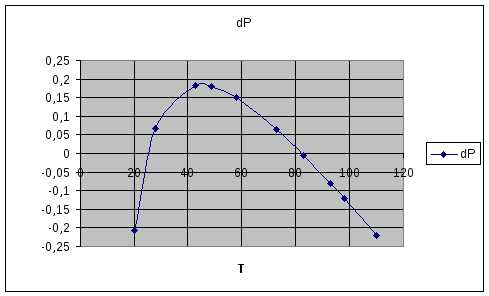
Зависимость номер 2

После логарифмирования данная зависимость принимает вид:

Если и , тогда уравнение примет вид:

Составим систему уравнений:

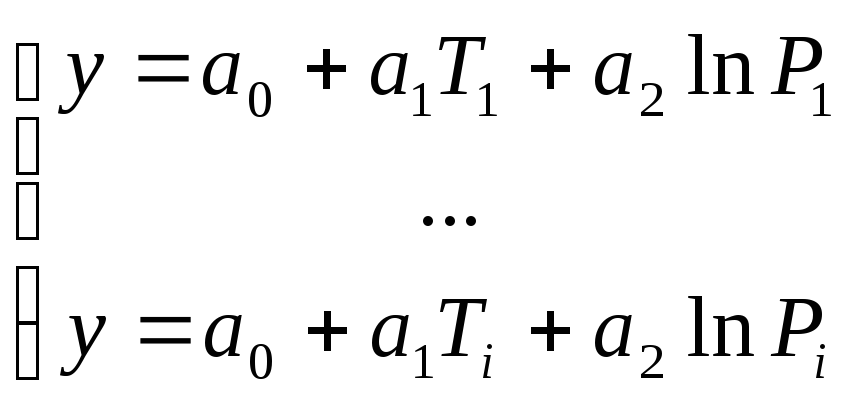
В матричной форме:

, если , тогда

Где матрицы принимают вид:

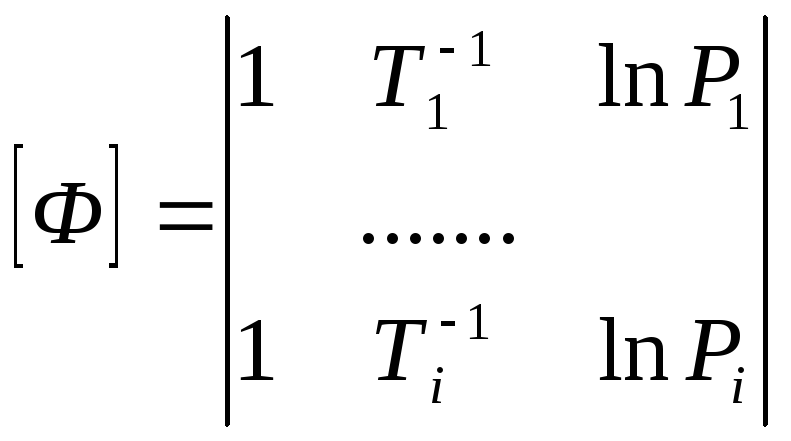
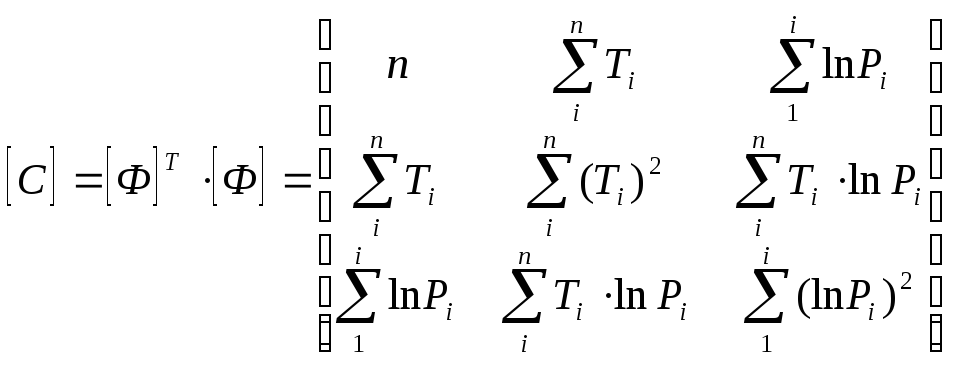
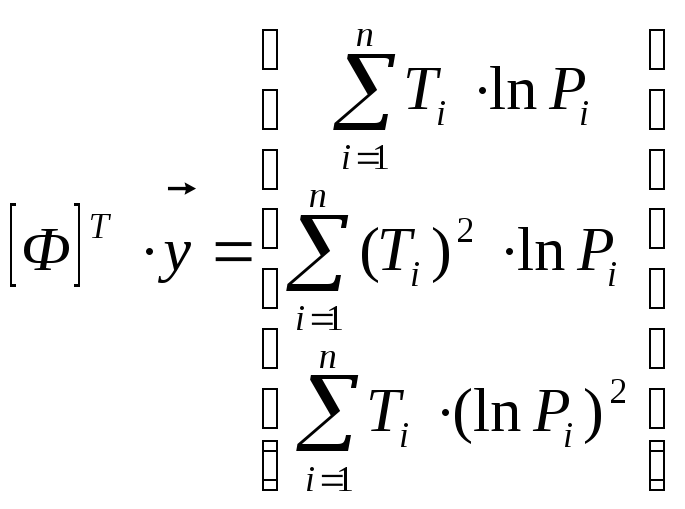
В результате решения системы получены следующие значения коэффициентов регрессии:

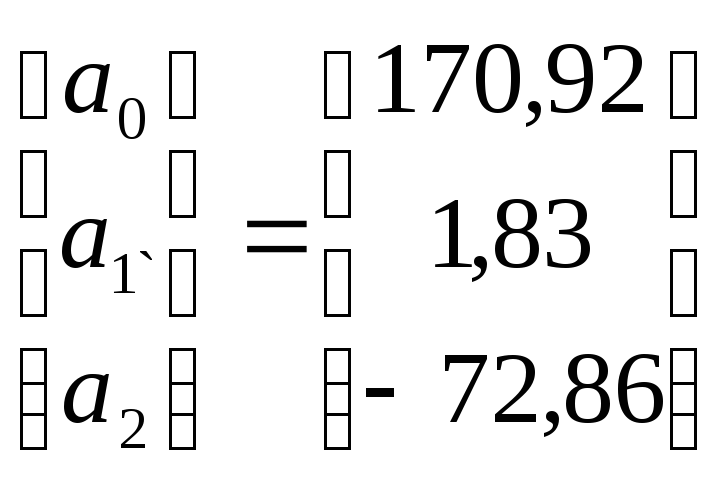
Проверим значимость коэффициентов уравнения регрессии и адекватности уравнения по критерию Фишера

3712,584

– коэффициент не значимый

– коэффициент не значимый

– коэффициент не значимый

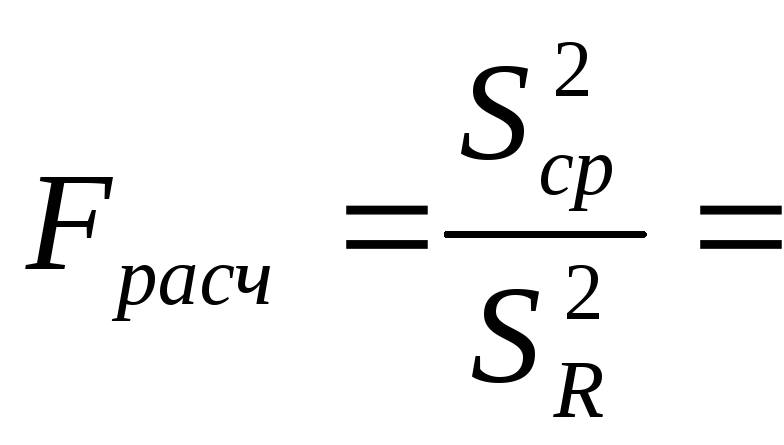16603,685 – зависимость не адекватна

Исходная зависимость принимает вид:

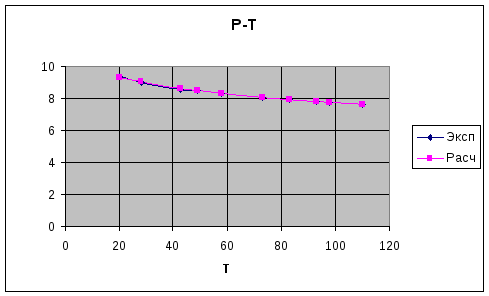
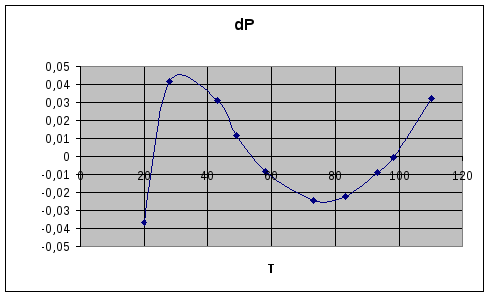
Зависимость номер 3

После логарифмирования данная зависимость принимает вид:

Если и , тогда уравнение примет вид:

Составим систему уравнений:

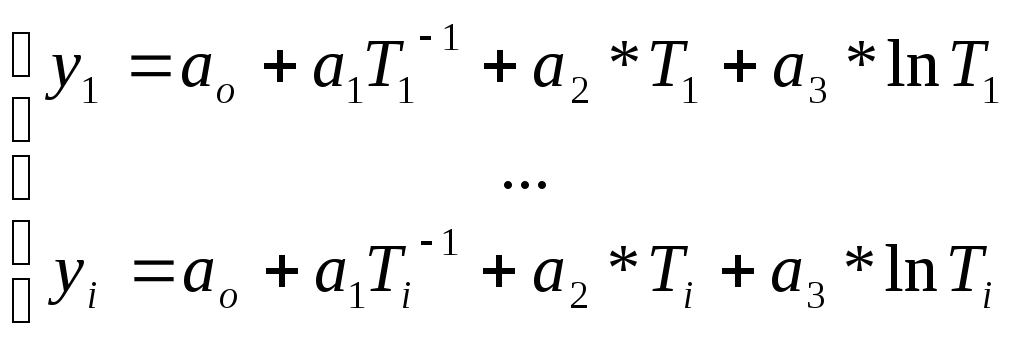
В матричной форме:

, если , тогда

Где матрицы принимают вид:

В результате решения системы получены следующие значения коэффициентов регрессии:

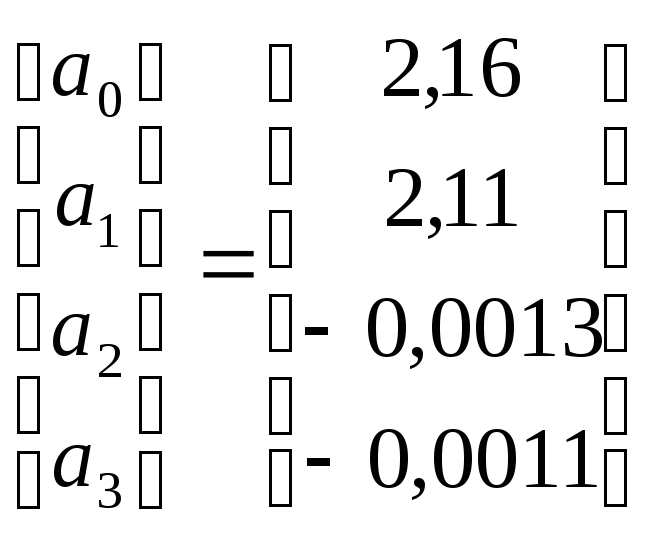
Проверим значимость коэффициентов уравнения регрессии и адекватности уравнения по критерию Фишера

0,0045

– коэффициент значимый

– коэффициент значимый

– коэффициент не значимый

– коэффициент не значимый

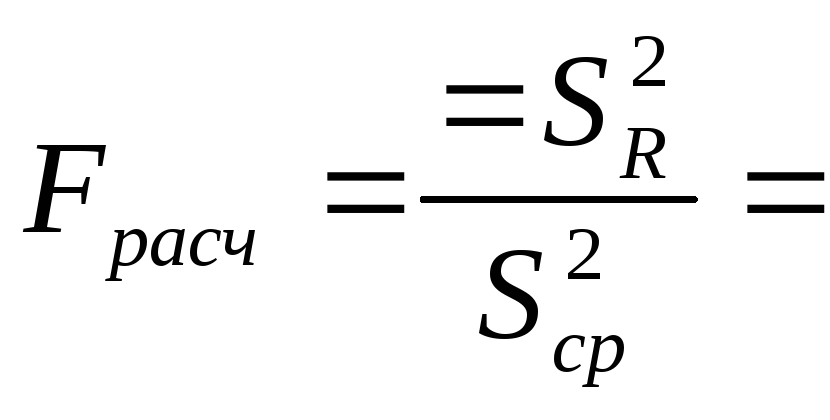100000 – зависимость не адекватна

Исходная зависимость принимает вид:

Зависимость номер 4

После логарифмирования данная зависимость принимает вид:

Если и , тогда уравнение примет вид:

Составим систему уравнений:

В матричной форме:

, если , тогда

Где матрицы принимают вид:

В результате решения системы получены следующие значения коэффициентов регрессии:

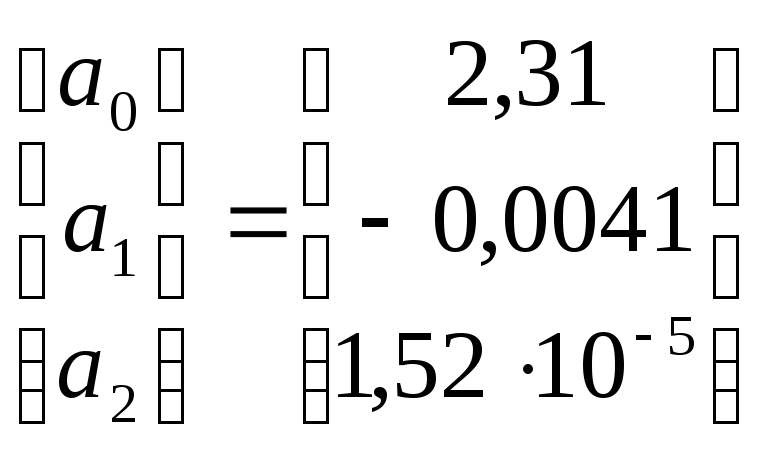
Проверим значимость коэффициентов уравнения регрессии и адекватности уравнения по критерию Фишера

0,0045

– коэффициент значимый

– коэффициент не значимый

– коэффициент не значимый

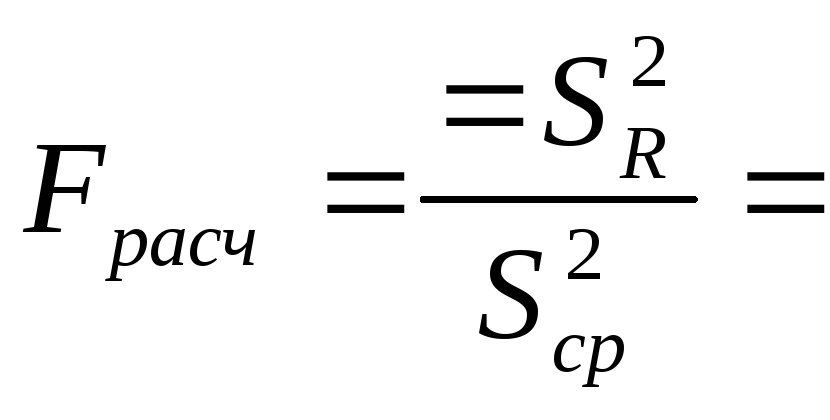131,19 – зависимость не адекватна

Исходная зависимость принимает вид:

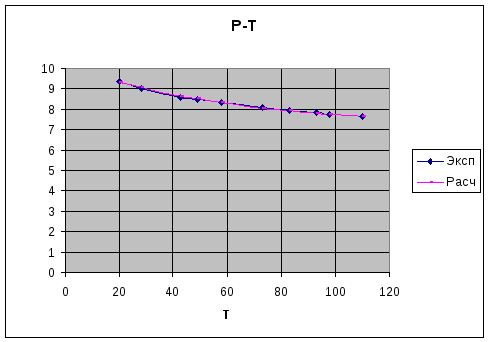
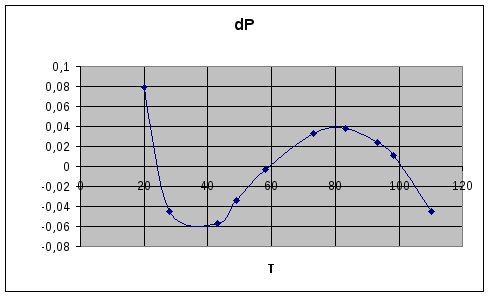
Зависимость номер 5

После логарифмирования данная зависимость принимает вид:

Если и , тогда уравнение примет вид:

Составим систему уравнений:

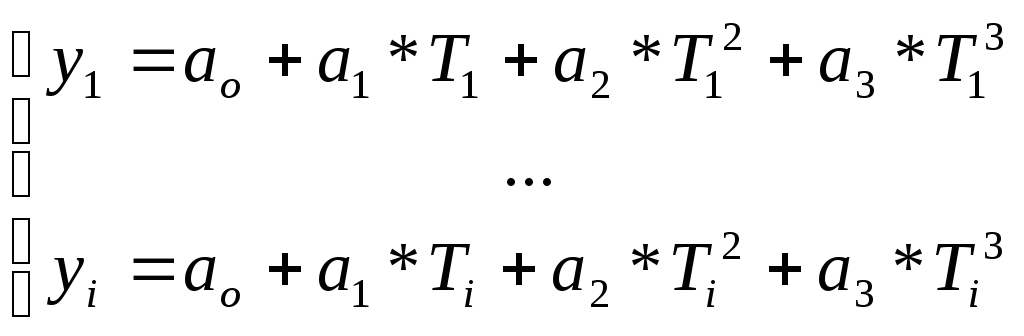
В матричной форме:

, если , тогда

Где матрицы принимают вид:

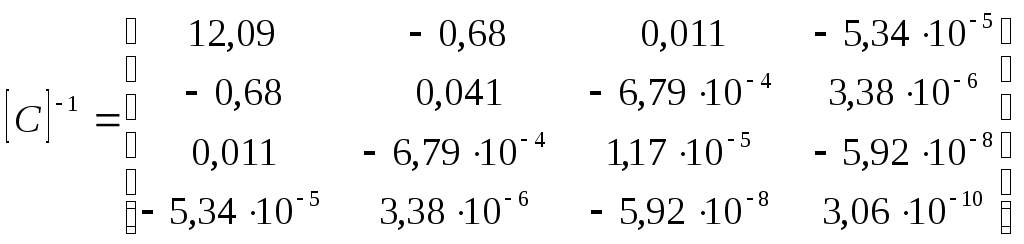
В результате решения системы получены следующие значения коэффициентов регрессии:

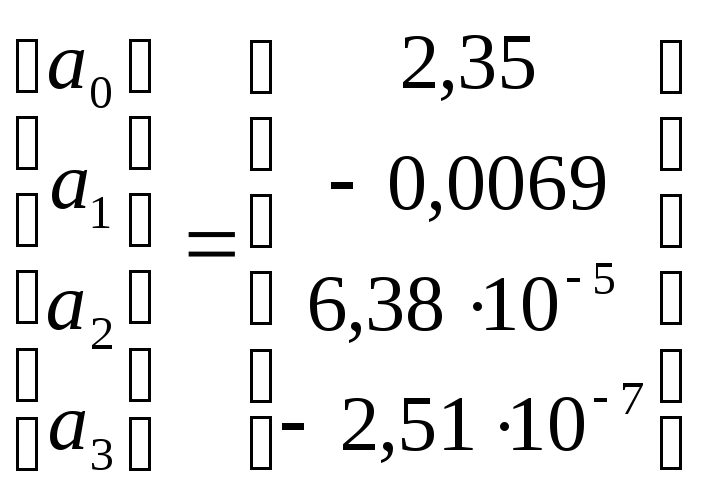
Проверим значимость коэффициентов уравнения регрессии и адекватности уравнения по критерию Фишера

0,0045

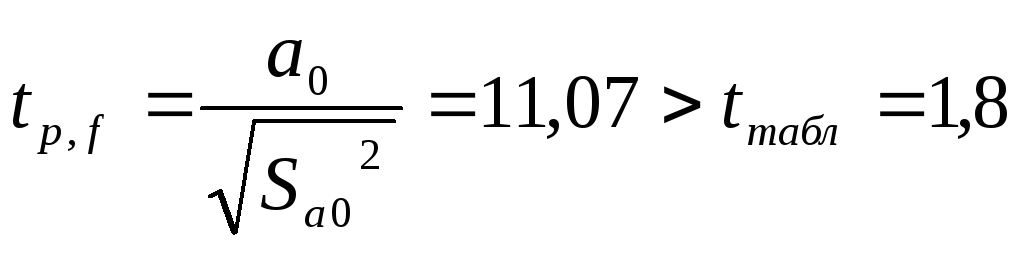– коэффициент значимый

– коэффициент не значимый

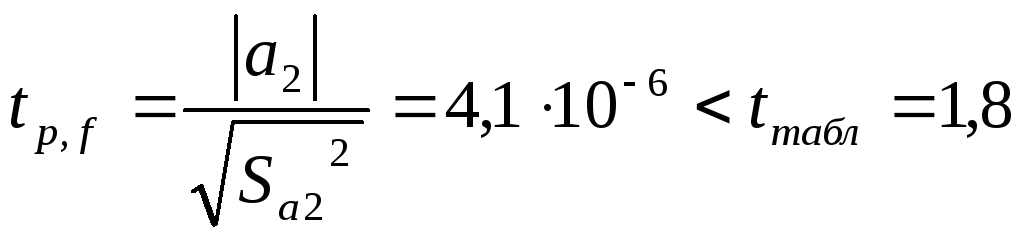– коэффициент не значимый

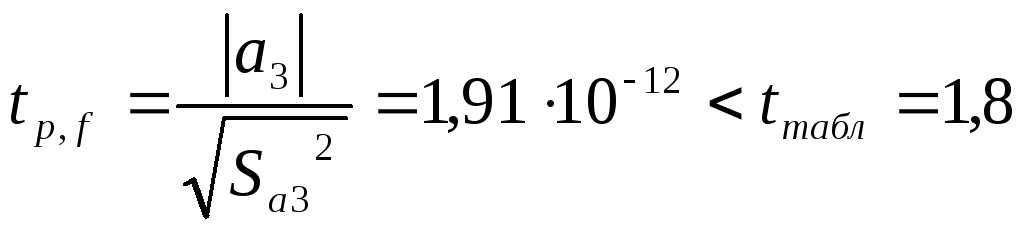– коэффициент не значимый

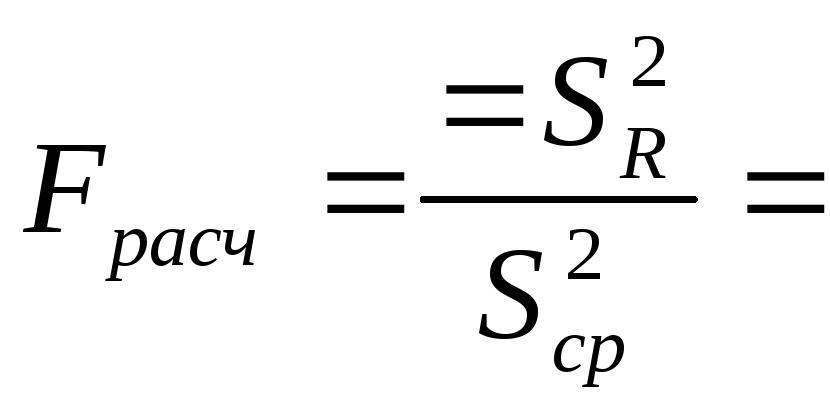767,91 – зависимость не адекватна

Исходная зависимость принимает вид:

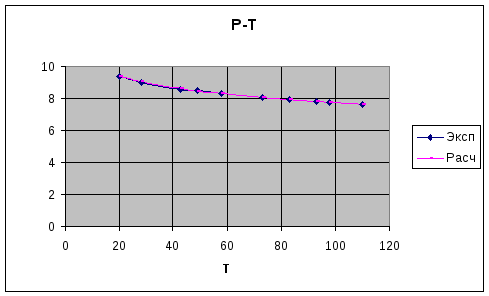
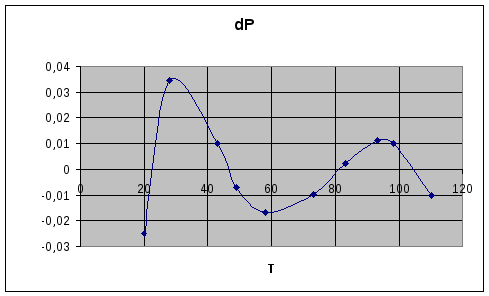
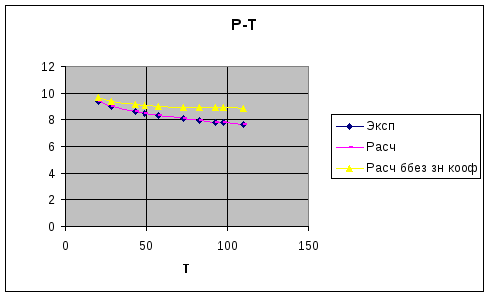
Выводы.

Была произведена обработка данных пассивного эксперимента по определению зависимости давления от температуры. Обработка производилась следующим образом:

1. Определялись коэффициенты уравнений регрессии указанных пяти моделей.

2. Определялась значимость коэффициентов уравнения регрессии используя расчетный и табличный критерии Стьюдента.

3. Определялась адекватность уравнения регрессии с использованием F-распределения Фишера из условия

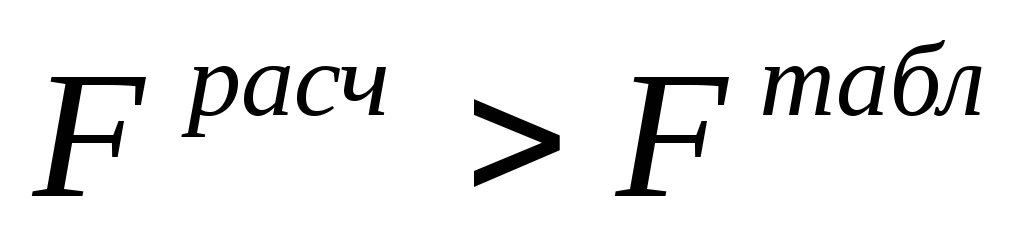
4. Линеаризованные уравнения преобразованы в исходный вид, построены графики экспериментальных и расчетных зависимостей, а также ошибок для каждого уравнения.

Метод наименьших квадратов.

Для нахождения коэффициентов уравнения регрессии в МНК используется критерий наименьших квадратов - min

Минимум критерия соответствует следующей системе уравнений:

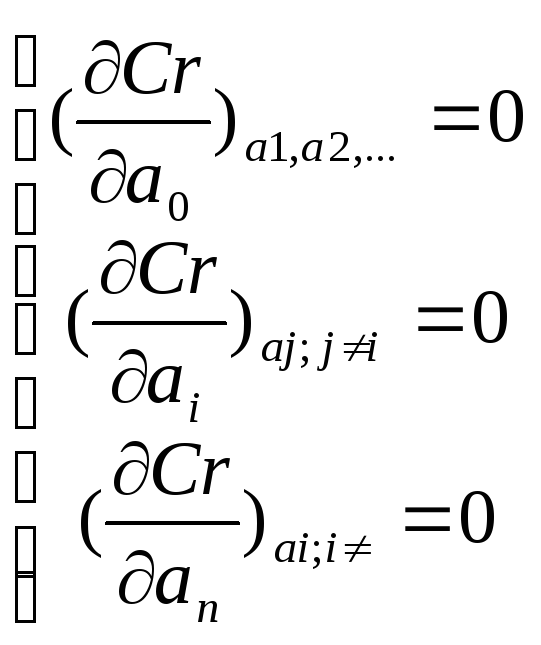
Для зависимости вида

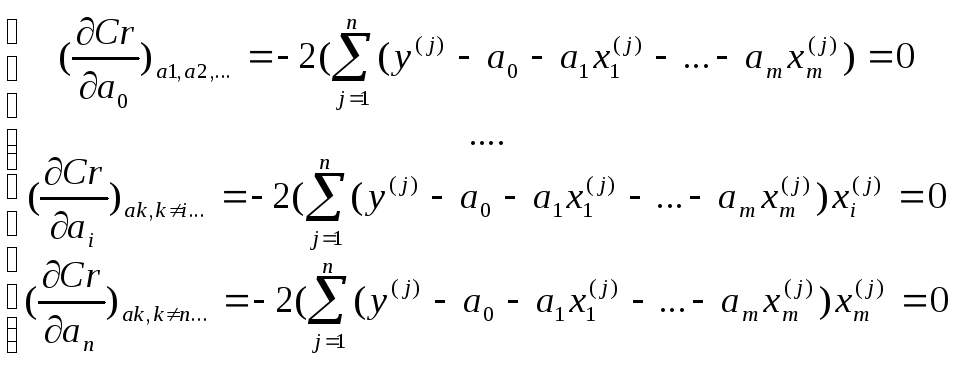
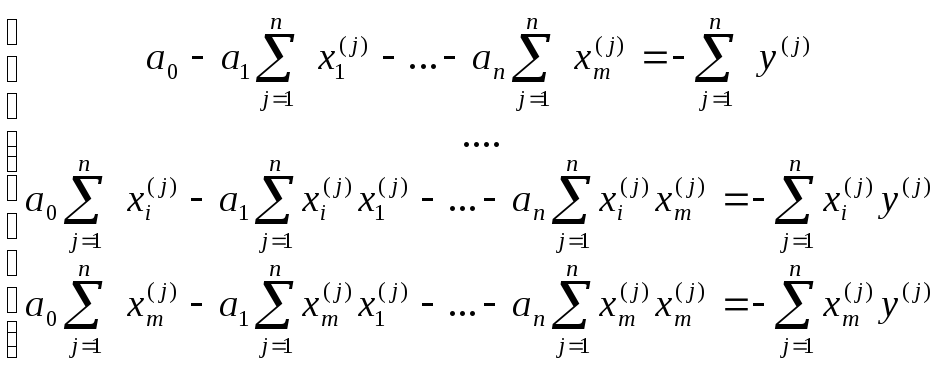
Решая данную СЛАУ получают искомые коэффициенты уравнения регрессии.