Метод Гаусса

Метод Гаусса – алгоритм нахождения решения невырожденных систем линейных уравнений (система линейных уравнений невырожденная, когда её определитель не равен нулю). Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся:

• умножение любого из уравнений на ненулевую константу;

• перестановка уравнений;

• прибавление к уравнению любого другого уравнения системы.

Рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

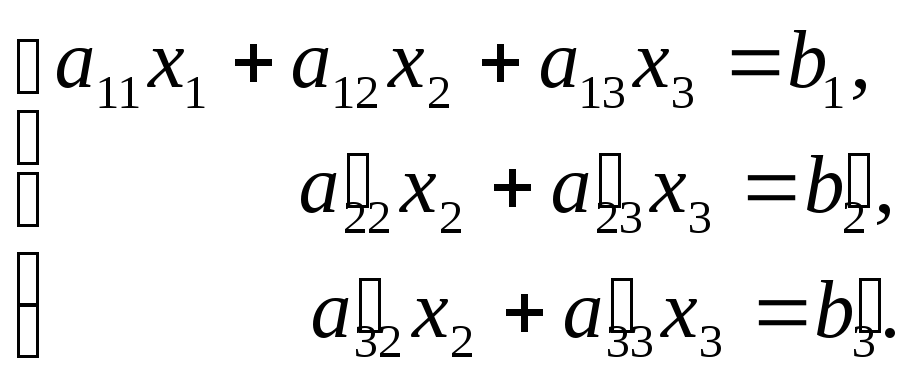
Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим наи сложим со вторым. Тогда будем иметь систему уравнений:

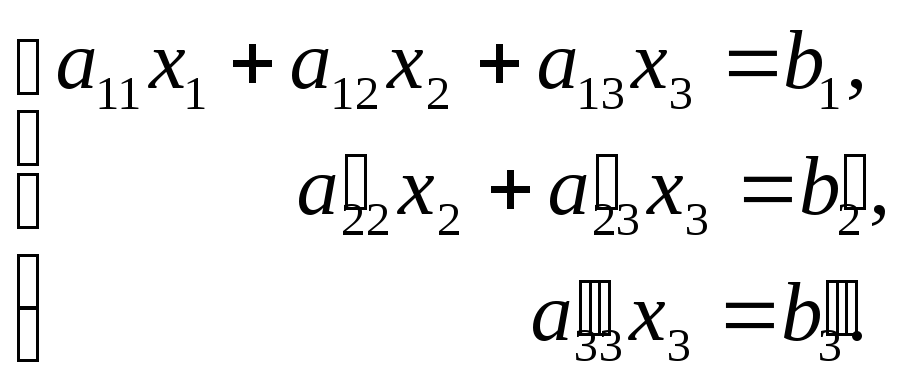
Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

з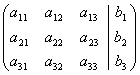атем приводят её к треугольному виду с помощью элементарных преобразований (перестановка строк или столбцов; умножение строки на число, отличное от нуля; прибавление к одной строке другие строки).

Пример. Решить систему уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

2 Векторная алгебра. Координаты и векторы в пространстве

Направленный отрезок с началом в точке и концом в точке называется вектором. Обозначается или строчной буквой латинского алфавита: . Тогда координаты вектора=

Длина отрезка называетсядлиной или модулем вектора и обозначается: , и вычисляется по формуле.

Скалярным произведением векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:

Скалярное произведение в координатах. Пусть векторы ,Тогда скалярно произведениекосинус угла между векторамиможно вычислить по формуле.

Векторным произведением векторовназывается вектор, обозначаемый, и удовлетворяющий трём условиям:

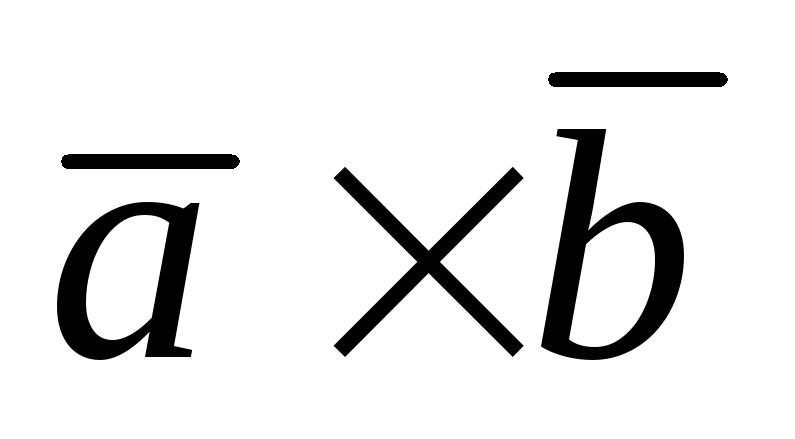• перпендикулярен каждому из перемножаемых векторов,

• его длина ,

• тройка векторов 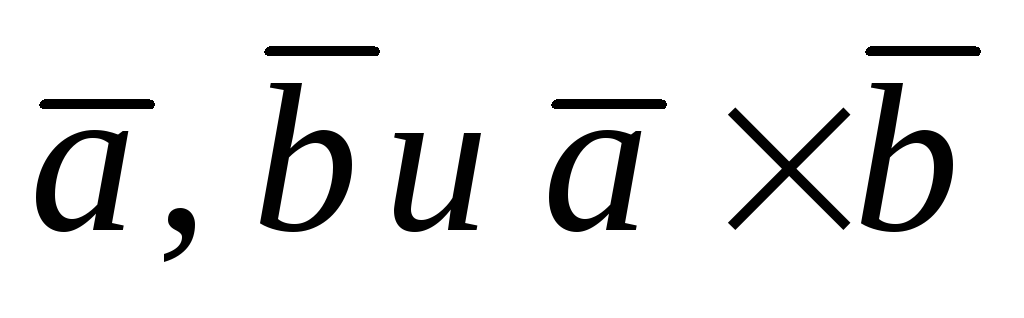- правая.

Векторное произведение в координатах: 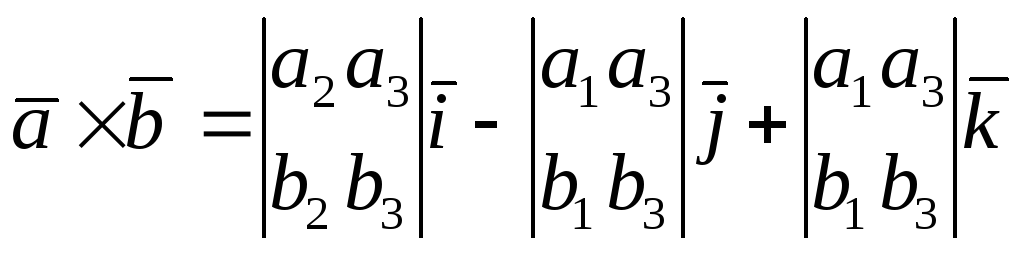. Где-единичные векторы.

Геометрический смысл векторного произведения. Модуль векторного произведения равен площади параллелограмма, построенного на приведенных к общему началу векторах(рисунок 1).

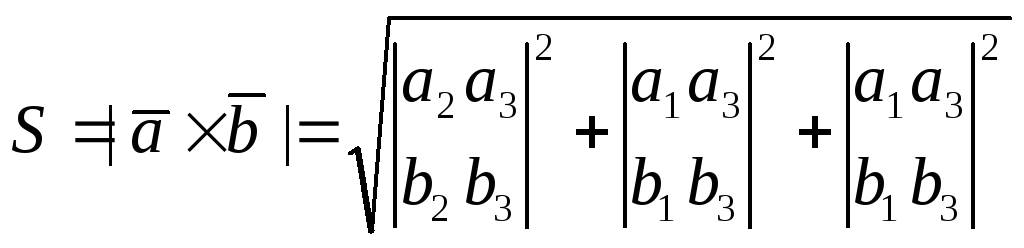
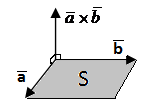
Рисунок 1 - Площадь параллелограмма равна векторному произведению

Смешанным произведением векторов называют векторно-скалярное произведение трех векторов .

Смешанное произведение в координатах., тогда

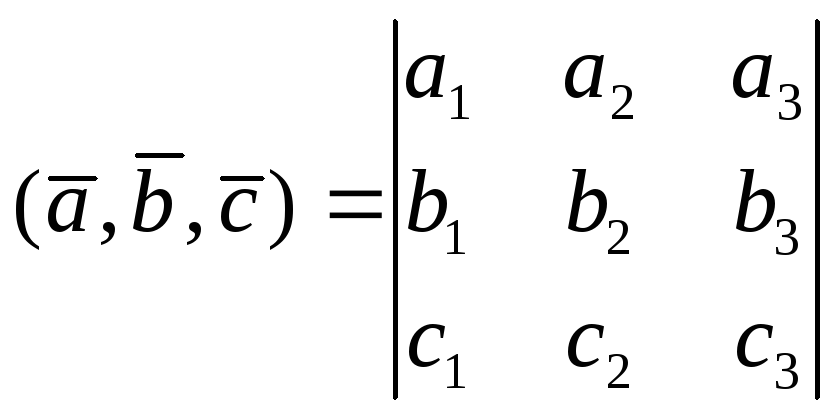
Геометрический смысл . Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку, т.е.