Текст лекции

Введение в лекцию:

В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.

Учебные вопросы лекции:

1. Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков

Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: т, Ϭ для нормального закона, а для закона Пуассона и другие.

Пусть - выборка наблюдений случайной величины X, а θ - неизвестный параметр.

Точечной оценкой неизвестного параметраθ называется приближённое значение этого параметра, полученное по выборке.

Очевидно, что зависит от элементов выборки . Будем считать, что- случайная величина и является функциейсистемы случайных величин, одной из реализации которой является данная выборка.

Точечная оценка должна удовлетворять свойствам:

1. Состоятельность. Оценка 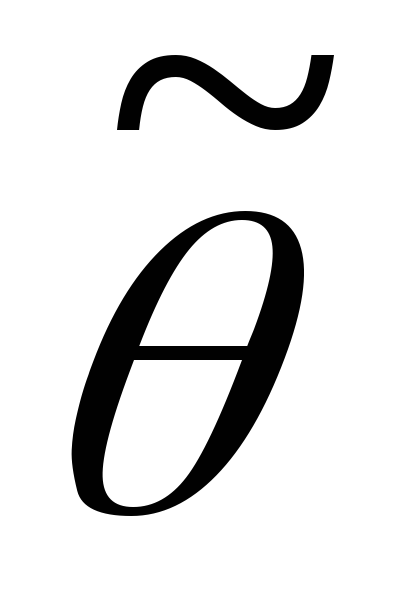параметраθ называется состоятельной, если при.

Состоятельность оценки можно установить с помощью теоремы: если

при , то- состоятельная оценка.

2. Несмещённость. Оценка 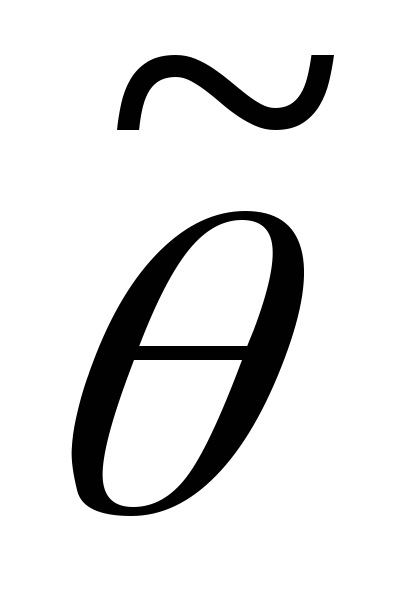параметраθ называется несмещённой,

если . Для несмещённых оценок систематическая ошибка оценивания равна нулю.

Для оценки параметра может быть предложено несколько несмещённых оценок. Мерой точностисчитают её дисперсию. Отсюда вытекает третье свойство.

3. Эффективность. Несмещённая оценка 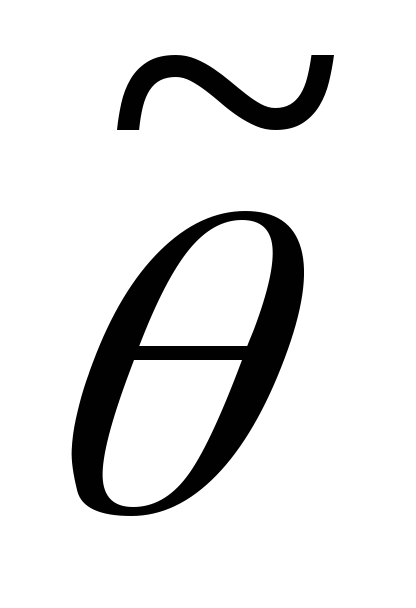параметраθ называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещёнными оценками этого параметра.

Запишем точечные оценки числовых характеристик случайной вели­чины X.

1. Точечная оценка математического ожидания (выборочного среднего)находится по формуле

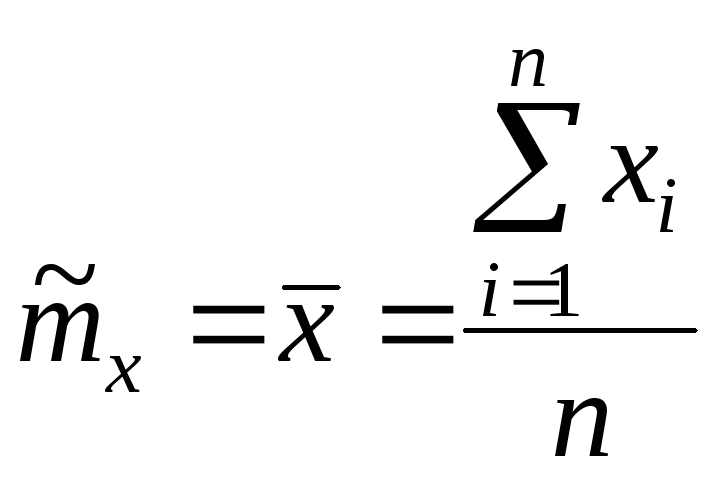. (1)

Проверим свойства оценки:

а) состоятельность следует из теоремы Чебышева: при;

б) несмещённость:

;

в) эффективность:

,

так как при.

2. Точечная оценка дисперсиинаходится по формуле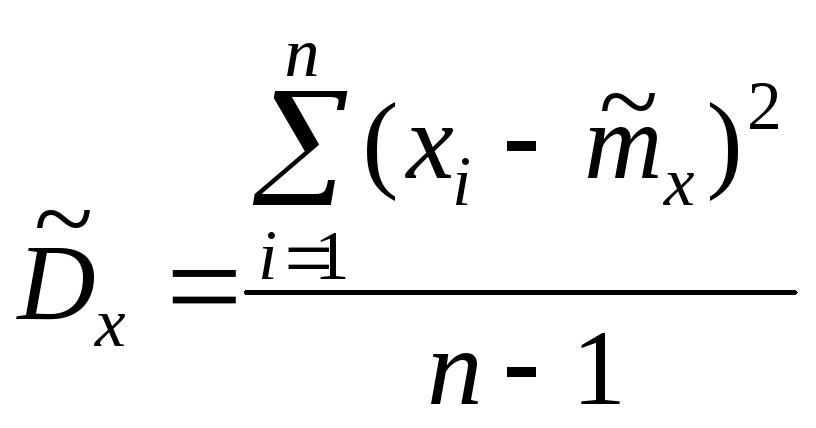, (2)

она обладает свойствами: состоятельность, несмещённость, эффективность.

3. Точечная оценка среднеквадратического отклонения равна

. (3)

1.2. Интервальные оценки.

При статистической обработке результатов наблюдений необходимо знать не только точечную оценку параметраθ, но и уметь оценить точность этой оценки. Для этого введём понятие доверительного интервала, который мы рассмотрим на лекции № 17.

Заключение по лекции:

В лекции мы рассмотрели интервальные оценки параметров распределения генеральной и выборочной совокупности. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Приложения