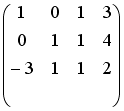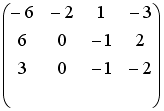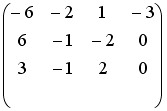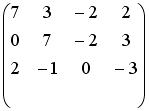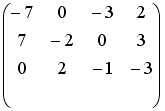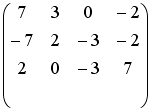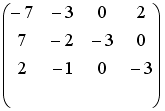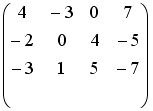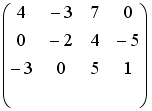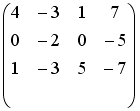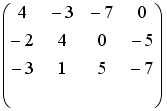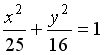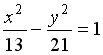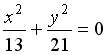- •036401.65 «Таможенное дело»
- •Установите соответствие между матрицей и ее определителем.
- •Установите соответствие между матрицей и ее определителем.
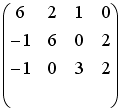
- •Установите соответствие между матрицей и ее определителем.
- •Установите соответствие между матрицей и ее определителем.
- •Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
- •Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
- •Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
- •Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
- •Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
- •Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
- •Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
- •Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
- •Укажите соответствие между уравнениями и видами кривых второго порядка.
- •Укажите соответствие между уравнениями и видами кривых второго порядка.
- •Укажите соответствие между уравнениями и видами кривых второго порядка.
- •Укажите соответствие между уравнениями и видами кривых второго порядка.
- •Укажите соответствие между кривыми второго порядка и их уравнениями:
- •Укажите соответствие между кривыми второго порядка и их уравнениями:
- •Укажите соответствие между кривыми второго порядка и их уравнениями:
- •Укажите соответствие между кривыми второго порядка и их уравнениями:
- •Укажите соответствие между кривыми второго порядка и их уравнениями:
- •Множества
- •Установить соответствия между списками двух множеств, заданных различным образом:
- •Установить соответствия между списками двух множеств, заданных различным образом:
- •Установить соответствия между списками двух множеств, заданных различным образом:
- •Установите соответствие между заданными числами и множествами, которым они принадлежат.
- •Установите соответствие между заданными числами и множествами, которым они принадлежат.
- •Установите соответствие между числовой последовательностью и формулой ее общего члена
- •Установите соответствие между числовой последовательностью и формулой ее общего члена
- •Установите соответствие между числовой последовательностью и формулой ее общего члена
- •Установите соответствие между числовой последовательностью и формулой ее общего члена
-
Даны матрицы
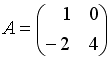 и
и
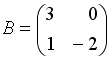 .
Тогда
.
Тогда
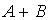 равно
…
равно
…
-
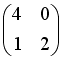
-
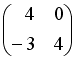
-
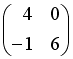
-
+
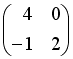
-
-
Даны матрицы
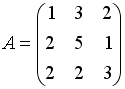 ,
,
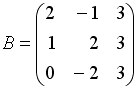 .
Тогда матрица
.
Тогда матрица
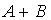 равна…
равна…
-
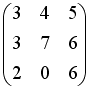
-
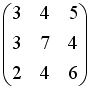
-
+
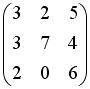
-
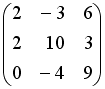
-
-
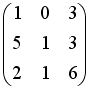
Даны матрицы
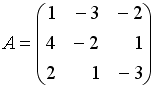 ,
,
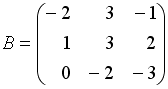 .
Тогда матрица
.
Тогда матрица
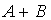 равна
…
равна
…
-
-
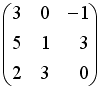
-
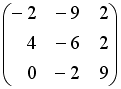
-
+
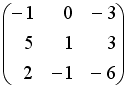
-
-
Даны матрицы
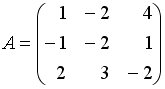 ,
,
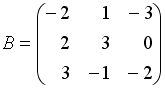 .
Тогда матрица
.
Тогда матрица
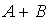 равна
…
равна
…
-
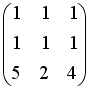
-
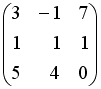
-
+
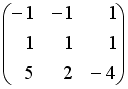
-
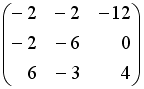
-
-
Если
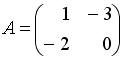 и
и
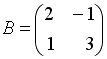 ,
то матрица
,
то матрица
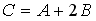 имеет
вид…
имеет
вид…
-
-
+
-
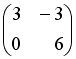
-
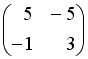
-
-
Умножение матриц
-
Операция произведения матриц правильно определена для матричного умножения вида …
-
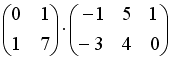 +
+ -
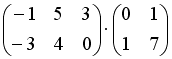
-
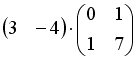 +
+ -
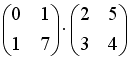 +
+ -
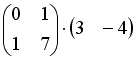
-
-
Операция произведения матриц правильно определена для матричного умножения вида …
-
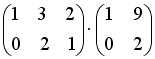
-
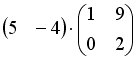 +
+ -
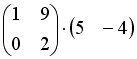
-
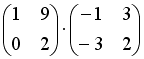 +
+ -
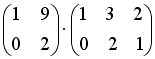 +
+
-
-
Если
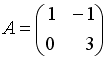 ,
,
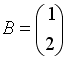 ,
тогда матрица
,
тогда матрица
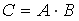 имеет
вид …
имеет
вид …
-
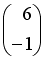
-
+
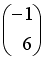
-
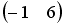
-
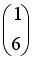
-
-
Даны матрицы
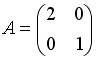 и
и
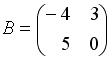 .
Тогда произведение
.
Тогда произведение
 равно
…
равно
…
-
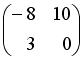
-
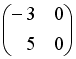
-
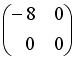
-
+
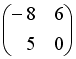
-
-
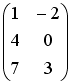
Для матриц А и В найдено произведение
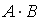 ,
причем
,
причем
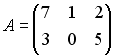 .
Тогда матрицей В может быть матрица …
.
Тогда матрицей В может быть матрица …
-
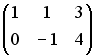
-
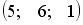
-
+
-
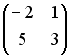
-
-
-
Системы линейных уравнений
-
Дана система уравнений
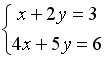 .
Для того, чтобы найти значение переменной
y при решении
этой системы по формулам Крамера,
достаточно вычислить только определители…
.
Для того, чтобы найти значение переменной
y при решении
этой системы по формулам Крамера,
достаточно вычислить только определители…
-
+
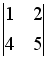 и
и
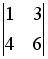
-
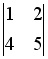 и
и
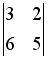
-
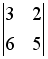 и
и
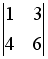
-
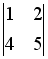 ,
,
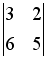 и
и
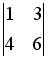
-
-
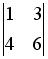
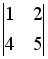
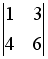
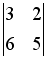
Дана система уравнений
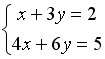 .
Для того, чтобы найти значение переменной
y при решении этой
системы по формулам Крамера, достаточно
вычислить только определители…
.
Для того, чтобы найти значение переменной
y при решении этой
системы по формулам Крамера, достаточно
вычислить только определители…
-
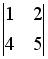 ,
,
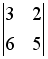 и
и
-
+
 и
и
-
 и
и
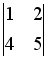
-
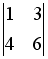 и
и
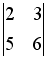
-
-
Система линейных уравнений
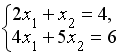 решается
по правилу Крамера. Установите
соответствие между определителями
системы и их значениями.
решается
по правилу Крамера. Установите
соответствие между определителями
системы и их значениями.-
1

-
6
-
2
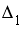
-
14
-
3
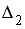
-
- 4
-
2
-
-
Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
-
 1
1
-
23
-
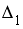 2
2
-
11
-
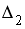 3
3
-
5
-
- 5
-
-
Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
-
 1
1
-
16
-
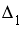 2
2
-
2
-
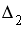 3
3
-
3
-
- 3
-
-
Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
-
 1
1
-
27
-
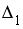 1
1
-
13
-
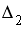 3
3
-
- 3
-
3
-
-
Система линейных уравнений решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
-
 1
1
-
- 1
-
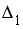 2
2
-
7
-
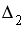 3
3
-
6
-
- 6
-
-
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
-
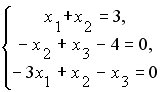 1
1
-
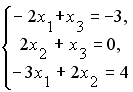 2
2
-
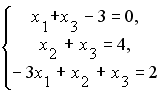 3
3
-
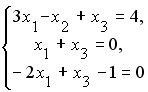 4
4
-
-
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
-
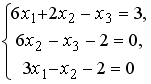 1
1
-
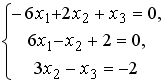 2
2
-
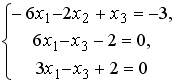 3
3
-
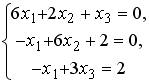 4
4
-
-
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
-
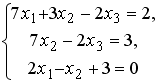 1
1
-
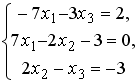 2
2
-
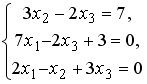 3
3
-
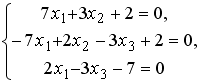 4
4
-
-
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
-
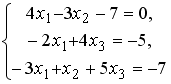 1
1
-
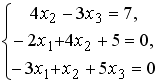 2
2
-
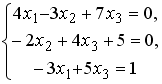 3
3
-
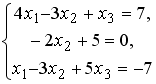 4
4
-
-
-
Основные задачи аналитической геометрии на плоскости
-
Расположите по возрастанию длины сторон треугольника
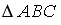 ,
где
,
где
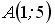 ,
,
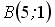 и
и
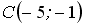 .
.
-
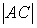
-
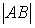 вба
вба -
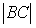
-
-
Расположите по возрастанию длины сторон треугольника
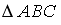 ,
где
,
где
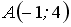 ,
,
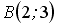 и
и
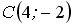 .
.
-
-
 ваб
ваб -
-
-
Расположите по возрастанию длины сторон треугольника
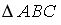 ,
где
,
где
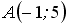 ,
,
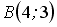 и
и
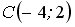 .
.
-
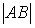
-
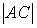 бав
бав -
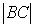
-
-
Расположите по возрастанию длины сторон треугольника
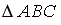 ,
где
,
где
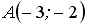 ,
,
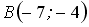 и
и
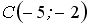 .
.
-
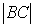
-
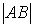 ваб
ваб -
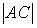
-
-
Расположите по возрастанию длины сторон треугольника
 ,
где
,
где
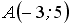 ,
,
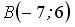 и
и
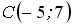 .
.-
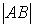
-
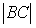 бва
бва
-
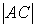
-
-
-
Прямая на плоскости
-
Даны графики прямых:
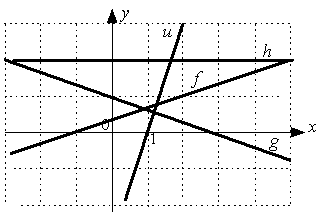 Тогда
сумма их угловых коэффициентов равна…
Тогда
сумма их угловых коэффициентов равна…
-
3
-
-
Даны графики прямых
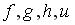 :
:
 Тогда сумма их угловых коэффициентов
равна…
Тогда сумма их угловых коэффициентов
равна…
-
2
-
-
+ Даны графики прямых
 :
:
 Тогда
сумма их угловых коэффициентов равна…
Тогда
сумма их угловых коэффициентов равна…
-
2
-
-
Даны графики прямых
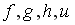 :
:
 Тогда сумма их угловых коэффициентов
равна…
Тогда сумма их угловых коэффициентов
равна…
-
1
-
-
Даны графики прямых
 :
:
 Тогда
сумма их угловых коэффициентов равна…
Тогда
сумма их угловых коэффициентов равна…
-
0
-
-
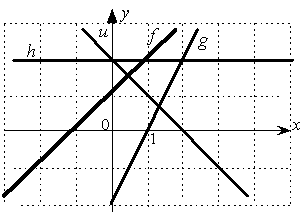
Даны графики прямых
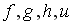 :
:
 Тогда наименьший угловой коэффициент
имеет прямая…
Тогда наименьший угловой коэффициент
имеет прямая…
-
+f
-
h
-
u
-
g
-
-
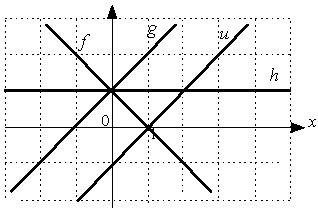
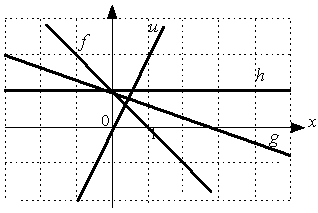
Выберите уравнение прямой, соответствующее данному рисунку.
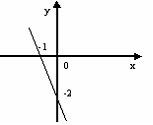
-
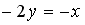
-
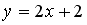
-
+
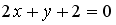
-
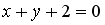
-
-
-
Кривые второго порядка
-
Установите соответствие между кривой второго порядка и ее уравнением.
-
Парабола 1
-
Эллипс2
-
Гипербола 3
-
-
Укажите соответствие между уравнениями и видами кривых второго порядка.
-
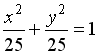 1
1
-
окружность
-
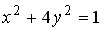 2
2
-
эллипс
-
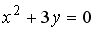 3
3
-
парабола
-
гипербола
-
-
Укажите соответствие между уравнениями и видами кривых второго порядка.
-
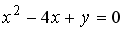 1
1
-
парабола
-
 2
2
-
эллипс
-
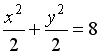 3
3
-
окружность
-
гипербола
-
-
Укажите соответствие между уравнениями и видами кривых второго порядка.
-
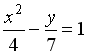 1
1
-
парабола
-
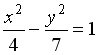 2
2
-
гипербола
-
 3
3
-
эллипс
-
окружность
-
-
Укажите соответствие между уравнениями и видами кривых второго порядка.
-
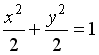 1
1
-
окружность
-
 2
2
-
эллипс
-
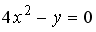 3
3
-
парабола
-
гипербола
-
-
Укажите соответствие между кривыми второго порядка и их уравнениями:
-
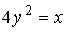 1
1
-
парабола
-
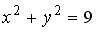 2
2
-
окружность
-
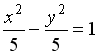 3
3
-
гипербола
-
эллипс
-
-
Укажите соответствие между кривыми второго порядка и их уравнениями:
-
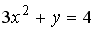 1
1
-
парабола
-
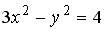 2
2
-
гипербола
-
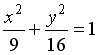 3
3
-
эллипс
-
окружность
-
-
Укажите соответствие между кривыми второго порядка и их уравнениями:
-
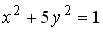 1
1
-
эллипс
-
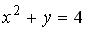 2
2
-
парабола
-
 3
3
-
гипербола
-
окружность
-
-
Укажите соответствие между кривыми второго порядка и их уравнениями:
-
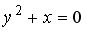 1
1
-
парабола
-
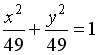 2
2
-
окружность
-
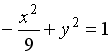 3
3
-
гипербола
-
эллипс
-
-
Укажите соответствие между кривыми второго порядка и их уравнениями:
-
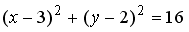 1
1
-
окружность
-
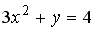 2
2
-
парабола
-
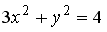 3
3
-
эллипс
-
гипербола
-
-
-
Множества
-
Установить соответствия между списками двух множеств, заданных различным образом:
-
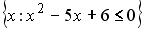 1234
1234
-
-
Установить соответствия между списками двух множеств, заданных различным образом:
-
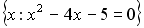 1234
1234
-
-
Установить соответствия между списками двух множеств, заданных различным образом:
-
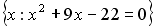 1234
1234
-
-
Установите соответствие между заданными числами и множествами, которым они принадлежат.
-
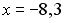 1234
1234
-
-
Установите соответствие между заданными числами и множествами, которым они принадлежат.
-
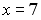 1234
1234
-
-
Мера множества, изображенного на рисунке,
-
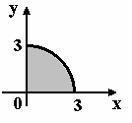
равна…
-
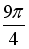 +
+ -
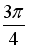
-
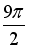
-
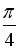
-
Мера множества, изображенного на рисунке,
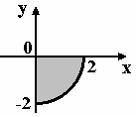
равна…
-

-

-
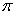 +
+ -
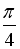
-
Мера множества, изображенного на рисунке,
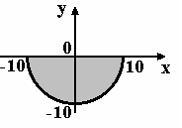
равна…
-
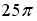
-
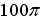
-
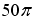 +
+ -
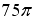
-
Мера множества, изображенного на рисунке,
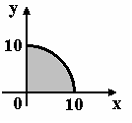
равна…
-
 +
+ -
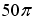
-

-
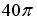
-
Функции: основные понятия и определения
-
Пусть
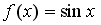 .
Тогда сложная функция
.
Тогда сложная функция
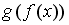 нечетна,
если функция
нечетна,
если функция
 задается
формулами…
задается
формулами…-
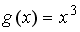 +
+ -
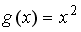
-
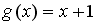
-
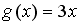 +
+
-
-
Пусть
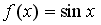 .
Тогда сложная функция
.
Тогда сложная функция
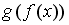 нечетна,
если функция
нечетна,
если функция
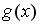 задается
формулами…
задается
формулами…-
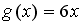 +
+ -
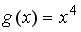
-
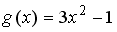
-
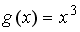 +
+
-
-
Пусть
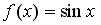 .
Тогда сложная функция
.
Тогда сложная функция
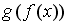 четна,
если функция
четна,
если функция
 задается
формулами…
задается
формулами…-
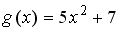 +
+ -
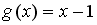
-
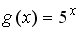
-
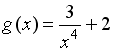 +
+
-
-
Пусть
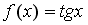 .
Тогда сложная функция
.
Тогда сложная функция
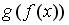 нечетна,
если функция
нечетна,
если функция
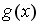 задается
формулами…
задается
формулами…-
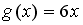 +
+ -
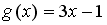
-
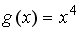
-
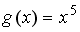 +
+
-
-
Пусть
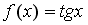 .
Тогда сложная функция
.
Тогда сложная функция
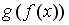 четна,
если функция
четна,
если функция
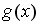 задается
формулами…
задается
формулами…-
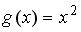 +
+ -
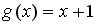
-
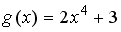 +
+ -
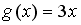
-
-
Областью определения функции
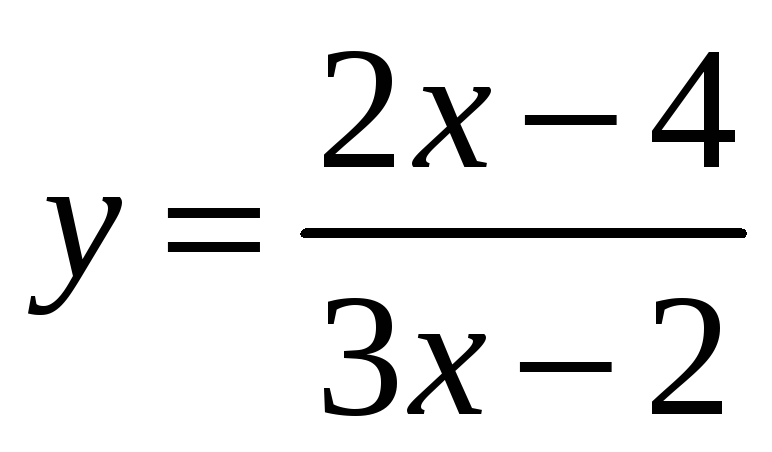 является
множество точек вида
является
множество точек вида
-
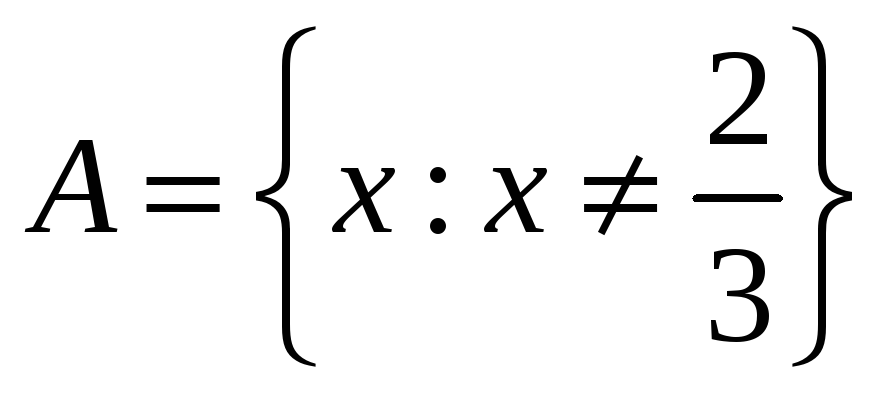 +
+ -
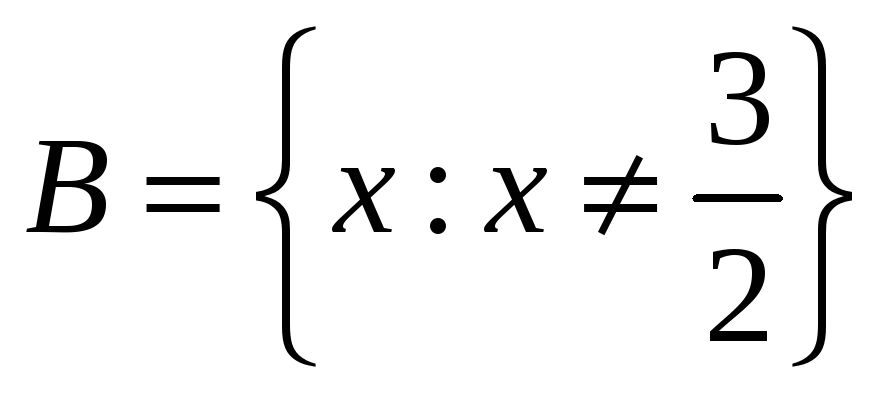
-
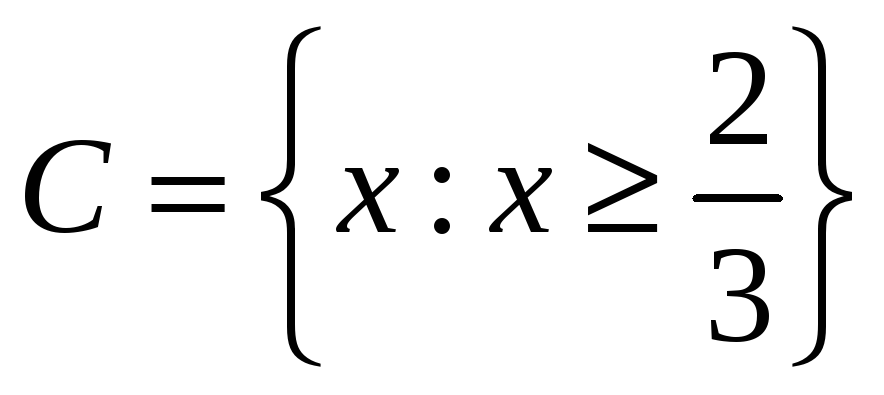
-
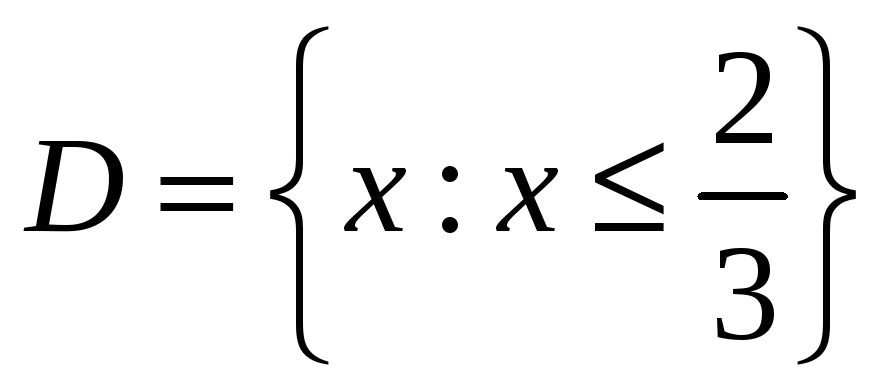
-
-
Областью определения функции
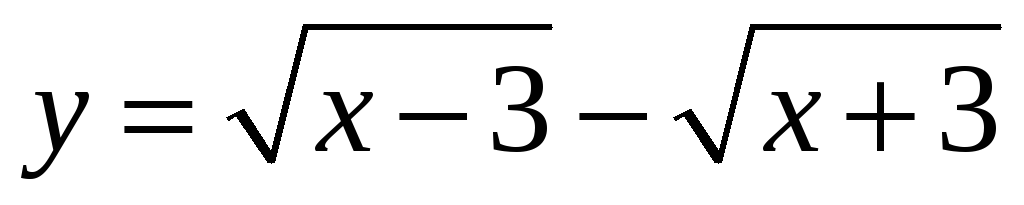 является
множество точек вида
является
множество точек вида
-
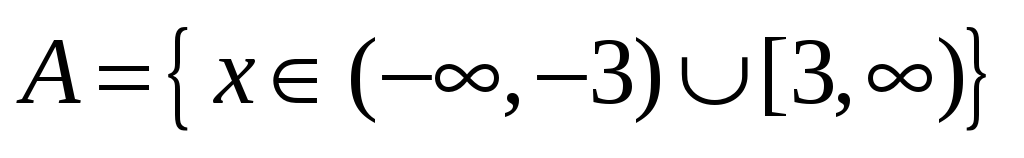
-
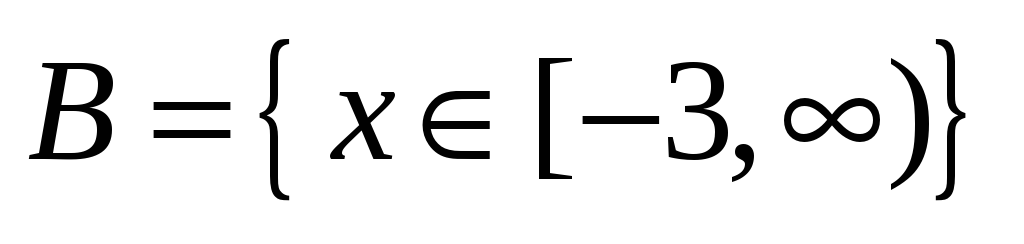
-
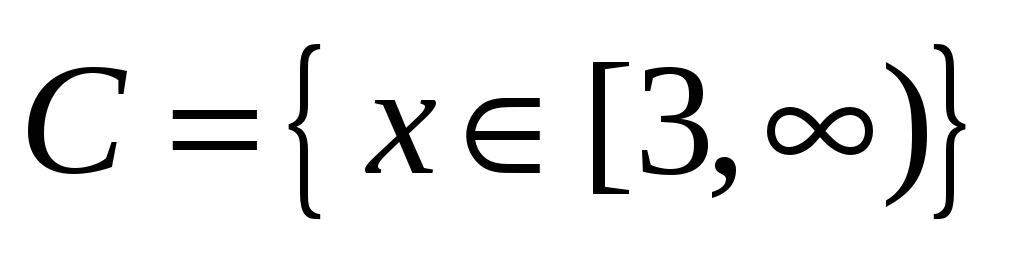 +
+ -
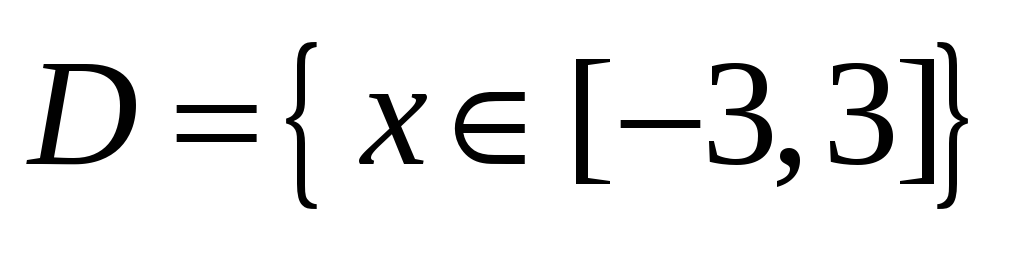
-
-
Областью определения функции
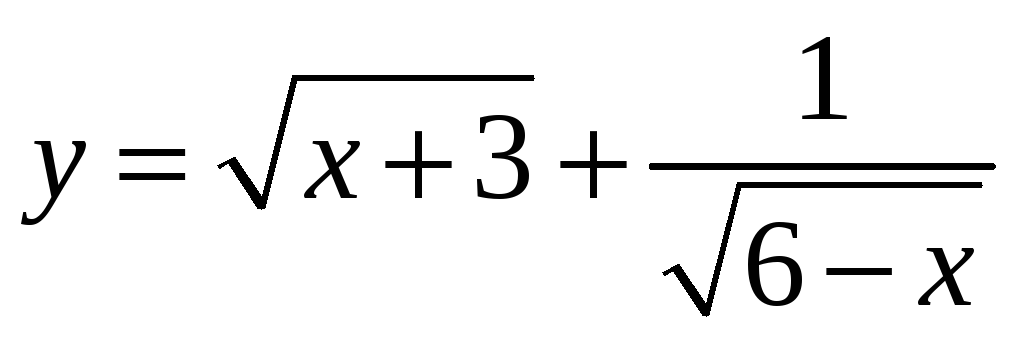 является
множество точек вида
является
множество точек вида
-
-
+![]()