Вопрос №2. Параллельное соединение приемников в однофазных цепях (10 мин.)

Расчет цепи с параллельным соединением проводников (рис. 7,а) можно осуществить различными способами: методом векторных диаграмм, методом проводимостей и методом комплексных чисел. Первый метод не позволяет с большой точностью осуществить расчеты (рис. 7, б), поэтому были введены методы комплексных чисел и метод проводимостей. Рассмотрим метод проводимостей подробнее.

а) б)

Рис. 7. Схема разветвленной цепи и векторная диаграмма

резонанса напряжений

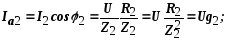
где g₁, g₂ – активные проводимости ветвей;

b₁, b₂ – реактивные проводимости ветвей.

Необходимо отметить, что знак реактивных проводимостей получается автоматически, т.к. ,. Т. к.X_L2 и X_C1 равны нулю, то b₁>0, b₂<0.

Общий ток

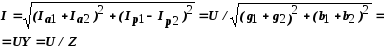где – полная проводимость цепи, См.

Тре­угольник проводимостей представлен на рис. 8.

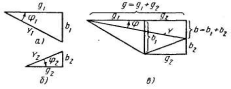
Рис. 8. Треугольники проводимостей

Функции угла φ определяют так:

;

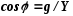
Выражения для мощностей принимают такой вид:

;

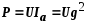Выводы по второму вопросу: таким образом, для расчета цепей с параллельным соединением приемников используются методы векторных диаграмм, проводимостей и комплексных чисел.

Вопрос №3. Резонанс напряжений и токов (20 мин.)

Резонансным режимом работы цепи – режим, при котором ее сопротивление является чисто активным.

Различают два основных режима: резонанс напря­жений и резонанс токов.

3.1. Резонанс напряжений

Резонанс напряжений – это явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.

Рис. 9. Схема последовательного колебательного контура

Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как tgφ=X/R.

Условие резонанса

При резонансе напряжений частота источника равна собственной частоте колебаний контура.

Выражение является формулой Томсона, определяющей зависимость собственной частоты ко­лебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f₀. Вследствие потери колеба­ния в контуре будут затухать, время затуха­ния зависит от значения возникших потерь.

Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 10.

Признаки резонанса напряжений:

а) сопротивление цепи Z=R минимальное и чисто активное;

б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;

в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажи­мах цепи.

Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие по­терь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которой тем больше, чем меньше потери в цепи.

Рис. 10. Векторная диаграмма и резонансная

кривая последовательного контура

Характеристики резонанса:

1) Волновое сопротивление контура

2) Добротность контура

3) Резонансная кривая характеризует способность колебательного контура выделять токи резонансных частот и ослаблять токи других час­тот (рис. 10, б).

4) Полное сопротивление цепи при резонансе

На рис. 11 показана зависимость реактивного сопротивления Х=Х_L -Х_с от частоты источника f. Анализ этого графика показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При час­тотах, близких к f_o, реак­тивное сопротивление мало и ток контура велик.

Рис. 11

Резонанс напряжений широко используется в ра­диотехнике и электронике для выделения сигналов за­данной частоты.