Кристаллографические обозначения атомных плоскостей и направлений

Наличие в одной и той же кристаллической структуре нескольких типов атомных плоскостей и атомных рядов требует специальных приемов их обозначения. В основу обозначения атомных рядов и плоскостей положена их ориентация относительно системы координатных осей XYZ.

В кристаллографии обычно пользуются системами координат, оси которых направлены вдоль ребер элементарной ячейки кристаллической решетки. За единицу измерения вдоль каждой оси принимается период решетки, то есть длина ребер элементарной ячейки.

Кристаллографическими направлениями являются прямые или лучи, выходящие из какой-нибудь точки отсчета, вдоль которых на определенном расстоянии друг от друга располагаются атомы. Точками отсчета могут служить вершины куба, при этом кристаллографическими направлениями, например, являются его ребра, пространственные диагонали или диагонали граней (рис, 5,а).

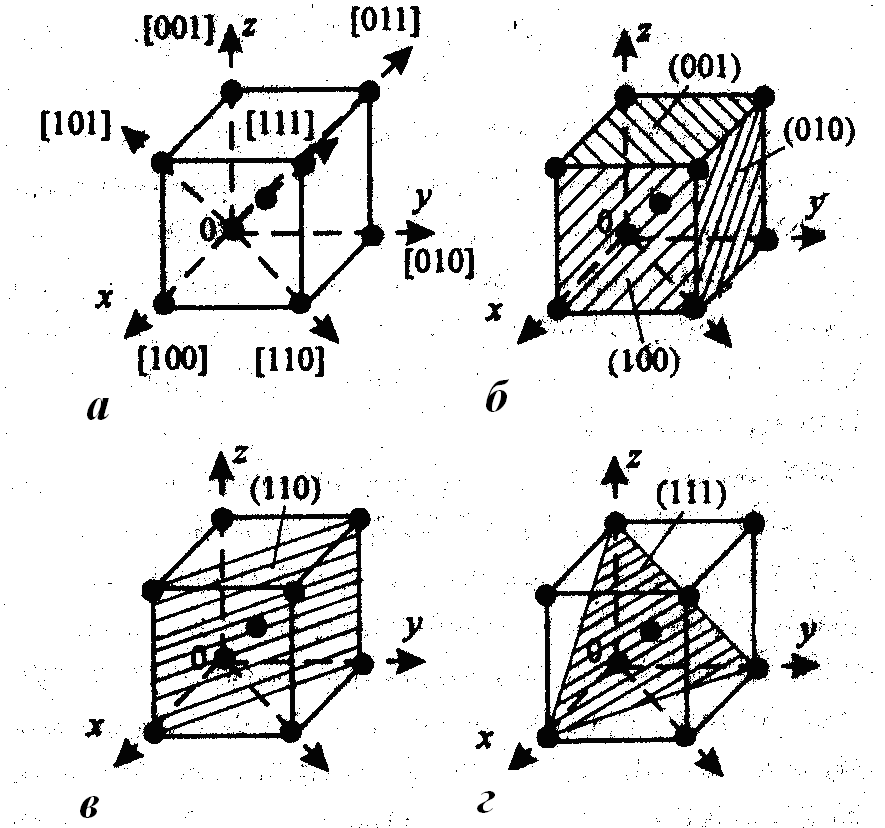
Рис. 5 Основные кристаллографические направления (а)

и плоскости (б, в, г) в ОЦК – решетке

Кристаллографическими плоскостями являются плоскости, в которых лежат атомы, например, грани куба или его диагональные плоскости (рис. 5 б, в, г).

Для обозначения или задания направления (ряда) или плоскости в кристаллах всех сингоний используются так называемые индексы Миллера.

Индексами Миллера для атомного ряда (направления) являются три целых взаимно простых числа u, v, w, соотносящихся следующим образом:

u : v: w = х/а : у/b : z /с

где х, у, z – координаты атома, лежащего на описываемом направлении при условии, что оно проходит через начало координат.

Для того, чтобы определить индексы направления необходимо:

1. задать систему координат таким образом, чтобы направление, индексы которого необходимо определить, проходило через начало координат;

2. следует определить координаты любого атома, лежащего на индексируемом направлении (рис.6).

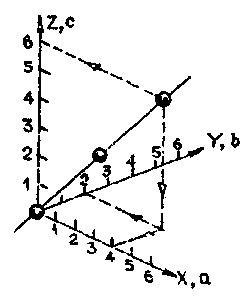
Рис. 6 Схема определения индексов направления

Искомые координаты имеют следующие значения: х = 4а; у = 2b; z = 6с, откуда следует, что

u : v : w = 4: 2: 6, сокращаем и получаем 2 : 1 : 3.

Полученные три взаимно простых числа, заключенные в квадратные скобки и являются индексами данного направления и всех направлений, параллельных ему [2 1 3]. Индексы не разделяются запятыми. Если индекс отрицательный, то знак минус ставится над его значением.

Основные направления в кубической решетке приведены на рис.6 а. Индексы осей решетки 0X – [100], 0Y – [010] и 0Z – [001]. Индексы пространственной диагонали [111].

Индексами Миллера для плоскости являются три наименьших целых безразмерных числа h, k, l, соотносящихся следующим образом:

h : k : l = (1/m)a : (1/ n)b : (1/p)с

где m, n, p – отрезки, отсекаемые искомой плоскостью на осях координат, т.е. индексы кристаллографической плоскости обратно пропорциональны этим отрезкам.

Это определение можно прокомментировать на примере «непрозрачной» плоскости на рис.7. При этом следует обратить внимание, каким графическим приемом обозначена плоскость и ее ориентация относительно системы координат на указанном рисунке. Это осуществляется путем изображения прямых линий – следов пересечения плоскости с координатными плоскостями:

XY. XZ, YZ.

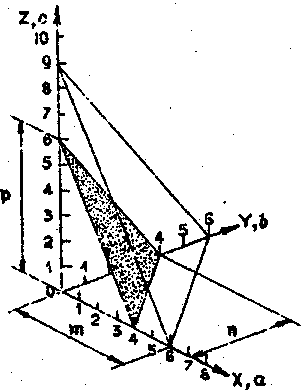
Рис. 7 Определение индексов Миллера для плоскости.

Из рисунка 8 видно, что плоскость отсекает от осей координат следующие отрезки: m = 4a, n = 4b, p = 6c, откуда следует, что

h : k : l = .

Следуя определению, приведенному выше, нельзя отождествлять дробные числа в правой части пропорции с индексами Миллера, так как последние должны быть тройкой наименьших целых чисел. Если каждую дробь умножить на число, являющееся наименьшим общим кратным для знаменателей всех трех дробей, то получатся как раз три наименьших целых числа. В рассматриваемом примере наименьшим общим кратными для знаменателей 4, 4, 6 является число 12. Умножив на него три дроби в правой части пропорции, получим:

h : k : l = 3 : 3 : 2.

Отсюда можно заключить, что индексы Миллера для плоскости h = 3, k =3, l =2.

Индексы Миллера для конкретной плоскости заключаются в круглые скобки и не разделяются запятыми. Если индекс отрицательный, знак минус ставится над ним. Таким образом, «непрозрачная» плоскость на рис. 7 может быть обозначена как (332).

Определим индексы «прозрачной» плоскости на том же рисунке, которая параллельна «непрозрачной». «Прозрачная» плоскость отсекает от осей координат отрезки m = 6a, n = 6b, p = 9c. Отсюда h : k : l = 1/6 : 1/6 : 1/9

Наименьшим общим кратным для знаменателей дробей в правой части полученной пропорции является число 18, поэтому

h : k : l = 3 : 3 : 2.

Следовательно, «прозрачная» плоскость, параллельная «непрозрачной», имеет те же индексы Миллера (332). В более широком смысле этот вывод звучит так: параллельные кристаллические плоскости имеют одинаковые индексы Миллера.

Если плоскость параллельна оси координат, то точка их пересечения находится в бесконечности. Обратное значение отрезка, отсекаемого от оси, равно 1/∞ = 0, т.е. индекс плоскости по этой оси равен 0.

На рис. 5 б, в, г показаны основные атомные плоскости в кубической решетке.