Экономический рост, человеческий капитал и внешние эффекты ю.А. Кузнецов, о.В. Мичасова

Нижегородский государственный университет им. Н.И. Лобачевского

Yu-Kuzn@mm.unn.ru; miov6@yandex.ru

В рамках существующей экономической ситуации одной из наиболее важных задач является обеспечение устойчивого экономического роста, поэтому проблема выявления ключевых факторов и описание механизма их воздействия на экономический рост имеет существенное значение для современной экономической теории.

Одним из таких факторов, несомненно, является человеческий капитал [3,4]. Это понятие в общепринятом теперь виде было введено в 60‑е годы ХХ века Дж. Минцером, Г. Беккером и Т. Шульцем. В настоящее время считается, что человеческий капитал – это совокупность накопленных профессиональных знаний, умений и навыков, получаемых в процессе образования и повышения квалификации, которые впоследствии могут приносить доход – в виде заработной платы, процента или прибыли.

Впервые человеческий капитал (ЧК) был включен в неоклассическую модель экономического роста в классической работе Р. Лукаса [9]. Следует отметить, что первоначально человеческий капитал был своеобразным аналогом научно-технического прогресса. Существенным отличием модели Лукаса от остальных (обзор наиболее известных моделей экономического роста и библиография приведены в [1,5]) является учет как внутреннего (описывающего непосредственное повышение эффективности производства, связанное с ростом квалификации работников), так и внешнего эффекта (характеризующего среднее значение в экономической системе в целом) человеческого капитала. Кроме того, накопление человеческого капитала в модели Лукаса происходит в рамках своеобразного «образовательного сектора экономики», что позволило объяснить различия в темпах экономического роста у разных стран.

Дальнейшее развитие данного направления исследований привело как к детальному изучению, так и к ряду уточнений и обобщений модели Лукаса. Особо отметим работу [8], в которой рассматривается некоторая модификация модели Лукаса, учитывающая «амортизацию» человеческого капитала, наличие убывающей отдачи от масштаба в производственной функции ЧК и присутствие «внешнего эффекта» ЧК не только в сфере производства, но и в сфере образования.

В настоящей работе строится и исследуется математическая модель экономического роста с учетом накопления физического и человеческого капиталов, обобщающая ряд подобных моделей, включая классическую модель Лукаса, и учитывающая как убывающий эффект масштаба в производственной функции ЧК, так и наличие «внешнего эффекта» ЧК в сфере образования. Предполагается также, что экстерналии определяются не только средним уровнем человеческого капитала , но также зависят и от той средней доли времени, которую репрезентативный экономический агент посвящает производственной деятельности . Заметим, что рассматриваемые в работе внешние эффекты человеческого капитала являются характерными для секторов, и не сводятся к среднему уровню ЧК на рынке труда.

, (1)

, (2)

где – функция, описывающая экзогенный технологический прогресс (, ), – доля активного времени, которую репрезентативный экономический агент посвящает производственной деятельности, – численность рабочей силы (, ), – эффективная рабочая сила («внутренний эффект» человеческого капитала), – удельное потребление, – доля физического капитала, – положительный параметр, – норма амортизации физического капитала, – положительный технологический параметр, и – неотрицательные параметры (эластичности), причем , , – норма амортизации.

Оптимизационная задача, связанная с моделью экономического роста с учетом накопления человеческого капитала, состоит в выборе таких управляющих параметров и , которые бы максимизировали величину полной дисконтированной полезности:

, , (3)

на допустимых траекториях , динамической системы (1), (2) при соблюдении условия

, , . (4)

Условие (4) имеет две трактовки, традиционные для неоклассических моделей экономического роста: задача социального планировщика и задача о конкурентном равновесии. Для каждого из этих случаев рассматривались соответствующие оптимизационные задачи, которые после были обобщены. Исследование данной модели подробно изложено в [2]. Основная цель при этом состоит в выявлении и анализе траекторий сбалансированного роста. Их изучение представляет наибольший интерес с экономической точки зрения. Траектория сбалансированного роста (balanced growth path, BGP) – это траектория системы (1)-(3) , для которой темпы роста переменных , и являются постоянным, а – постоянная величина.

Для доказательства существования траекторий сбалансированного роста в обобщенной системе выполняется переход от сопряженных переменных к переменным , где – удельное потребление, а – относительная «теневая цена» человеческого капитала, выраженная в единицах цены физического капитала. Далее осуществляется переход от дифференциального уравнения для относительной теневой цены к дифференциальному уравнению для функции . При этом выполняется также традиционный для неоклассических моделей переход к удельной (на душу населения) величине . Полученная система дифференциальных уравнений позволяет не только установить существование траекторий сбалансированного роста, но и изучить вопросы их устойчивости:

, (5)

, (6)

, (7)

, (8)

причем условия трансверсальности принимают вид:

, , (9)

где , (); при получается задача о конкурентном равновесии, а при – задача социального планировщика

Предложение 1. Система обыкновенных дифференциальных уравнений (5) – (8) обладает первым интегралом

, (10)

где и .

Выражения для темпов роста переменных на траекториях системы могут быть получены в явном виде через параметры системы:

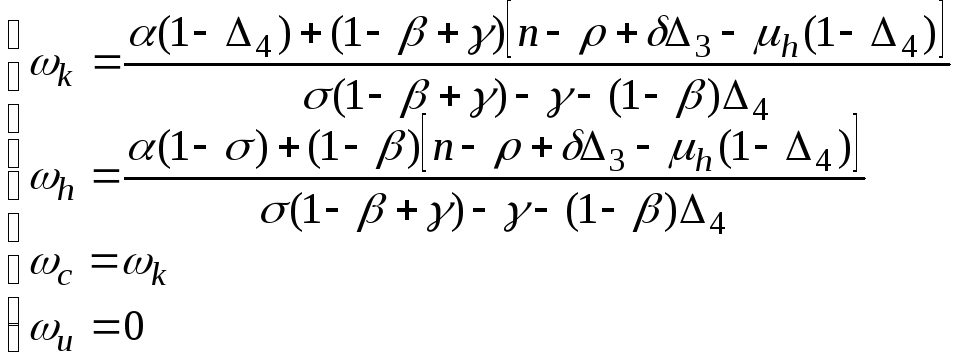(11)

Сопоставление полученных выражений для темпов роста с результатами для модели Лукаса показывает, что темп роста человеческого капитала в предложенной модели ниже, что подтверждается эмпирическими данными.

Для понижения размерности системы (5)-(8) вводятся инструментальные переменные: , . На траекториях сбалансированного роста они являются постоянными. В результате преобразований получается следующая система уравнений:

, (12)

, (13)

, (14)

, (15)

где , , , , ().

Система уравнений (12) – (15) обладает специфической структурой – уравнения (12) – (14) образуют замкнутую подсистему. Поэтому целесообразно исследовать систему трех обыкновенных дифференциальных уравнений (12) – (14). Данная система обладает ненулевым состоянием равновесия. Обозначим его:

, , , (16)

Для изучения системы (12)-(14) в окрестности состояния равновесия (16) стандартным подходом является линеаризация системы в точке и дальнейшее изучение линеаризованной системы:

(17)

где , , а матрица может быть записана через параметры системы стандартным образом [6].

Характеристический полином матрицы имеет вид:

, (18)

где, как известно, (– след матрицы ), , а представляет собой сумму всех главных миноров второго порядка матрицы . Явные выражения коэффициентов через параметры системы имеют достаточно громоздкий вид, поэтому здесь не приводятся. В принципе, явный вид коэффициентов полинома (18) позволяет получить важную информацию о структуре фазового пространства системы (12) – (14) в окрестности состояния равновесия (в зависимости от набора параметров ). Например, в соответствии с классической теоремой Рауса – Гурвица количество корней полинома (18) в правой полуплоскости комплексной плоскости совпадает с числом перемен знаков в наборе , где , , , , , , причем, если определители Гурвица () отличны от нуля (что и предполагается), то полином (18) не имеет чисто мнимых характеристических чисел, так что в левой полуплоскости будет располагаться корней этого полинома.

В работе введены в рассмотрение подмножества , . По определению, параметр , если все определители Гурвица () отличны от нуля, а в правой полуплоскости находится ровно корней характеристического полинома матрицы (так что в левой полуплоскости лежит корней). Ясно, что , .

Положим, далее, (так что, по определению, справедливо равенство ). Если , то среди корней характеристического полинома матрицы имеются чисто мнимые или нулевые корни.

В соответствии с классическими результатами качественной теории дифференциальных уравнений могут представиться следующие возможности [6].

Случай . Все корни находятся в левой полуплоскости плоскости . Состояние равновесия устойчиво. Для любых начальных условий из окрестности имеем , , , . Этот факт не позволяет однозначно определить начальные условия для функций и в задачах (1)-(3), (12)-(15). Другими словами, не представляется возможным выделение единственной траектории, сходящейся к BGP. Следовательно, имеет место ситуация неопределенности (в смысле Дж. Бенхабиба).

Случай . В правой полуплоскости плоскости находится 1 корень. Состояние равновесия неустойчиво и является или седлом, или седло-фокусом. Все траектории, полностью лежащие в двумерном локально устойчивом многообразии приближаются при к состоянию равновесия, а все траектории, лежащие в одномерном неустойчивом многообразии, наоборот, при удаляются от состояния равновесия. Задание начального условия не позволяет однозначно определить начальные условия для функций и . Как и в предыдущем случае, имеет место ситуация неопределенности.

Случай . В правой полуплоскости находится 2 корня. Состояние равновесия системы (12)-(14) неустойчиво и является либо седлом, либо седло-фокусом с одномерным локально устойчивым многообразием и двумерным неустойчивым многообразием. Задание начального условия (в достаточно малой окрестности точки ), вообще говоря, позволяет однозначно определить начальные условия для функций и , а значит, выделить единственную траекторию, сходящуюся к BGP. Следовательно, при реализуется ситуация (локальной) определенности.

Случай . В правой полуплоскости находится 3 корня. Состояние равновесия неустойчиво и является или неустойчивым узлом, или неустойчивым фокусом. Все траектории при удаляются от состояния равновесия и ни одна траектория системы не сходится к BGP. Следовательно, и в этом случае имеет место ситуация неопределенности.

Таким образом, наличие эффекта неопределенности в рассматриваемой модели вытекает из справедливости соотношения: .

В связи с этим заметим следующее. Системы неравенств, задающие как само множество , так и его подмножества (), носят весьма громоздкий характер и не позволяют получить простые аналитические представления для их границ. Поэтому использование таких представлений малоэффективно; гораздо более информативным и наглядным оказывается подход, основанный на использовании возможностей компьютерных систем.

Рассматриваемая модель может использоваться для исследования экономической динамики в первую очередь развитых стран, так как человеческий капитал именно таких стран обладает эффектом убывающей отдачи от масштаба. Поэтому целесообразным представляется изучение динамики системы для набора параметров, равных или близких к реальным значениям для развитых стран (типа Германии или США).

Следует отметить, что проблема определения реальных значений параметров для тех или иных моделей экономического роста остается одной из наиболее актуальных проблем. Большая часть работ в данной области содержит либо исключительно иллюстративные примеры, основанные на интуитивных оценках коэффициентов, либо оценку того или иного вида регрессий, которые позволяют определить степень влияния разного рода факторов на экономический рост, но не дают оценки параметров для моделей типа Лукаса. Однако существует работы, в которых предприняты попытки оценивания коэффициентов для моделей экономического роста с учетом человеческого капитала [8], поэтому их результаты, с учетом ряда замечаний, могут быть использованы для численного моделирования:

Остальные параметры – вектор характеризует экстерналии в производственном секторе и эффект отдачи от масштаба в образовательном секторе. Опишем лишь некоторые результаты качественного анализа динамических особенностей системы (12)-(14) в зависимости от выбора вектора (используемая ниже терминология является общепринятой [6]), полученные с помощью системы компьютерной математики MatLab. Ограничимся случаем конкурентной экономической системы ().

Непосредственный численный анализ корней полинома (18) показывает, что множества , , не пусты и «достаточно представительны» по набору элементов при всех (в том смысле, что эти множества из пространства имеют положительный объем).