По результатам измерения адсорбции на активированном угле рассчитайте удельную поверхность адсорбента (величина адсорбции указана в расчете на азот при нормальных условиях):

P·10-2, Па	А·103, м3/кг
1,85	5,06
4,01	9,90
68,80	40,83

Экзаменационный билет № 5

Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (уравнение Жюрена).

Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:

F – количество степеней свободы, К – количество компонентов, Ф – количество фаз.

Р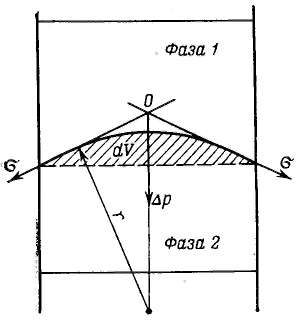ассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.

Кривизна вызывает изменение площади и положения межфазной поверхности, что можно выразить приращением поверхностной энергии σds. Кроме того, изменяются объемы фаз V₁ и V₂ на dV₁ и dV₂. При условии постоянства объема всей системы dV₁ = - dV₂. Изменение объемов вызывает соответствующие изменения энергий фаз 1 и 2 на p₁dV₁ и p₂dV₂ (где p₁ и р₂ — давления внутри фаз). Соотношение между поверхностной энергией и «объемной» можно записать с помощью обобщенного уравнения первого и второго начал термодинамики относительно энергии Гельмгольца F при T=const:

При равновесии между фазами ΔF = 0, тогда

Это уравнение называется уравнением Лапласа.

Для сферической поверхности и уравнение принимает вид.

Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от того, смачивает или не смачивает жидкость стенки сосуда, точнее, от значения краевого угла.

Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотойh:

Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания θ и радиус капилляра r₀. На рисунке показан мениск жидкости в капилляре. Видно, что r₀ = r·соsθ, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:

Нередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие.