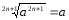9.Корінь н-го степеня. Дії над радикалами
.docxПлан-конспект уроку
з алгебри та початків аналізу
для групи Р-11
Тема уроку: Корінь n-го степеня і його властивості. Дії над радикалами.
Мета уроку: Повторити відомості про квадратний корінь. Формування понять корінь п-го степеня і арифметичний корінь п-го степеня. Вивчення властивостей коренів п-го степеня.
І. Аналіз контрольної роботи №1.
II. Повторення відомостей про квадратний корінь.
Повторити відомості про квадратний корінь можна у вигляді фронтальної бесіди з використанням таблиці 13.
Питання до класу
1. Що називається квадратним коренем з числа?
2. Чому дорівнює квадратний корінь з чисел:
а) 25; б)16; в) 100; г) 0; д) -10?
3. Чому квадратний корінь з від'ємного числа не існує?
4. Що називається арифметичним квадратним коренем з числа а?
III. Сприймання і усвідомлення нового матеріалу.
!Коренем п-го степеня із дійсного числа а називається число, n-й степінь якого дорівнює а.
Наприклад: корінь третього степеня із числа 8 дорівнює 2, бо 23 = 8. Корінь четвертого степеня з числа 81 є числа 3 і -3, бо 34 = 81, (-3)4 = 81.
Згідно даного означення, корінь п-го степеня — це корінь рівняння хn = а. Число коренів цього рівняння залежить від п і а.
Якщо п
– парне,
тобто п =
2k,
k
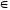 N,
то рівняння х2k
=
а
має два корені, якщо а
> 0; один
корінь, якщо а
= 0;
не має коренів, якщо а
< 0.
N,
то рівняння х2k
=
а
має два корені, якщо а
> 0; один
корінь, якщо а
= 0;
не має коренів, якщо а
< 0.
Якщо п
– непарне,
тобто п =
2k
+ 1,
k
 N,
то рівняння х2k+1
= а завжди
має лише один корінь.
N,
то рівняння х2k+1
= а завжди
має лише один корінь.
!Арифметичним коренем n-го степеня із невід'ємного числа а називається таке невід'ємне число, n-й степінь якого дорівнює а.
Арифметичний
корінь п-го
степеня із числа а
позначають так:
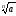 .
Число n
називають показником кореня, число а
– підкореневим
числом (виразом).
.
Число n
називають показником кореня, число а
– підкореневим
числом (виразом).
Якщо п
= 2, то замість
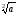 пишуть
пишуть
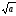 і називають арифметичним квадратним
коренем.
і називають арифметичним квадратним
коренем.
Арифметичний корінь третього степеня називають кубічним коренем.
У тих випадках, коли зрозуміло, що мова йде про арифметичний корінь n-го степеня, коротко говорять «корінь п-го степеня».
Приклад. Знайдемо значення:
а)
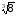 ;
б)
;
б)
 ;
в)
;
в)
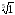 ;
г)
;
г)
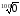 .
.
а)
 = 2, оскільки 23
= 8 і 2 > 0;
= 2, оскільки 23
= 8 і 2 > 0;
б)
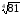 =
3, оскільки 34
= 81 і 3 > 0;
=
3, оскільки 34
= 81 і 3 > 0;
в)
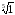 = 1, оскільки 15
= 1 і 1 > 0;
= 1, оскільки 15
= 1 і 1 > 0;
г)
 = 0 , оскільки
0100
= 0.
= 0 , оскільки
0100
= 0.
Приклад. Знайдемо значення:
а)
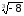 ;
б)
;
б)
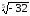 ;
в)
;
в)
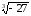 .
.
a)
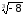 = -
= -
 = -2; б)
= -2; б)
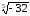 =
-
=
-
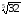 = -2 ; в)
= -2 ; в)
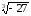 =
-
=
-
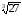 = -3 .
= -3 .
Отже, вираз
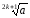 має зміст для будь-якого а
має зміст для будь-якого а
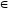 R
і може
набувати будь-яких значень.
R
і може
набувати будь-яких значень.
|
1. Якщо
2.
3.
|
Ми згадали властивості квадратного кореня. Аналогічні властивості мають і корені n-го степеня.
!Властивість
1. Для
невід'ємних чисел а
і b
добуток коренів n-го
степеня із чисел a
і
b
дорівнює кореню n-го
степеня із їх добутку:
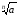 ·
·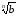 =
=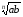 .
.
!Властивість
2. Для
невід'ємного числа а
і додатного числа b
частка
коренів n-го
степеня із чисел а
і b.
дорівнює кореню
n-го
степеня із їх частки:
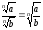 .
.
!Властивість
3. Будь-який
цілий степінь
k
кореня n-го
степеня із невід'ємного числа а
дорівнює кореню n-го
степеня із
степеня k
числа а:
 .
.
!Властивість
4. Щоб
добути корінь із кореня із невід'ємного
числа можна перемножити показники
коренів, а підкореневий вираз залишити
без змін:
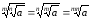 .
.
!Властивість
5. Значення
кореня із степеня невід'ємного числа
не зміниться, якщо показник кореня і
показник підкореневого виразу помножити
(або поділити) на одне і те саме
натуральне
число:
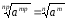 .
.
Виконання вправ
1. Знайдіть значення виразів:
а)
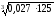 ;
б)
;
б)
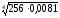 ;
в)
;
в)
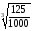 ;
г)
;
г)
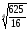 ;
д)
;
д)
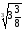 .
.
Відповідь:
а) 1,5; б) 1,2; в) 0,5; г) 2,5; д)
 .
.
2. Обчисліть:
а)
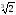 ·
·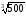 ;
б)
;
б)
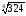 ·
·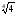 ;
в)
;
в)
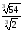 ;
г)
;
г)
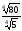 .
.
Відповідь: а) 10; б) 6; в) 3; г) 2.
3. Знайдіть корінь із степеня:
а)
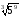 ;
б)
;
б)
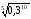 ;
в)
;
в)
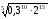 ;
г)
;
г)
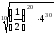 .
.
Відповідь: а) 125; б) 0,09; в) 0,72; г) 16.
4. Спростіть вирази:
а)
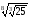 ;
б)
;
б)
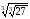 ;
в)
;
в)
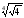 ;
г)
;
г)
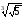 .
.
Відповідь:
а)
 =
=
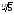 ;
б)
;
б)
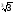 ;
в)
;
в)
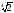 ;
г)
;
г)
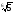 .
.
Вивчені властивості коренів дають змогу виконувати перетворення коренів.
1. Винесення множника з під знака радикала.
В деяких випадках підкореневий вираз розкладається на множники так, що із одного чи декількох із них можна добути точний корінь. Добувши корені із цих множників, одержані числа можна записати перед знаком кореня. Таке перетворення називається винесенням множника за знак радикала.
Наприклад:
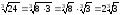 ;
; 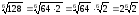 ;
;
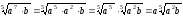 ;
;
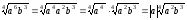 .
.
Взагалі, якщо
a
 0, b
0, b
 0, то
0, то 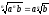 .
.
Якщо
a
– довільне,
то 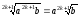 ;
; 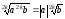 .
.
Виконання вправ
1. Винесіть множники за знак радикала:
а)
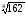 ;
б)
;
б)
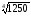 ;
в)
;
в)
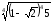 ;
г)
;
г)
 .
.
Відповідь:
а) 3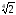 ;
б) 5
;
б) 5 ;
в) (
;
в) (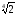 –
1)
–
1)
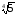 ;
г) (1
–
;
г) (1
–
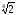 )
)
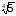 .
.
2. Винесіть множники за знак кореня, якщо а > 0, b > 0:
а)
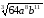 ;
б)
;
б)
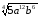 ;
в)
;
в)
 ;
г)
;
г)
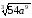 .
.
Відповідь: а)
4a2b3
 ;
б) a3b
;
б) a3b
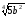 ;
в) –
4a3
;
в) –
4a3
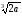 ;
г) 3a3
;
г) 3a3
 .
.
3. Винесіть множники за знак кореня:
а)
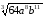 ;
б)
;
б)
 ;
в)
;
в)
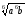 ;
г)
;
г)
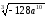 .
.
Відповідь:
а) 4a2b3
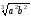 ;
б) 2|а|3|b|
;
б) 2|а|3|b|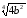 ; в) |а|
; в) |а|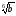 ;
г) –
4a3
;
г) –
4a3
 .
.
2. Внесення множника під знак кореня.
Перетворення, обернене до винесення множника за знак кореня, називається внесенням множника під знак кореня.
Наприклад: 2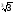 =
=
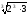 =
=
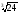 ; 3
; 3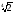 =
=
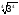 ·
·
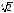 =
=
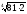 =
=
 ;
;
a
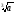 =
=
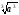 ·
·
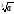 =
=
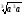 =
=
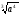 ,
якщо а
> 0;
,
якщо а
> 0;
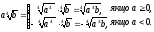
Взагалі:
-
-
Якщо а
 0, b
0, b
 0, то а
0, то а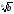 =
=
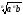 .
. -
Якщо а — довільне, то
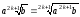 ;
;
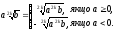
-
Виконання вправ
1. Внесіть множник під знак кореня:
а) 3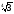 ;
б) –2
;
б) –2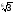 ;
в) (1 –
;
в) (1 –
 )
)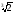 ;
г) (1 –
;
г) (1 –
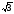 )
)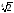 .
.
Відповідь:
а)
 ;
б) -
;
б) -
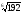 ;
в)
;
в)
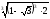 ;
г) -
;
г) -
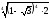 .
.
2. Внесіть множники під знак кореня, якщо а > 0, b > 0:
а) – b ;
б) аb
;
б) аb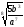 ;
в) а
;
в) а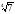 ;
г) – аb
;
г) – аb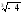 .
.
Відповідь:
а) – ;
б)
;
б)
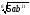 ;
в)
;
в)
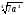 ;
г)
;
г)
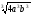 .
.
3. Внесіть множники під знак кореня:
а) а ;
б) а
;
б) а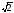 ;
в) –
аb
;
в) –
аb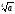 .
.
Відповідь:
а)
 ;
б)
;
б)
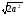 ,
якщо а
,
якщо а
 0, –
0, –
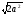 ,
якщо а
< 0;
,
якщо а
< 0;
в) –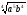 ,
якщо b
,
якщо b
 0,
0,
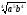 ,
якщо b
< 0.
,
якщо b
< 0.
Зведення радикалів до найпростішого вигляду, поняття подібних радикалів.
Будемо вважати, що радикал приведено до простішого вигляду, якщо: підкореневий вираз не містить дробів; раціональні множники винесено за знак кореня, показник кореня і показник степеня підкореневого виразу скорочено на їхній найбільший спільний множник.
Приклад. Приведемо радикали до простішого вигляду:
1)
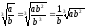 ;
2)
;
2)
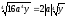 .
.
Радикали називаються подібними, якщо після приведення їх до простішого вигляду вони мають рівні підкореневі вирази і однакові показники.
Наприклад, подібними
є радикали: а)
3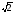 ;а
;а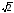 ;
;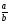
 ;
б)
5
;
б)
5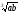 ;
;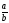
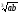 ;
(а–1)
;
(а–1)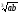 .
.
Раціональний
множник, який стоїть перед знаком
радикала, називається коефіцієнтом.
Наприклад,
3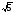 .
У цьому виразі 3 є коефіцієнтом.
.
У цьому виразі 3 є коефіцієнтом.
Щоб стверджувати, що радикали подібні чи ні, їх треба привести до простішого вигляду.
Наприклад,
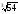 і
і
 подібні, оскільки
подібні, оскільки
 =
=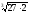 =3
=3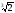 ,
а
,
а
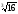 =
=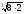 =2
=2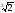 .
.
!Теорема:
Якщо а
>
b
 0, то
0, то
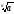 >
>
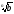 ,
тобто більшому додатному підкореневому
виразу відповідає і більше значення
кореня.
,
тобто більшому додатному підкореневому
виразу відповідає і більше значення
кореня.
Приклад.
Порівняємо числа
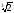 і
і
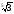 .
.
Подамо
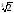 і
і
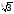 у вигляді коренів з одним і тим самим
показником:
у вигляді коренів з одним і тим самим
показником:
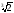 =
=
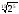 =
=
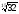 ,
а
,
а
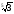 =
=
 =
=
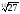 .
Згідно з доведеною теоремою, так як 32 >
27, то
.
Згідно з доведеною теоремою, так як 32 >
27, то
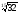 >
>
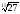 ,
а отже,
,
а отже,
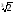 >
>
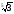 .
.
Виконання вправ
1. Порівняйте числа:
а)
 і
і
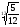 ;
б)
;
б)
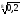 і
і
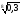 ;
в)
;
в)
 і
і
 ;
г)
;
г)
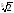 і
і
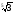 .
.
Відповідь:
а)
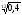 <
<
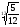 ;
б)
;
б)
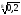 <
<
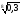 ;
в)
;
в)
 <
<
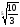 ;
г)
;
г)
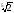 <
<
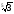 .
.
2. Що більше:
а)
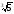 чи
чи
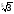 ;
б)
;
б)
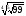 чи
чи
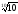 ;
в)
;
в)
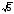 чи
чи
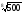 ;
г)
;
г)
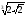 чи
чи
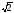 ?
?
Відповідь:
а)
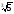 ;
б)
;
б)
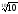 ;
в)
;
в)
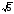 ;
г)
;
г)
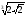 =
=
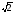 ?
?
3. Що менше: а)
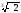 чи
чи
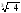 ;
б)
;
б)
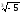 чи
чи
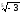 ?
?
Відповідь:
а)
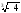 ;
б)
;
б)
 .
.
Безпосередньо з доведеної теореми випливає:
1) Якщо а
>
1,
то
 >
1 і
>
1 і
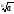 < а.
< а.
2) Якщо 0
<
а
<
1,
то
0
<
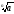 <
1 і
<
1 і
 >
а.
>
а.
3)
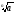 +
+
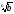 >
>
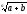 ,
при умові а
> b
,
при умові а
> b
 0, або b
> а
0, або b
> а
 0.
0.
Виконання вправ
1. Визначте знак
виразу: а)
 – 1 ; б)
– 1 ; б)
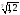 –
1; в)
–
1; в)
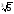 –
5; г)
–
5; г)
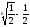 .
.
Відповідь: а) – ; б) + ; в) – ; г) + .
2. Розташуйте в порядку зростання:
а)
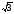 ;
;
 ;
;
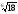 ;
б)
;
б)
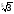 ;
;
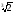 ;
;
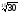 ;
в)
;
в)
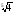 ;
;
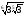 ;
;
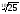 .
.
Відповідь: а)
 ;
;
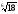 ;
;
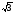 ;
б)
;
б)
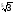 ;
;
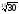 ;
;
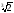 ;
в)
;
в)
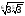 ;
;
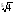 ;
;
 .
.
1. Додавання і віднімання радикалів виконується так само, як і додавання і віднімання раціональних одночленів (многочленів).
Приклади:
3 – 5
– 5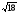 + 12
+ 12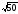 = 3·2
= 3·2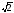 – 5·3
– 5·3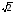 + 12·5
+ 12·5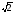 = 6
= 6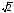 – 15
– 15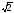 + 60
+ 60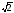 = 51
= 51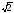 ;
;
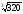 – (2
– (2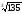 – 3
– 3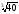 )
= 4
)
= 4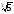 – 2·3
– 2·3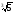 + 3·2
+ 3·2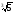 = 4
= 4 – 6
– 6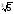 + 6
+ 6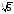 = 4
= 4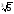 .
.
2. При множенні (діленні) радикалів з різними показниками спочатку їх треба привести до одного показника, а потім перемножити (поділити) підкореневі вирази і записати добуток (частку) під знак кореня з тим самим показником.
Приклади:
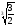 ·
·
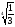 =
=
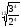 ·
·
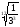 =
=
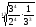 =
=
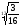 ;
;
 .
.
3. При піднесенні радикала до степеня, можна піднести до цього степеня підкореневий вираз, залишивши той самий показник кореня.
Наприклад:
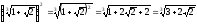 .
.
4. Щоб добути корінь із радикала, можна із підкореневого виразу добути корінь з показником, що дорівнює добутку двох даних показників.
Наприклад:
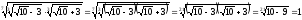 .
.
5. У деяких задачах корисно звільнятися від ірраціональних виразів у знаменнику дробу.
Звільнитися від ірраціональності в знаменнику дробу – це означає перетворити дріб, знаменник якого містить корені, до нового дробу, тотожно рівному даному, знаменник якого коренів не містить.
Якщо знаменник дробу являє собою радикал чи добуток радикала на раціональний множник, то слід чисельник і знаменник дробу домножити на таку степінь кореня того самого показника, щоб отримати степінь з показником, що дорівнює показнику кореня.
Наприклад:
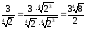 ;
;
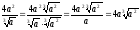 .
.
Якщо знаменник дробу є сума (або різниця) квадратних радикалів, то дріб можна привести до раціонального вигляду, помноживши чисельник і знаменник на різницю (або на суму) тих самих радикалів.
Наприклад:
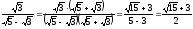 ;
;
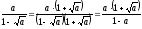 ,
якщо a
,
якщо a
 0, a
≠ l.
0, a
≠ l.
Якщо знаменник дробу є сума (різниця) кубічних радикалів, то, щоб позбутися ірраціональності в знаменнику, слід домножити чисельник і знаменник дробу на неповний квадрат різниці (суми) тих самих радикалів.
Наприклад:
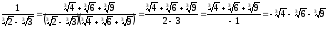 .
.
III. Підведення підсумків уроку.
IV. Домашнє завдання.
Розділ 4 § 1 Вправи № 2(а, д, є), 10(а, б).

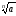 існує,
то (
існує,
то (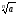 )n
= а
.
)n
= а
.