28.Степінь та Показникова функція
.docxПлан-конспект уроку
З алгебри та початків аналізу
Для групи С-21
Тема уроку. Узагальнення поняття степеня. Показникова функція, її графік і властивості.
Мета уроку: Формування поняття степеня з раціональним показником, степінь з ірраціональним показником. Засвоєння учнями поняття показникової функції, її властивостей і графіка.
Обладнання. Таблиця «Показникова функція».
Хід уроку
II. Повторення і систематизація знань учнів про степінь з натуральним і цілим показником.
Повторення і систематизацію знань учнів про степінь із натуральним і цілим показником рекомендується провести шляхом бесіди з використанням таблиці 17.
Таблиця 17
Степені
|
|
|
з натуральним показником:
а1
= а
(а
аn
= а · а · ... · а п
|
з цілим показником а0 = 1, а ≠ 0
а-n
=
|
Властивостіаm · аn = am + n аm : аn = am – n (аm)n = аmn (аb)n = anbn
|
|
III. Формування поняття:
1. Степеня з дробовим показником.
Введемо
поняття степеня з дробовим показником.
Вводячи це поняття, хотілося би, щоб
степінь з раціональним показником мав
ті самі властивості, що й степінь із
цілим показником. Зокрема, n-й
степінь числа
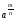 повинен дорівнювати аm.
Якщо ця властивість виконується, то
повинен дорівнювати аm.
Якщо ця властивість виконується, то
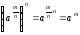 – а це означає (за означенням кореня
п-го
степеня), що число
– а це означає (за означенням кореня
п-го
степеня), що число
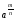 повинно бути коренем п-го
степеня із числа аn.
повинно бути коренем п-го
степеня із числа аn.
!Степенем
 числа а
> 0 з раціональним показником
числа а
> 0 з раціональним показником
 ,
де m
,
де m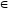 Z,
п
Z,
п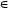 N
(п>1)
називається число
N
(п>1)
називається число
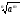 .
.
Отже,
 =
=
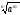 .
.
Виконання вправ
1. Подайте вирази у вигляді степеня з раціональним показником:
а)
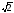 ;
б)
;
б)
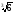 ;
в)
;
в)
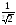 ;
г)
;
г)
 .
.
Відповідь:
а)
 ;
б)
;
б)
 ;
в)
;
в)
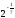 ;
г)
;
г)
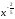 .
.
2. Подайте вирази у вигляді кореня із числа чи виразу:
а)
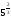 ;
б) 5
;
б) 5 ;
в) 6
;
в) 6 ;
г) 3
;
г) 3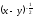 .
.
Відповідь:
а)
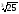 ;
б)
;
б)
 ; в)
; в)
 ;
г)
;
г)
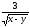 .
.
3. Обчисліть:
а)
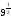 ;
б)
;
б)
 ;
в)
;
в)
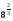 ;
г)
;
г)
 .
.
Відповідь: а) 3; б) 3; в) 4; г) 27.
2. Вивчення властивостей степенів з раціональним показником.
Для будь-яких раціональних чисел р і q і будь-яких додатних а і b справедливі рівності:
|
аp · аq = ap +q; аp : аq = ap – q ; (аp)q = аpq ; (аb)p = apbp;
|
Для
доведення цих властивостей треба
скористатися означенням степеня з
раціональним показником і властивостями
коренів. Доведемо першу рівність: нехай
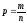 ,
,
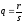 ,
тоді
,
тоді
 Останні
рівності доводяться аналогічно.
Останні
рівності доводяться аналогічно.
Виконання вправ: №283, 286.
3. Сприймання поняття про степінь з ірраціональним показником.
Розглянемо
степінь
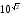 з ірраціональним показником
з ірраціональним показником
 .
Ірраціональне число
.
Ірраціональне число
 можна подати у вигляді нескінченного
неперіодичного десяткового дробу.
можна подати у вигляді нескінченного
неперіодичного десяткового дробу.
Розглянемо
послідовність наближень числа
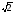 :
:
1 <
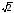 < 2,
< 2,
1,4 <
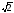 <
1,5,
<
1,5,
1,41 <
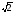 < 1,42,
< 1,42,
1,414 <
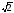 < 1,415,
< 1,415,
1,4142 <
 < 1,4143,
< 1,4143,
…
За допомогою калькулятора знайдемо наближені значення степенів числа 10 з недостачею і надлишком, тоді матимемо:
10 = 101
<
 < 102
= 100,
< 102
= 100,
25,119
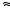 101,4
<
101,4
<
 < 101,5
< 101,5
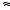 31,623,
31,623,
25,704
 101,41
<
101,41
<
 < 101,42
< 101,42
 26,303,
26,303,
25,942
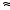 101,414
<
101,414
<
 < 101,415
< 101,415
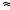 26,002 ,
26,002 ,
25,953
 101,4142
<
101,4142
<
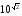 < 101,4143
< 101,4143
 25,960 ,
25,960 ,
Наведені
значення з недостачею і надлишком
наближаються до одного і того самого
числа
 = 25,9..., яке і прийнято вважати степенем
числа 10 з показником
= 25,9..., яке і прийнято вважати степенем
числа 10 з показником
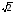 .
.
Таким чином, ми розширили поняття степеня на будь-які дійсні показники, зберігаючи при цьому властивості степенів.
4. Сприймання поняття про показникові функцію.
!Функція виду у = ах, де а > 0, а ≠ 1, називається показниковою (з основою а).
Властивості показникової функції записати в робочому зошиті у вигляді таблиці 19
Таблиця 19
|
Показникова функція у = ах, а > 0, а ≠ 1
|
|
|
а > 1 |
0 < а < 1 |
|
1. D(y) = R
2. Е(у)
= (0; +
3. Зростає
x1
> x2
4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у < 1 6. Якщо х > 0, то у > 1
|
1. D(y) = R
2. E(y)
= (0; + 3. Спадає
x1
> x2
4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у > 1 6. Якщо х > 0, то у < 1
|
Враховуючи вищезазначене, можна зробити висновки.
1. Область
визначення показникової функції —
множина R
дійсних чисел, бо степінь aх,
де а
>
0, визначений для всіх х
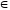 R.
R.
2. Множина значень показникової функції — множина всіх додатних дійсних чисел.
3. Показникова функція у = aх є зростаючою на множині дійсних чисел, якщо а > 1, і спадною, якщо 0 < а < 1.
4. Якщо х = 0, то у = а° = 1.
5. Якщо х > 0, то у > 1, якщо а > 1, і у < 1, якщо 0 < а < 1.
6. Якщо х < 0, то у < 1, якщо а > 1, і у > 1, якщо 0 < а < 1.
7. Графіком показникової функції є крива, яка називається експонентою.
Усне виконання вправ
1. Які із поданих функцій є показниковими:
а) у
= 2х;
б) у
= х3;
в) у
= (-5)х;
г) у
=
( )х;
д) у
=
(0,3)х;
е)
у
= πх?
)х;
д) у
=
(0,3)х;
е)
у
= πх?
Відповідь: а); г); д); е).
2. Наведіть приклади показникових функцій.
Почнемо
вивчення показникових функцій з функції
у
= 2х.
Складемо
таблицю значень функції:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у = 2х |
|
|
|
1 |
2 |
4 |
8 |
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у = 2х (рис. 142).
Показникова функція у = 2х має властивості:
1. Область визначення — множина всіх дійсних чисел.
2. Область значень — множина всіх додатних чисел.
3. Функція у = 2х — зростаюча на множині всіх дійсних чисел.
4. Графік функції перетинає вісь у в точці(0; 1).
Усне виконання вправ
1. Чи є серед значень функції у = 2х:
а) найбільше; б) найменше? Відповідь: ні.
2. Порівняйте значення виразів:
а)
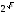 і
і
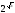 ;
б) 2-3
і 2-4;
в)
;
б) 2-3
і 2-4;
в)
 і
і
 .
.
Відповідь:
а)
 <
<
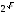 ;
б) 2-3
> 2-4;
в)
;
б) 2-3
> 2-4;
в)
 >
>
 .
.
3.
Розташуйте числа
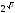 ;
;
 ;
;
 ;
;
 ;
;
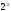 у порядку зростання.
у порядку зростання.
Відповідь:
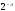 ;
;
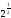 ;
;
 ;
;
 ;
;
 .
.
4. Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 2х > 2у; б) 2х < 2у. Відповідь: а) х > у; б) х < у.
5. На рисунку 86 із підручника зображено графіки функцій у = 2х і у = 3х. Чим відрізняються ці функції? Їхні графіки?
Відповідь: ці функції мають одинакові властивості, функція у = 3х зростає більш швидше (графік цієї функції піднімається вгору більш круто).
2. Порівняйте значення виразів:
а)
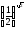 і
і
 ;
б)
;
б)
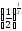 і
і
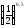 ;
в)
;
в)
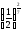 і
і
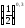 ;
г)
;
г)
 і
і
 ;
д)
;
д)
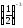 і
і
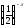 .
.
Відповідь:
а)
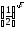 >
> ;
б)
;
б)
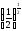 =
=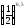 ;
в)
;
в)
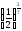 >
> ;
г)
;
г)
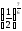 <
< ;
д)
;
д)
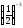 <
<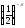 .
.
3.
Розташуйте числа
 ,
,
 ,
,
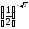 ,
,
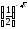 ,
,
 у
порядку зростання.
у
порядку зростання.
Відповідь:
 ,
,
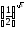 ,
,
 ,
,
 ,
,
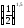 .
.
4.
Порівняйте х
і
у,
якщо відомо, що вірна нерівність: а) >
> ;
б)
;
б) >
> ;
;
Відповідь: а) х < у; б) х > у.
5. Чим
відрізняються властивості і графіки
функцій у
= і
у=
і
у=
 ?
?
Відповідь:
вони мають однакові властивості, функція
у
=
 спадає
більш швидше.
спадає
більш швидше.
Усне виконання вправ
1. Які з наведених показникових функцій є зростаючими, а які — спадними:
а) y
= πx
;
б) y
= (0,5)x;
в)
у =
 ;
г)
y
= 2-x.
;
г)
y
= 2-x.
2. Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 0,02х < 0,02y; б) πx > πy.
Відповідь: а) х > у; б) x < у.
3. Порівняйте основу а > 0 з одиницею, якщо відомо, що вірна нерівність:
а) а10 > а15; б) а10 < а15.
Відповідь: а) а > 1; б) 0 < а < 1.
V. Підсумок уроку.
VI. Домашнє завдання.
-
Побудувати графік функції у =
 .
. -
Порівняйте значення виразів:
а)
 i
i
 ;
б)
;
б)
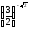 і
і
 .
.

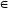 R)
R)
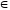 N,
п > 2
N,
п > 2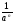 ,
а
≠
0, n
,
а
≠
0, n
 N
N
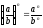 ;
;

 .
.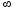 )
)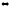
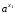 >
>
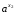
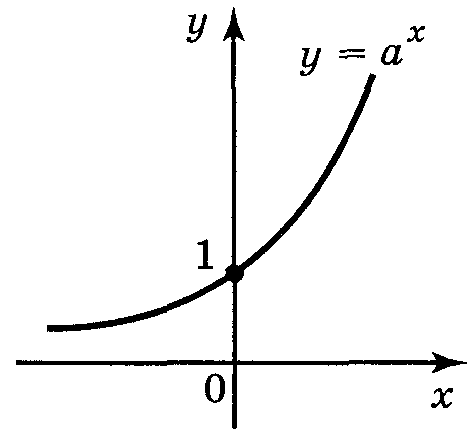
 ).
).
 <
<