
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ 6
.1.docІНДИВІДУАЛЬНЕ ЗАВДАННЯ 6.1
Поверхні другого порядку. Загальна теорія поверхонь другого порядку. Геометричні перетворення простору.
Задачі, з яких складається робота.
|
№ варіантів |
Номери задач індивідуального завдання. |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
1 |
3 |
10 |
48 |
58 |
|
2 |
2 |
11 |
31 |
41 |
52 |
|
3 |
3 |
12 |
32 |
42 |
59 |
|
4 |
1 |
4 |
13 |
28 |
39 |
|
5 |
2 |
5 |
29 |
34 |
55 |
|
6 |
3 |
6 |
30 |
35 |
56 |
|
7 |
4 |
7 |
31 |
36 |
57 |
|
8 |
5 |
8 |
32 |
37 |
58 |
|
9 |
6 |
9 |
33 |
38 |
59 |
|
10 |
7 |
10 |
34 |
39 |
59 |
|
11 |
1 |
8 |
11 |
35 |
40 |
|
12 |
2 |
9 |
12 |
36 |
41 |
|
13 |
3 |
10 |
13 |
37 |
42 |
|
14 |
4 |
11 |
14 |
38 |
43 |
|
15 |
5 |
12 |
15 |
39 |
44 |
|
16 |
6 |
13 |
16 |
40 |
45 |
|
17 |
7 |
14 |
17 |
41 |
46 |
|
18 |
8 |
15 |
18 |
42 |
47 |
|
19 |
9 |
16 |
19 |
43 |
48 |
|
20 |
10 |
17 |
20 |
44 |
56 |
|
21 |
11 |
18 |
22 |
45 |
57 |
|
22 |
12 |
19 |
23 |
46 |
58 |
|
23 |
13 |
20 |
24 |
47 |
59 |
|
24 |
14 |
21 |
25 |
48 |
59 |
|
25 |
15 |
22 |
26 |
49 |
58 |
|
26 |
16 |
23 |
27 |
50 |
59 |
|
27 |
17 |
24 |
28 |
51 |
56 |
|
28 |
18 |
25 |
29 |
52 |
57 |
|
29 |
19 |
26 |
30 |
53 |
59 |
|
30 |
1 |
27 |
31 |
54 |
59 |
-
Скласти рівняння кругової циліндричної поверхні, якщо відомі параметричні рівняння її осі x=3t+1, у=-2t-2, z=t+2 і точка М(2;-1;1), яка належить шуканій поверхні.
-
Скласти рівняння поверхні, утвореної обертанням навколо осі ОУ заданих кривих, які належать площині ХОУ:
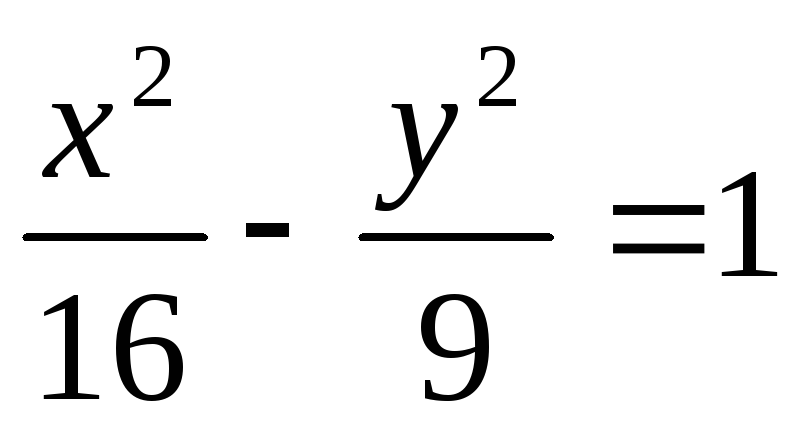 .
. -
Скласти рівняння поверхні, утвореної обертанням навколо осі ОУ заданих кривих, які належать площині ХОУ: х2=6у.
-
Записати рівняння еліпсоїда, осі якого співпадають з осями координат і який проходить через точку М(2;0;1) і перетинає площину ХОУ по еліпсу
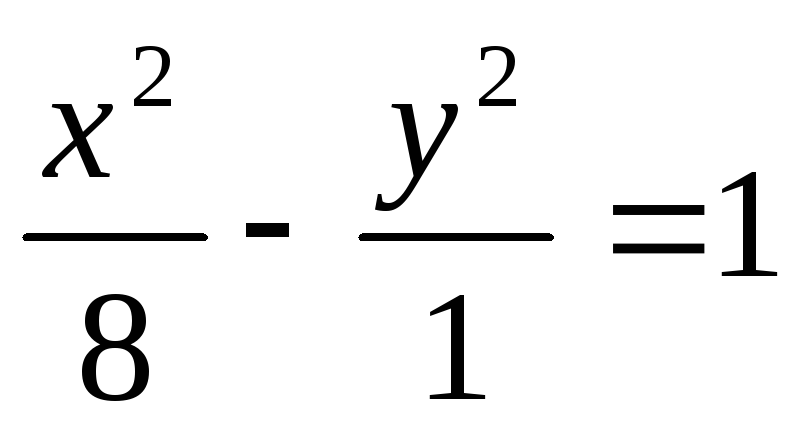 .
. -
Скласти рівняння циліндричної поверхні обертання радіуса R=3, якщо її вісь обертання проходить через початок координат і паралельна даному вектору
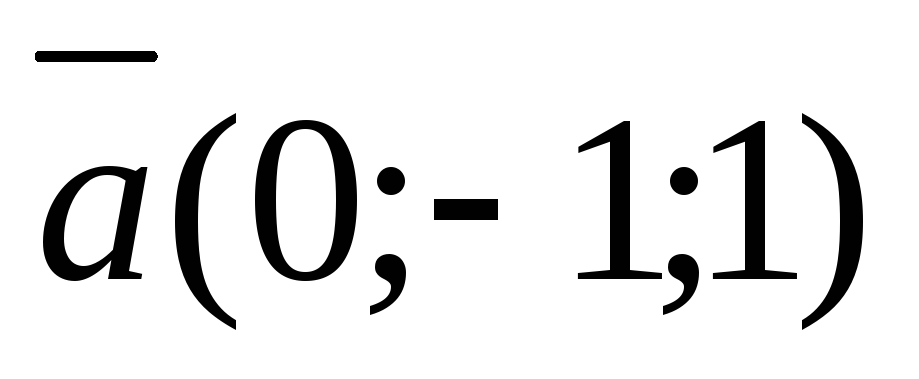 .
. -
Скласти рівняння кругової конічної поверхні, вершина якої знаходиться в точці S(1;2;3), вісь перпендикулярна до даної площини 2х+2у-z+1=0.
-
Скласти рівняння циліндричної поверхні, твірні якої паралельні прямій
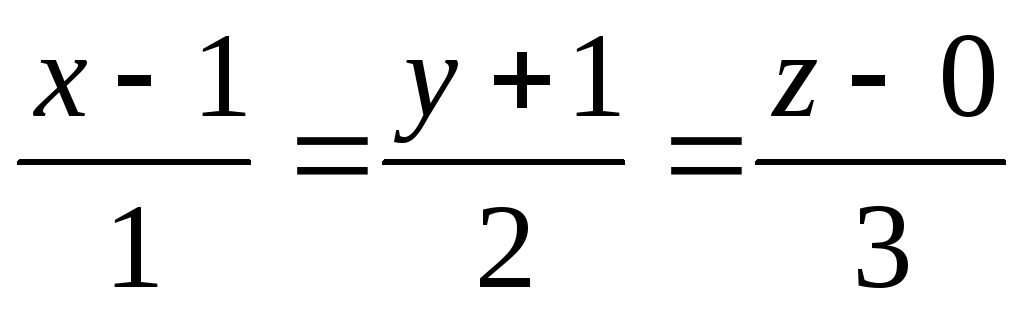 ,
рівняння прямолінійних твірних поверхні
,
рівняння прямолінійних твірних поверхні
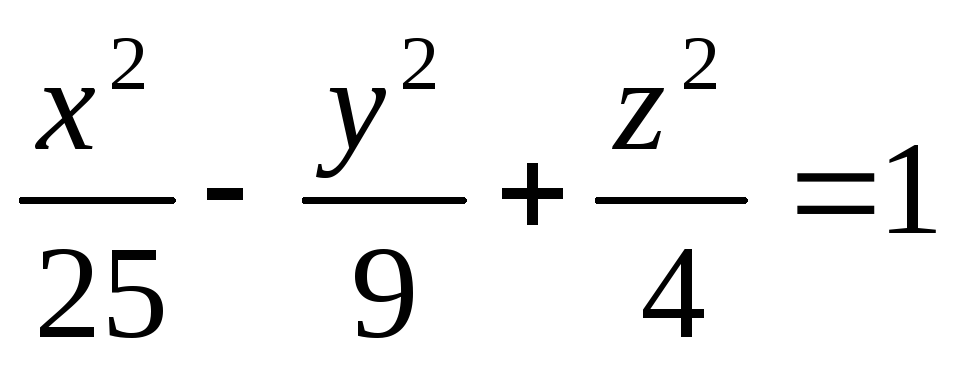 ,
які проходять через
точку
М(5;3;2).
,
які проходять через
точку
М(5;3;2). -
Написати рівняння сфери, яка проходить через точку .М(3;3;-1 ) і дотикається до даної площини 2х-2у-z+5=0 в точці
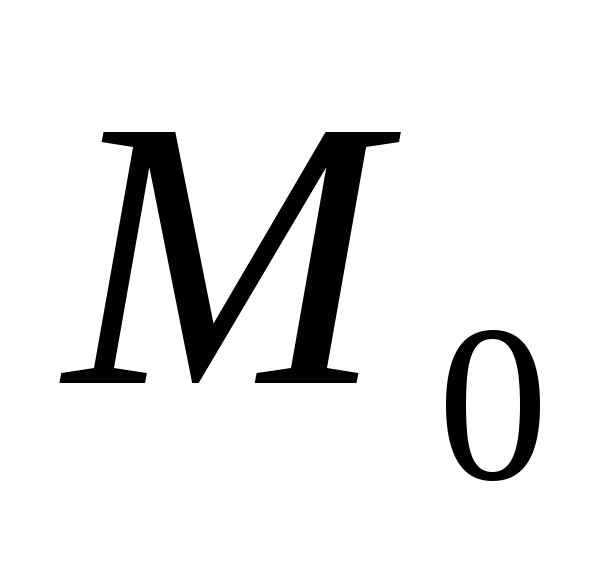 (-1;1; 1).
(-1;1; 1). -
Скласти рівняння циліндричної поверхні, направляюча якої лежить в площині ХОУ і має рівняння
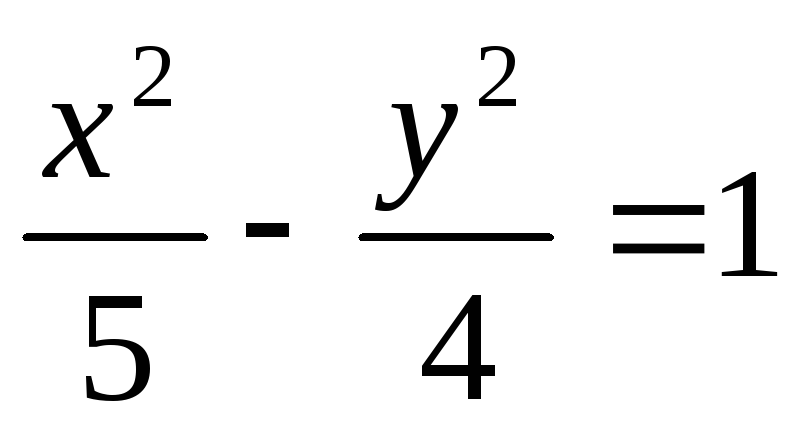 ,
а її твірні паралельні, даному а
направляючою є лінія
,
а її твірні паралельні, даному а
направляючою є лінія
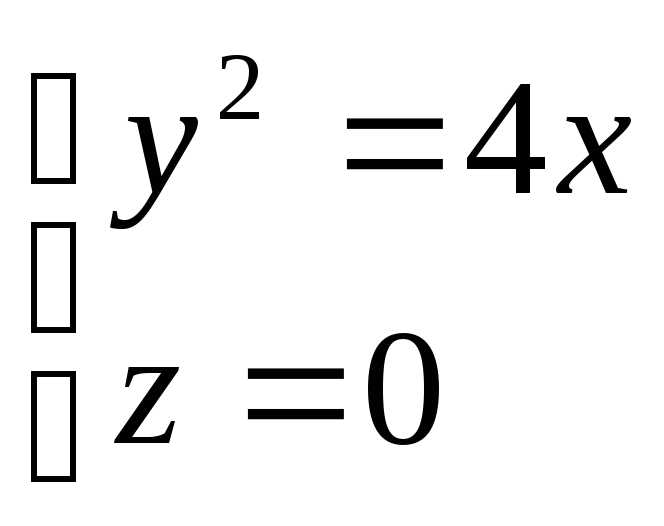 .
. -
Скласти рівняння конічної поверхні, якщо направляючу в площині ХОУ задано рівнянням
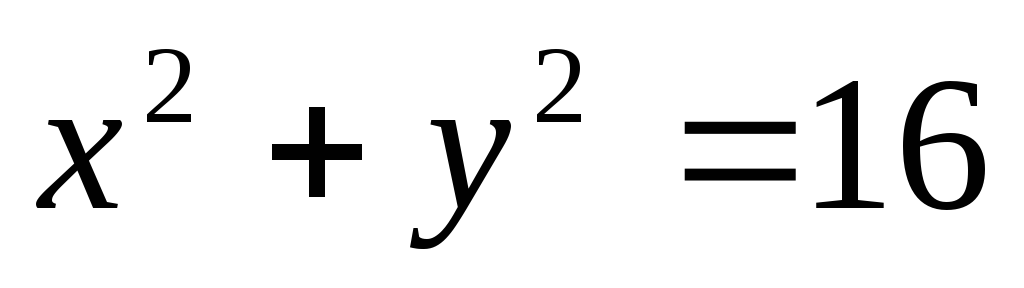 ,
а її вершина лежить в даній точці S
(0;0;1).
,
а її вершина лежить в даній точці S
(0;0;1). -
Дослідити методом перерізів поверхню другого порядку в прямокутній Декартові системі координат:
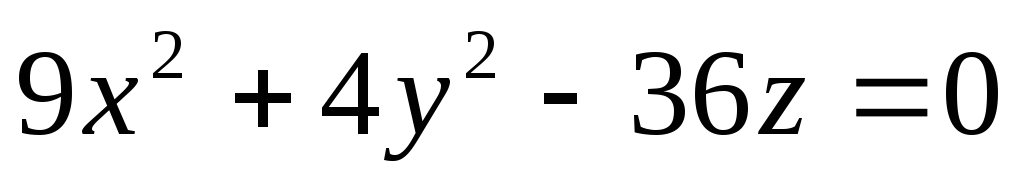 .
Зробити малюнок.
.
Зробити малюнок. -
Знайти кут між прямолінійними твірними поверхні
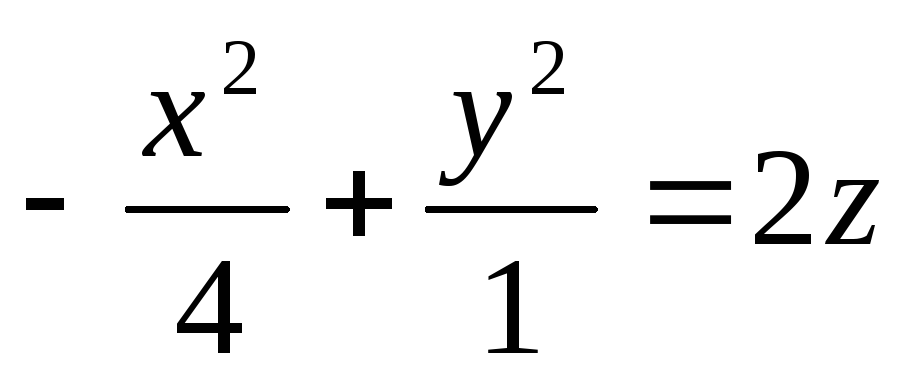 в
даній точці
в
даній точці
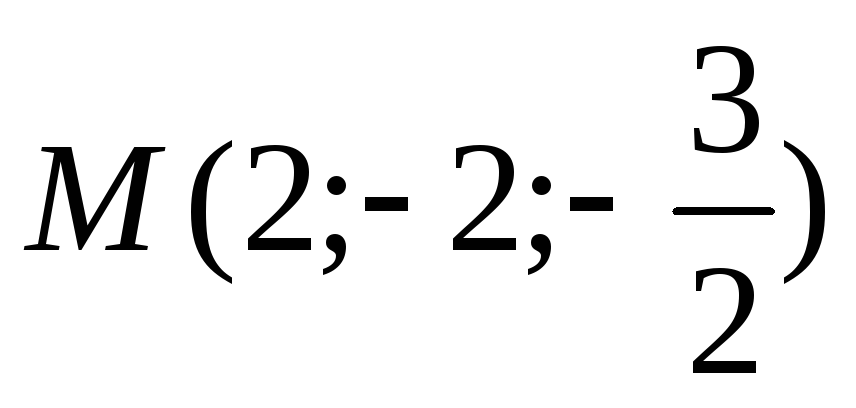
-
Скласти рівняння конічної поверхні, яка проектує даний еліпс
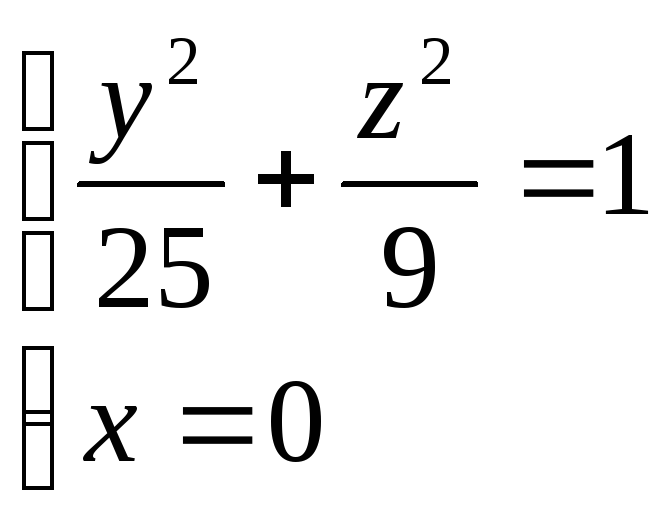 з точки
S(4;0;-3).
з точки
S(4;0;-3).
-
Скласти рівняння конічної поверхні, вершина якої знаходиться в початку координат,
направляючу
лінію якої задано рівняннями:
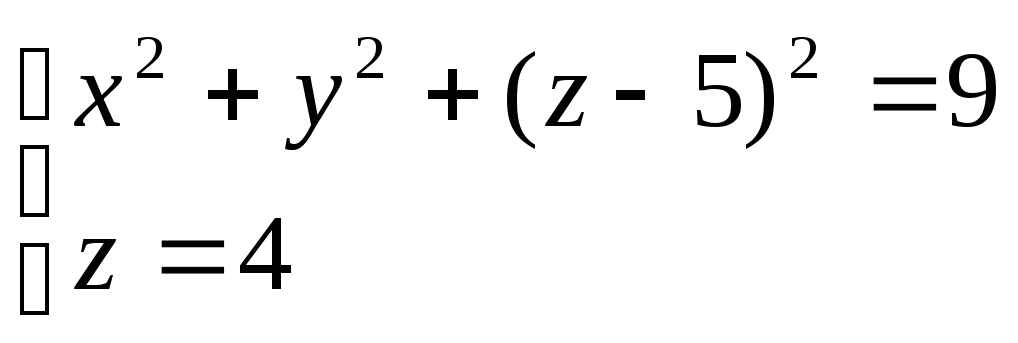 .
.
-
Направляючу циліндричної поверхні задано рівнянням
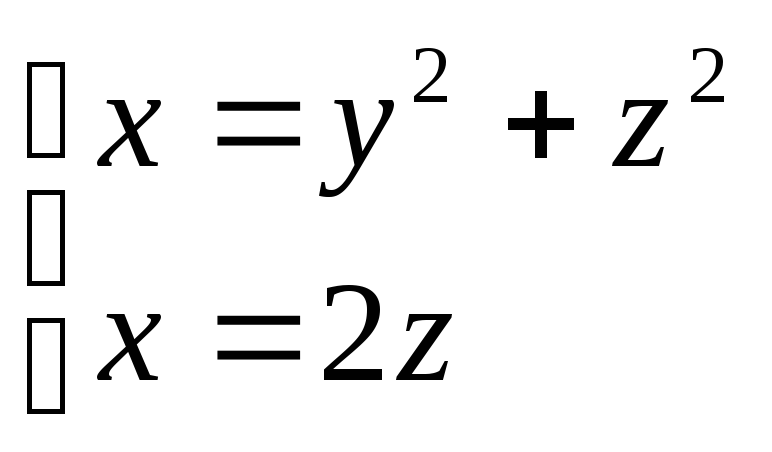 ,
а його твірна
перпендикулярна
до площини направляючої. Скласти
рівняння циліндричної поверхні.
,
а його твірна
перпендикулярна
до площини направляючої. Скласти
рівняння циліндричної поверхні. -
Направляюча пряма конуса задана рівнянням
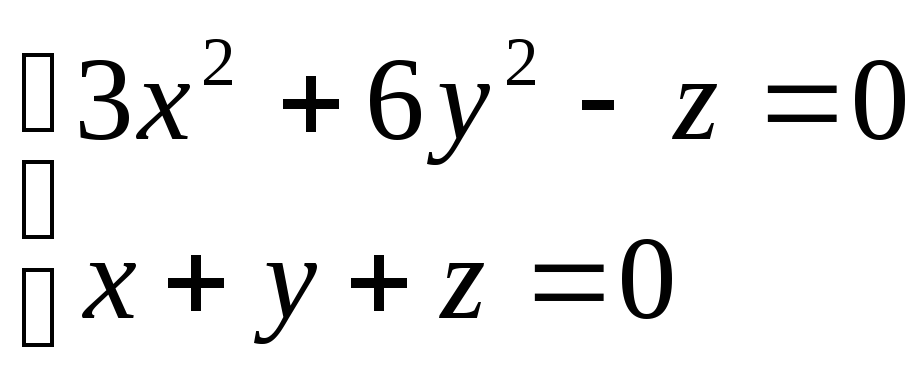 ,
а вершина конуса
знаходиться
в точці S(-3;0;0).
Скласти рівняння конічної поверхні.
,
а вершина конуса
знаходиться
в точці S(-3;0;0).
Скласти рівняння конічної поверхні. -
Скласти рівняння конічної поверхні, вершина якої знаходиться в точці О(0;0;0), а направляюча пряма задана рівняннями:
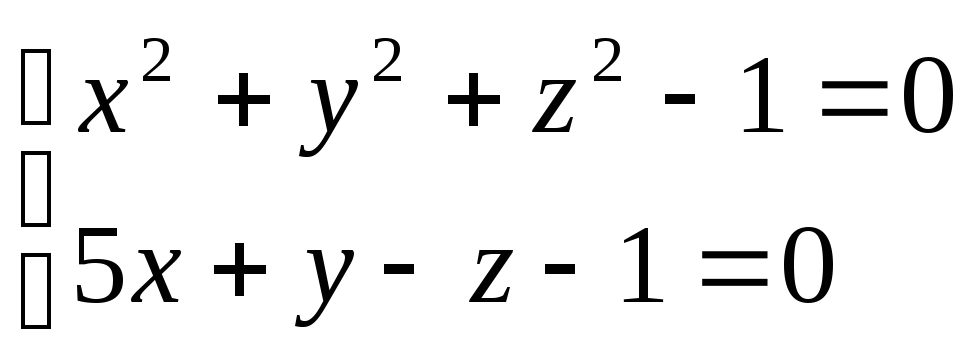 .
. -
Скласти рівняння конічної поверхні, вершина якої знаходиться в точці S(0;0;3), а направляюча пряма задана рівняннями:
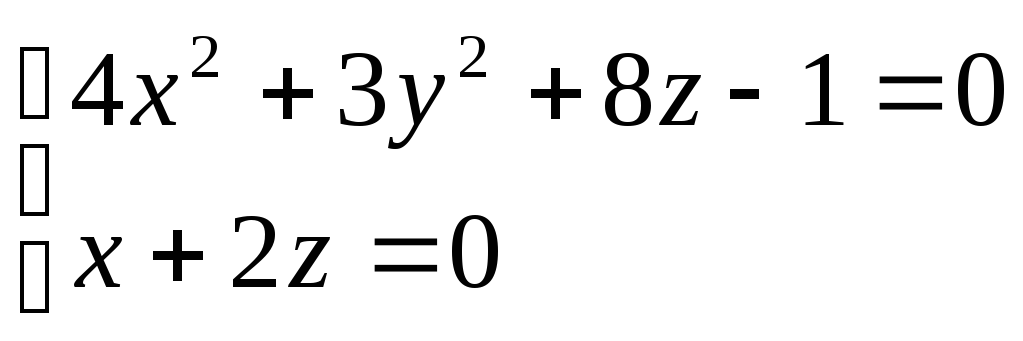 .
. -
Скласти рівнянням конуса з вершиною в початку координат, твірні якого дотикаються до сфери
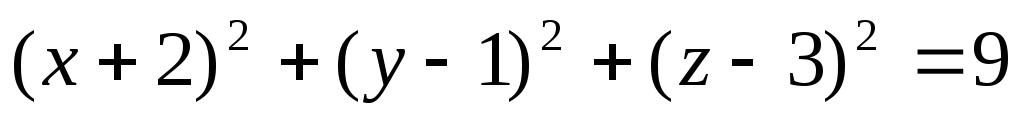 .
. -
Пряма
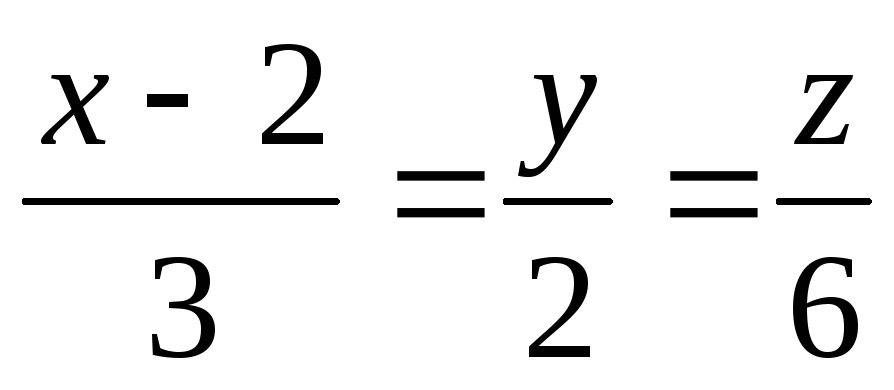 обертається
навколо осі ОХ. Знайти рівняння
поверхні
обертання.
обертається
навколо осі ОХ. Знайти рівняння
поверхні
обертання. -
Скласти рівняння поверхні, яку можна одержати при обертанні навколо осі OZ, бісектрис координатних кутів площини YОZ.
-
Скласти рівняння циліндричної поверхні, направляюча пряма якої є лінія
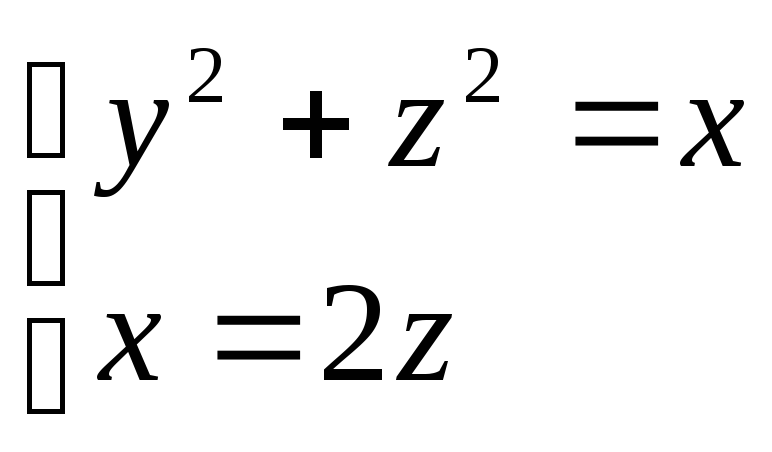 , а
твірна
перпендикулярна площині, в якій лежить
направляюча.
, а
твірна
перпендикулярна площині, в якій лежить
направляюча. -
Скласти рівняння циліндричної поверхні, направляюча лінія якої задана
рівняннями:
 , якщо її твірні перпендикулярні до
площини,
в
якій лежить направляюча лінія.
, якщо її твірні перпендикулярні до
площини,
в
якій лежить направляюча лінія.
-
Скласти рівняння циліндричної поверхні, твірні якої паралельні прямій
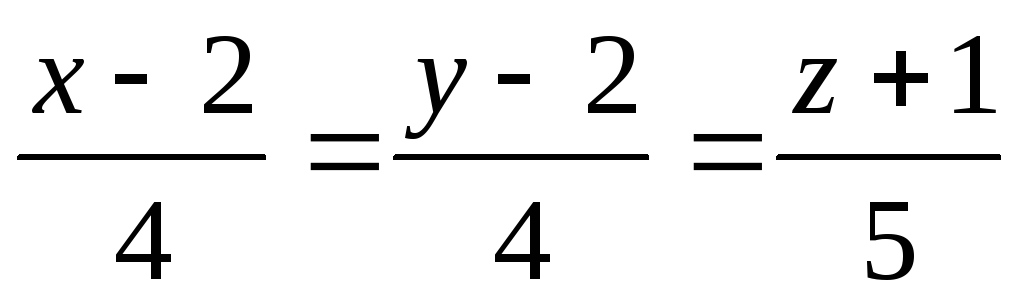 ,
а її направляюча лінія задана рівняннями:
,
а її направляюча лінія задана рівняннями:
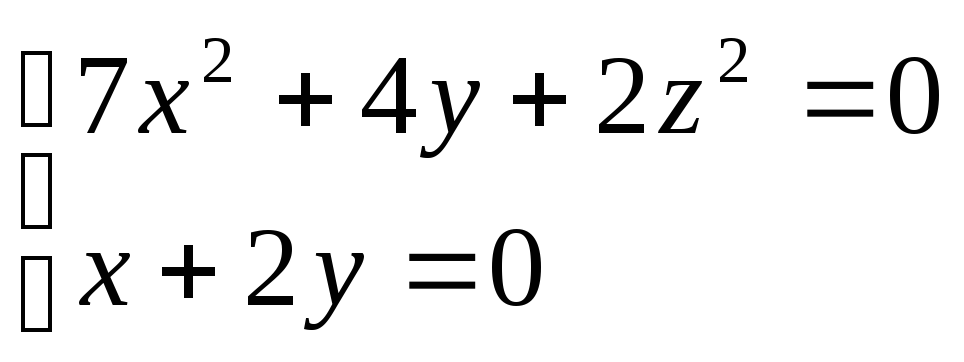 .
. -
Скласти рівняння сфер, які вписані в циліндричну поверхню, яка задана рівнянням
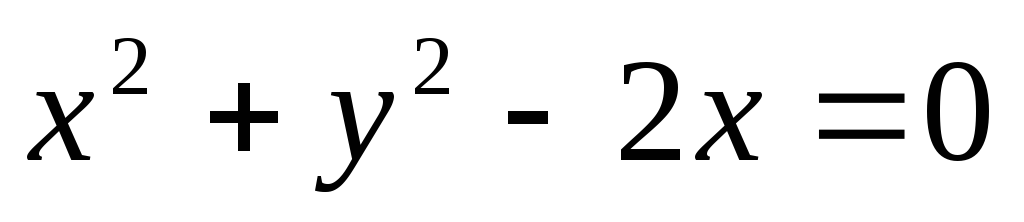 ,
і які дотикаються до площини Зх-6у-2z+6=0.
,
і які дотикаються до площини Зх-6у-2z+6=0. -
Скласти рівняння сфер, вписаних в циліндричну поверхню х2+у2=1 , які дотикаються до площини
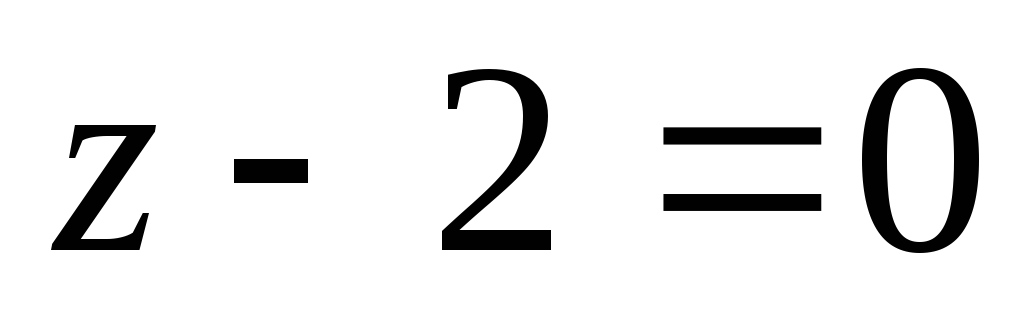 .
. -
Знайти множину точок, для кожної з яких модуль різниці віддалей від двох даних точок
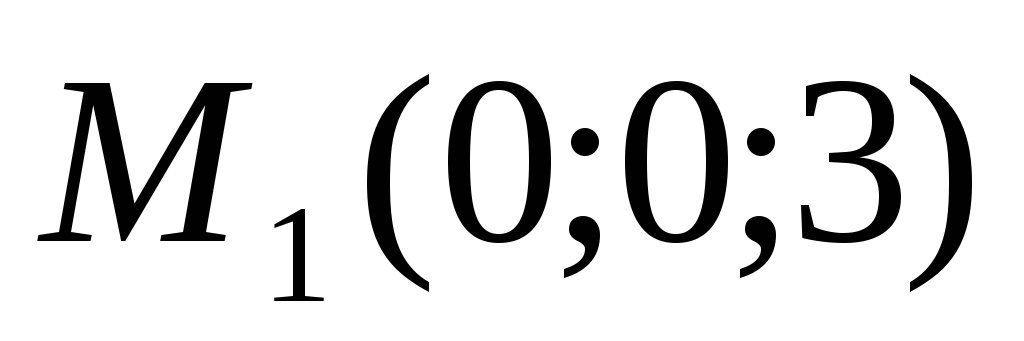 та
та
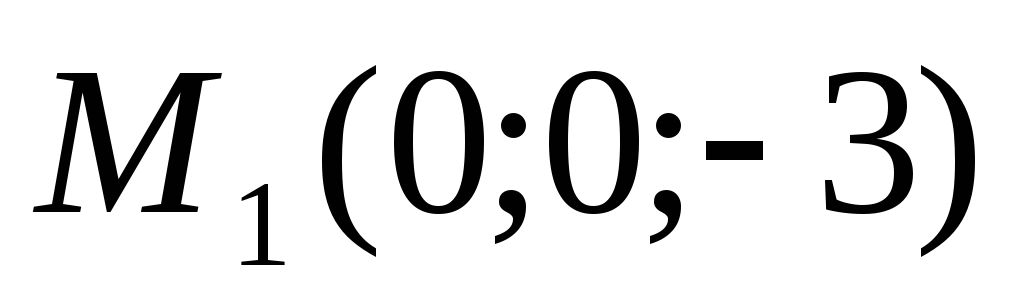 є
величина стала, яка дорівнює 4.
є
величина стала, яка дорівнює 4. -
Знайти центр і радіус кола:
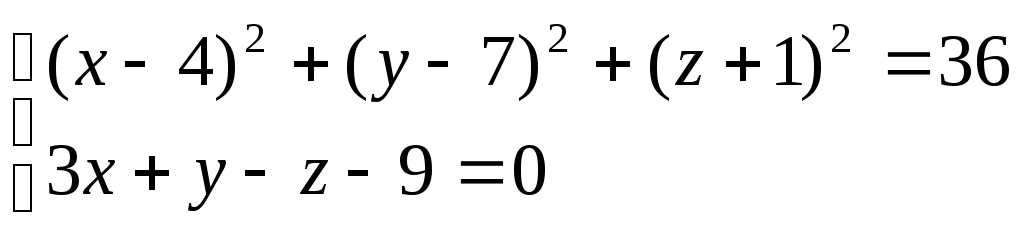 .
. -
Скласти рівняння поверхні, яка утворюється при обертанні даного еліпса навколо більшої осі. Еліпс лежить в площині Х0Z, його центр співпадає з початком координат, мала вісь дорівнює 8, ексцентриситет дорівнює
 .
. -
Скласти рівняння двопорожнинного гіперболоїда, яким можна одержати при обертанні гіперболи:
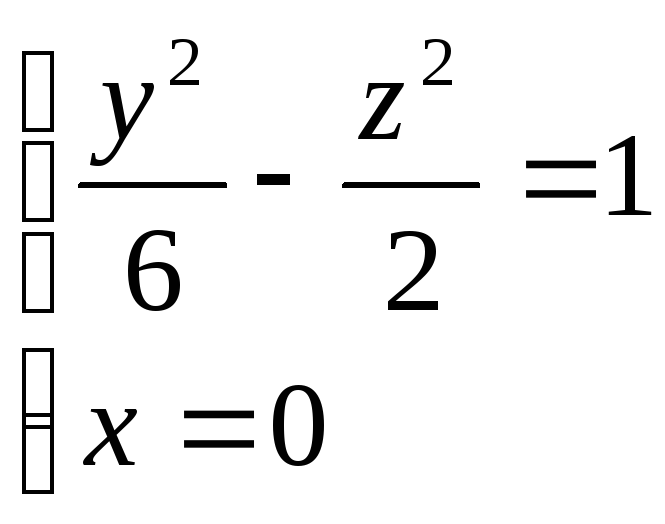 .
. -
Скласти рівняння однопорожнинного гіперболоїда, який можна одержати при обертанні гіперболи в
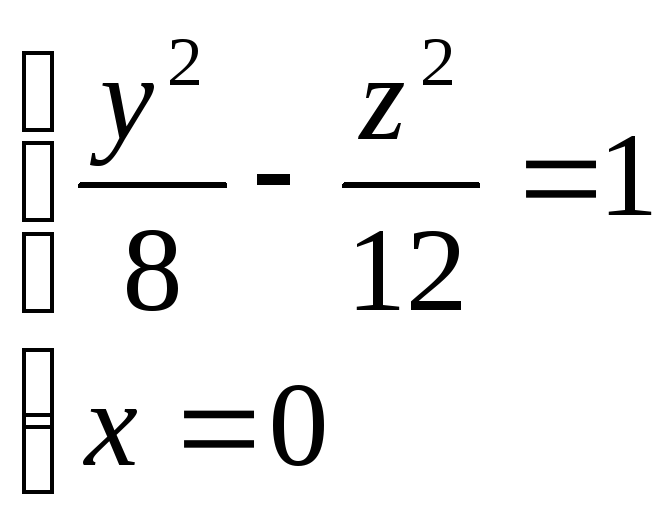 .
. -
Знайти прямолінійні твірні гіперболічного параболоїда
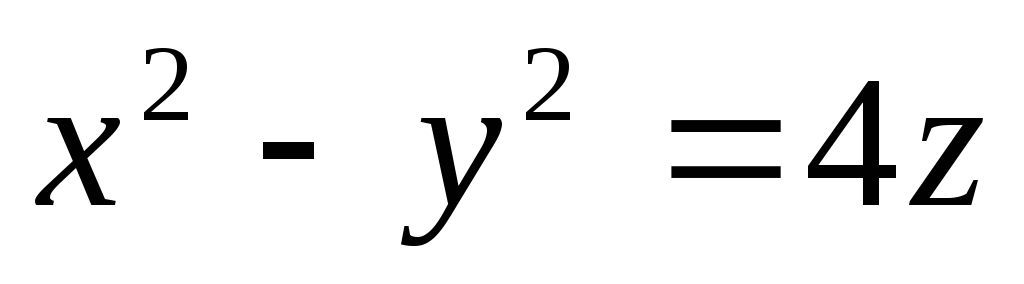 ,
які паралельні даній площині
,
які паралельні даній площині
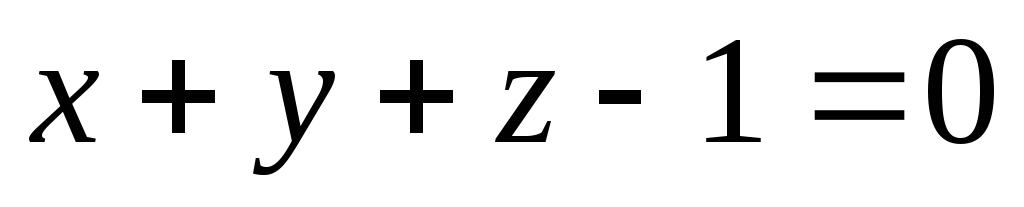 .
. -
Знайти прямолінійні твірні гіперболоїда
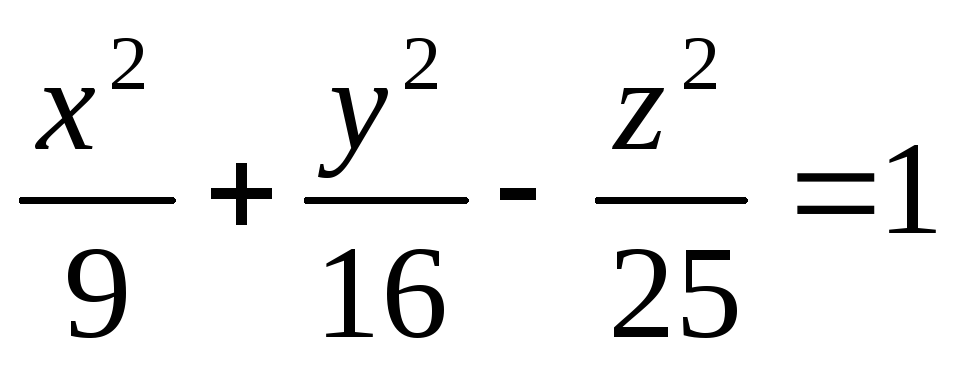 ,
які проходять через
точку
М(6;2;8).
,
які проходять через
точку
М(6;2;8). -
Знайти прямі, які проходять через точку А(4;0;2) і належать поверхні
 .
. -
Знайти геометричне місце дотичних, які проведені з початку координат до сфери
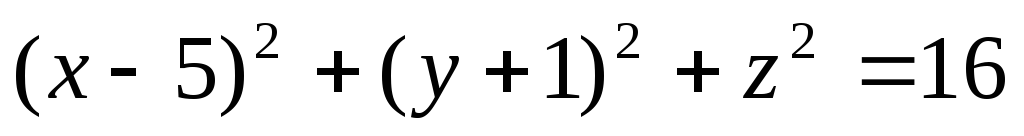 .
. -
Скласти рівняння циліндричної поверхні, напрямна якої є колом х2+у2=25, z=0, а твірна паралельна вектору {5,3,2}.
-
Скласти рівняння циліндричної поверхні, твірні якої паралельні вектору {2,4,-3}, а напрямна задана рівняннями х2+z2=9, y=1.
-
Скласти рівняння циліндричної поверхні, напрямна якої задана рівняннями
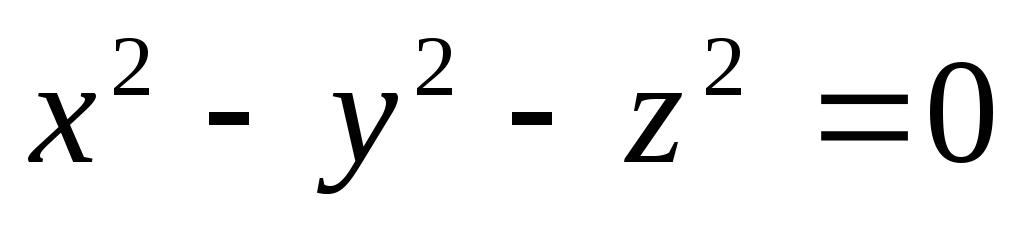 ,
,
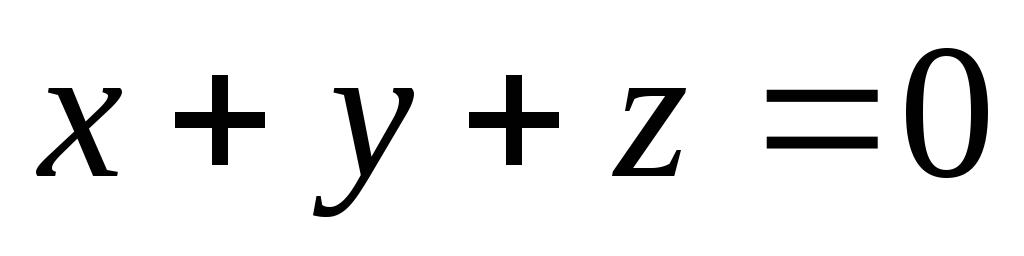 ,
а твірні перпендикулярні до площини
напрямної.
,
а твірні перпендикулярні до площини
напрямної. -
3найти рівняння циліндричної поверхні, знаючи, що вона проходить через криву
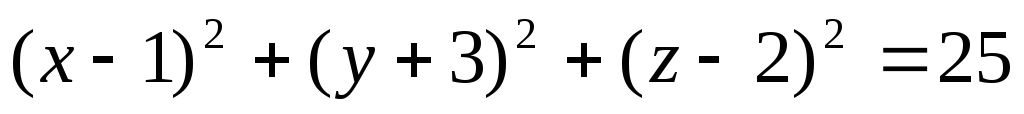 ,
,
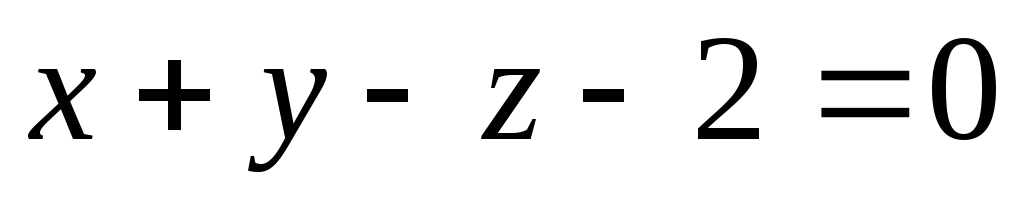 ,
а її твірна:
,
а її твірна:
а) паралельна осі Ох;
б) паралельна прямій х=у, z=1.
-
Циліндрична поверхня, твірні якої перпендикулярні до площини
 ,
описана навколо сфери
,
описана навколо сфери
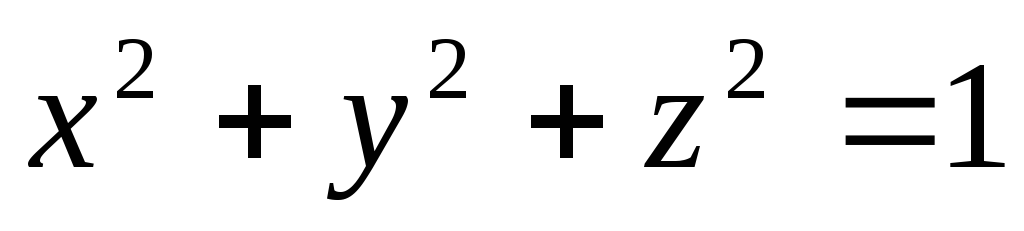 .
Скласти рівняння цієї циліндричної
поверхні.
.
Скласти рівняння цієї циліндричної
поверхні. -
Циліндрична поверхня, твірні якої паралельні прямій x=2t-3, у=-t+7, z=-2t+5, описана навколо сфери
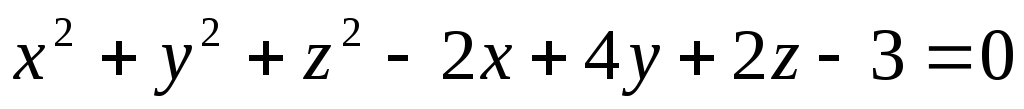 .
Скласти
рівняння цієї циліндричної поверхні.
.
Скласти
рівняння цієї циліндричної поверхні. -
Записати рівняння циліндричної поверхні, описаної навколо сфери
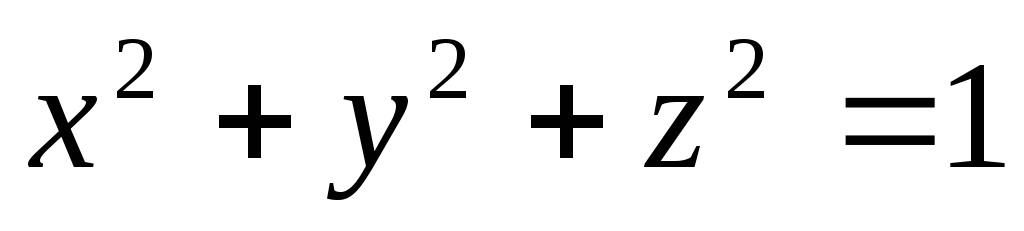 ,
якщо її твірна утворює рівні кути з
осями координат.
,
якщо її твірна утворює рівні кути з
осями координат. -
Скласти рівняння описаної навколо сфери
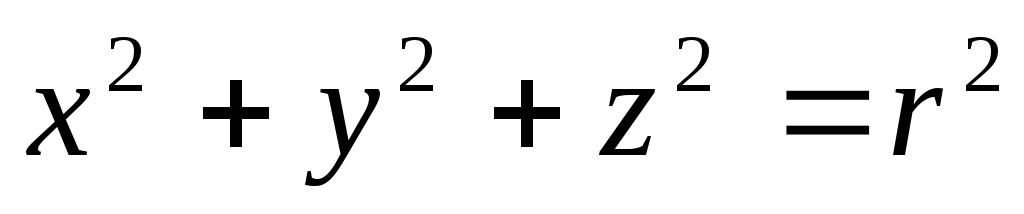 циліндричної
поверхні, твірні якої паралельні вектору
циліндричної
поверхні, твірні якої паралельні вектору
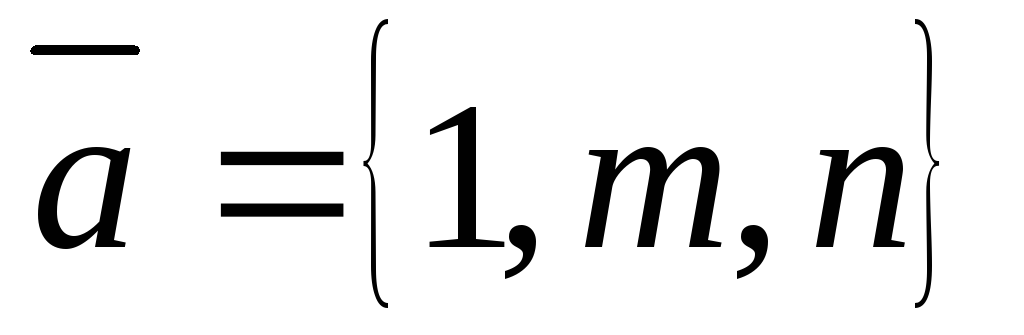 .
. -
Скласти рівняння кругової циліндричної поверхні, яка проходить через точку (2, -1,1), якщо її віссю є пряма х = 3t+1, у = -2t-2, z= t+ 2.
-
Скласти рівняння кругової циліндричної поверхні, яка проходить через точку (1,-2,1), якщо її віссю є пряма
 .
. -
Скласти рівняння конічної поверхні з вершиною в початку координат, напрямна якої задана рівняннями
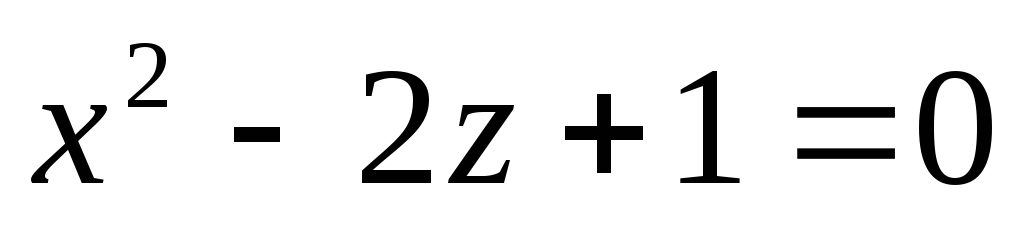 ,
у-z+1
=0.
,
у-z+1
=0. -
Скласти рівняння конічної поверхні, вершина якої знаходиться в точці (3,-1, -2), а напрямна задана рівняннями х2 +у2 + z2 = 1, х-у + z = 0.
-
Скласти рівняння конічної поверхні, вершина якої знаходиться в початку координат, а напрямна задана рівняннями х2 + у2 + (z-5)2 = 9, z = 4.
-
Скласти рівняння конічної поверхні з вершиною в точці (0,0,8), якщо її напрямною є парабола у2 =4х, z= 0.
-
Напрямна конічної поверхні задана рівняннями 3х2 +6у2 -z = 0, х + у + z = 1, а її вершина знаходиться в точці (-3,0,0). Скласти рівняння цієї конічної поверхні.
-
Вісь ОZ є віссю кругової конічної поверхні з вершиною в початку координат. Скласти рівняння цієї конічної поверхні, якщо вона проходить через точку (3, -4, 7).
-
Пряма
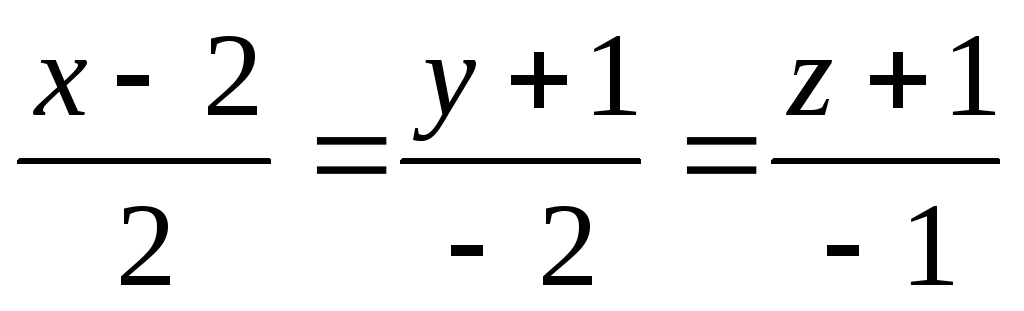 є
віссю кругової конічної поверхні,
вершина якої лежить у площині OYZ.
Скласти рівняння цієї конічної поверхні,
знаючи, що їй належить точка
є
віссю кругової конічної поверхні,
вершина якої лежить у площині OYZ.
Скласти рівняння цієї конічної поверхні,
знаючи, що їй належить точка
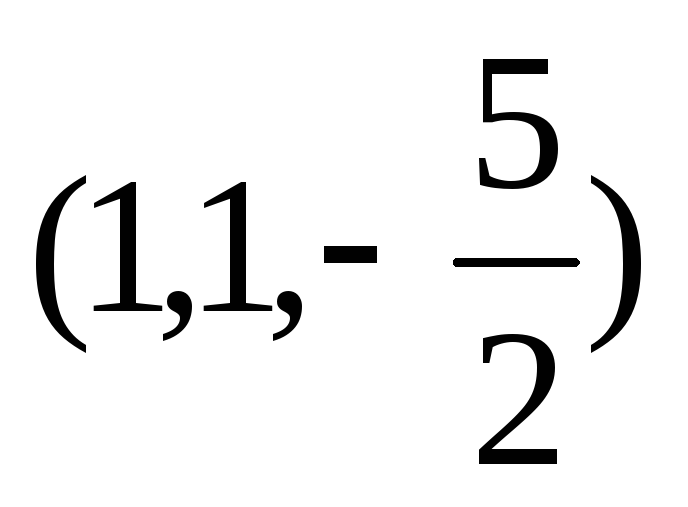 .
. -
Скласти рівняння конічної поверхні з вершиною в точці (5,0,0), твірні якої дотикаються до сфери х2 + у2 + z2 = 9.
-
Скласти рівняння конічної поверхні з вершиною в початку координат, твірні якої дотикаються до сфери (х + 2)2 + (у -1)2 + (z -3)2 = 9.
-
Знайти геометричне місце прямих, що проходять через точку (3,0, 5) і утворюють з площиною ОXY кут
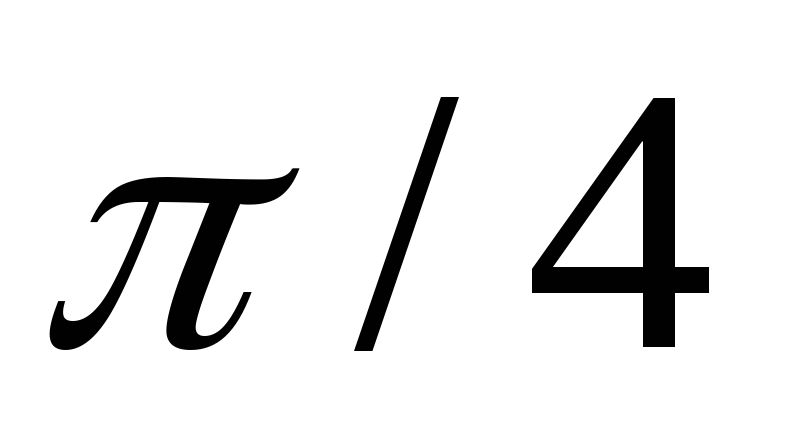 .
. -
Скласти рівняння поверхні, утвореної обертанням еліпса
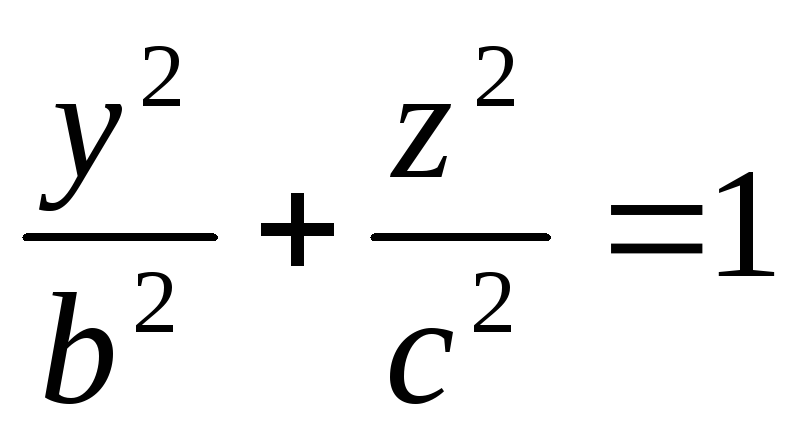 ,
x=0
навколо
осі
ОY.
,
x=0
навколо
осі
ОY. -
Скласти рівняння поверхні, утвореної обертанням еліпса
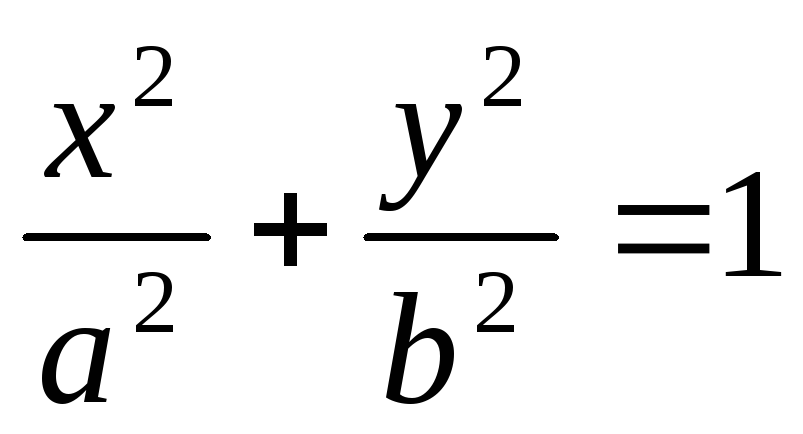 ,z
= 0 навколо
осі
ОX.
,z
= 0 навколо
осі
ОX. -
Скласти рівняння поверхні, утвореної обертанням гіперболи
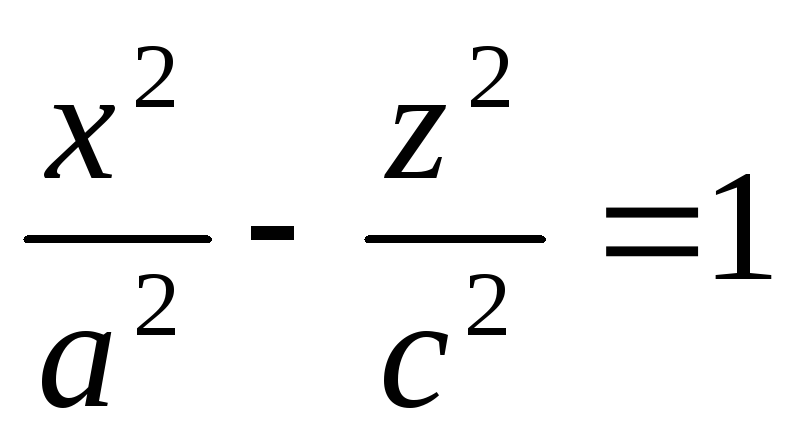 ,
y=0
навколо
осі ОZ.
,
y=0
навколо
осі ОZ. -
Пряма х=1, у=0 обертається навколо осі ОZ. Скласти рівняння утвореної поверхні обертання.
