
- •1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы.
- •3. Классическое, статистическое, геометрическое определение вероятности.
- •4. Аксиоматическое определение вероятности (по Колмогорову). Свойства вероятности. Свойства вероятности для полной группы событий.
- •5. Условная вероятность и её свойства. Независимость событий. Основные формулы вычисления вероятностей: формула умножения вероятностей, формула сложения вероятностей.
- •6. Формула полной вероятности. Формула Байеса.
- •9. Характеристическая функция и ее свойства.
- •10. Мода и медиана. Квантиль
- •11. Основные дискретные распределения. Вырожденное распределение. Испытания Бернулли. Биноминальное распределение. Распределение Пуассона. Теорема Пуассона.
- •12. Основные непрерывные распределения. Равномерное распределение. Экспоненциальное распределение. Нормальное распределение. Логарифмически нормальное распределение.
- •18. Основные распределения в статистике. Распределение хи-квадрат. Распределение Стьюдента. Распределение Фишера.
- •19. Статистические оценки. Точечные оценки. Метод максимального правдоподобия. Метод наименьших квадратов. Интервальные оценки.
1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы.
Частотой
события нзв отношение числа испытаний,
в которых событие произошло, к числу
всех произведенных испытаний.![]()
Числовая хар-ка
сл.события, обладающая тем свойством,
что для любой достаточно большой серии
испытаний частота события лишь
незначительно отличается от этой хар-ки,
нзв вероятностью
события.
![]()
Р![]() азмещениями
из n
элементов по m
в каждом
азмещениями
из n
элементов по m
в каждом
![]() или
или
При размещении с
повторениями:
![]()
Перестановками из n элементов
![]() С повторениями:
С повторениями:
![]()
Сочетаниями
из n элементов по m
![]()
С повторениями:
![]()
2. Математическая формализация случайного эксперимента. Пространство элементарных событий. Классификация событий. Операции над событиями и свойства операций.
Случайным нзв событие, к-рое может произойти или не произойти в рез-те некотор. испыт.
Испытание (опыт, эксперимент) — это процесс, включ. опред. усл-я и приводящий к одному из неск. возм. исходов. Исходом опыта м.б. рез-тат наблюдения или измерения.
Возможные исходы wi эксперимента G нзв элементарными событиями, если они явл.взаимоисключ.и в рез-те опыта одно из них обязательно происх.
Случайное событие может состоять из нескольких элементарных событий, подразделяющихся на достоверные, невозможные, совместные, несовместные, единственно возможные, равновозможные, противоположные.
Событие, которое обязательно произойдет в результате испытания, нзв достоверным
Событие, которое не может произойти в результате данного опыта (испытания), нзв невозможным.
Неск-ко событий нзв несовместными в данном опыте, если появление одного из них исключает появление других.
Неск-ко событий нзв совместными, если в рез-те эксперимента наступление одного из них не исключает появления других.
События нзв единственно возможными, если в рез-те испытания хотя бы одно из них обязательно произойдет.
Сов-ть всех единственно возможных и несовместных событий нзв полной группой событий.
Два ед. возм. и несовмест. соб. нзв противоположными.
События нзв равновозможными, если в рез-те испытания по условию симметрии ни одно из них не явл.объективно более возможным, чем другие.
Сов-ть Ω всех элемент.событий wi в опыте G нзв пространством элемент.событий. Пространство элемент.событий – это математическая модель опыта, в к-рой любому событию ставится в соответствие некоторое подмнож-во пространства Ω.
![]()
Мн-во Ω м.б. конечным, счетным или несчетным.
Операции над событиями:
Соб. А1 и А2 нзв равными, если осуществление соб.А1 влечет за собой осуществление соб. А2 и наоборот.
А1=А2
Суммой (объединением) соб. А и B нзв соб.C, к-рое означает осущ-е хотя бы одного из соб. А или B.
![]()
Произведением (пересечением) соб. А и B нзв соб. C, к-рое означает, что одновременно осущ-ся и А и B.
![]()
Разностью соб. А и B нзв соб. C, к-рое означает, что происх. соб. А, но не происх. соб. B.
![]()
Соб. Ā нзв противоположным по отношению к соб. А, если оно состоит из элемент.соб., не входящих в соб.А, но входящих в простр-во элемент.соб. Ω.
![]()
Ā=Ω\А
А+Ā=Ω
Несовместные события:
![]()
А∙B=Ø
Свойства операций:
Ω+А=Ω
Ω∙А=А
А∙А=А
А+Ø=А
А∙Ø=Ø
(А\В)∙(В\А)=Ø
А+Ā=Ω
А∙Ā=Ø
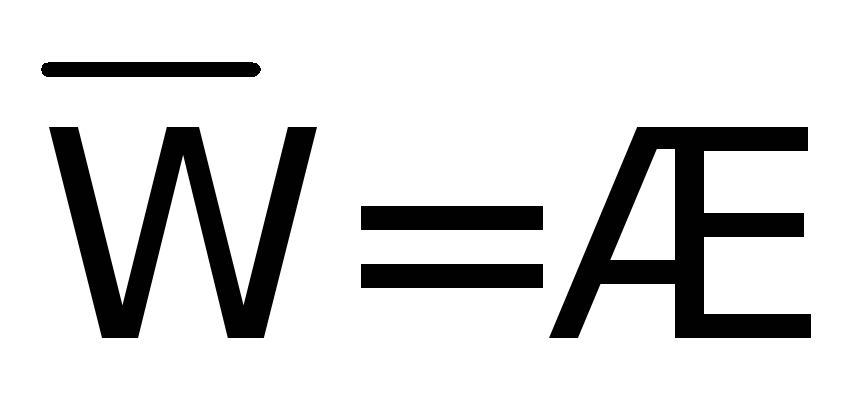
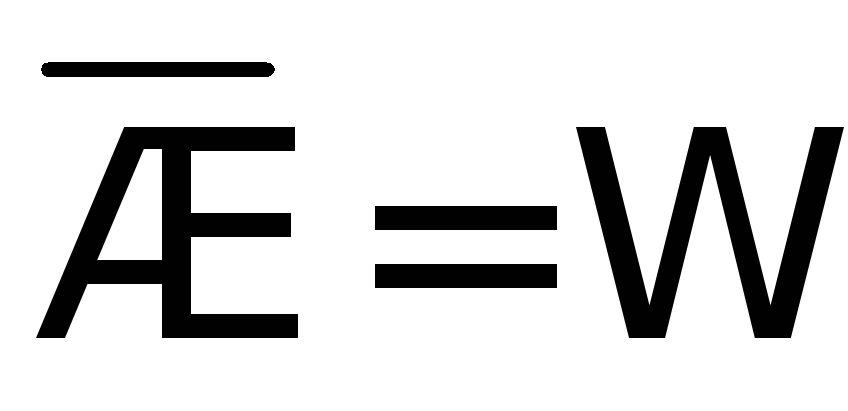
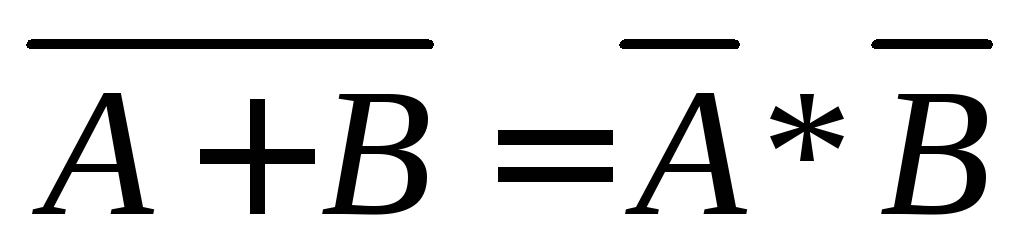
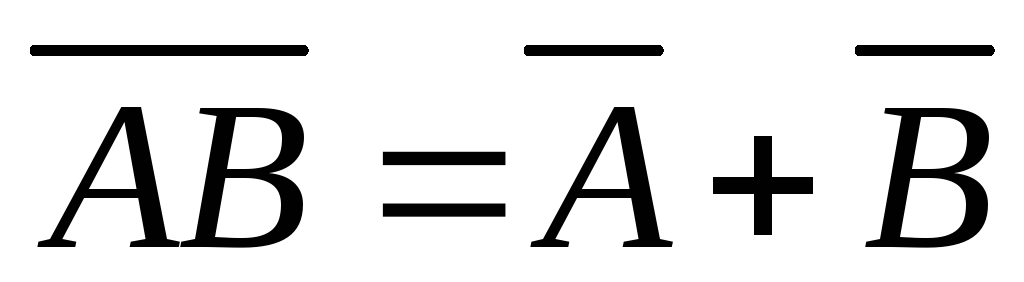
А+В=В+А
А∙В=В∙А
(А+В)+С=А+(В+С)
(А∙В)∙С=А∙(В∙С)
С(А+В)=СА+СВ
А+ВС=(А+В)(А+С)
