
Mathcad - ЛР4-2
.pdfМинистерство образования Российской Федерации Санкт - Петербургский государственный политехнический университет
Институт менеджмента и информационных технологий
Кафедра ПО ВТ и АС
Лабораторный практикум по курсу вычислительной математики
ОТЧЕТ
по лабораторной работе №4 (Часть II)
Тема:
АППРОКСИМАЦИЯ, ИНТЕРПОЛЯЦИЯ СПЛАЙНАМИ И ТРИГОНОМЕТРИЧЕСКИМИ МНОГОЧЛЕНАМИ
Выполнил: ______________
Группа: _____
Вариант: 14
Проверил: Царев В.А.
Отметка о зачете __________________
" ___ " ______________ 2006 г.
Череповец
2006
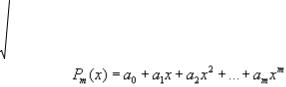
Задача 4_2.1. Функция y=f(x) задана таблицей значений y0, y1,...yn в точках x0, x1,...xn . Используя
метод наименьших квадратов (МНК), найти многочлен pm (x) = a0 + a1 x + ...+ am xm наилучшего
среднеквадратичного приближения оптимальной степени m=m* (среди возможных вариантов m =0,1,2,3). За оптимальное значение m* принять ту степень многочлена, начиная с которой величина остаточная
|
|
1 |
n |
|
дисперсия S(m) = |
|
× å(Pm (xi ) - yi )2 минимальна. |
||
(n +1) |
- (m +1) |
|||
|
i=0 |
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1.Считать векторы x и y исходных данных.
2.Используя функцию mnk (см. ПРИЛОЖЕНИЕ 4_2.В), найти многочлены Pm (x) , m=1,2,3 по методу
наименьших квадратов. Вычислить соответствующие им значения S(m) .
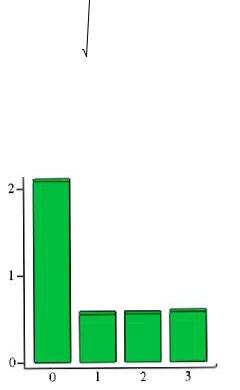
3. |
Построить гистограмму зависимости S(m) от m, на основании которой выбрать оптимальную степень |
m* многочлена наилучшего среднеквадратичного приближения. |
|
4. |
На одном чертеже построить графики многочленов Pm (x) , m=0,1,2,3 и точечный график исходной |
функции.
Теоретический материал:
Пусть функция y=f(x) задана таблицей своих значений: 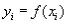 , i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого остаточная дисперсия
, i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого остаточная дисперсия
|
|
1 |
|
n |
|
|
s(a, m) := |
|
× å (P(a, m , xk) - yk)2 |
|
|||
(n + 1) - |
|
|
||||
|
|
(m + 1) |
минимальна. |
|||
|
|
|
|
k = 0 |
||
Так как многочлен |
определяется своими коэффициентами, |
|||||
то фактически нужно подобрать набор коэффициентов 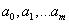 , минимизирующий
, минимизирующий
функцию 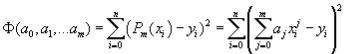 .
.
Используя необходимое условие экстремума, 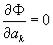 , k=0,1,-m получаем так называемую
, k=0,1,-m получаем так называемую
нормальную систему метода наименьших квадратов: 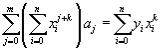 , k=0,1,-m.
, k=0,1,-m.
Полученная система есть система алгебраических уравнений относительно неизвестных
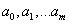 . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
. Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.

Исходные данные:
æ |
10 |
ö |
æ1.872 ö |
||
ç |
10.91 |
÷ |
ç |
2.204 |
÷ |
ç |
11.82 |
÷ |
ç |
2.564 |
÷ |
ç |
÷ |
ç |
÷ |
||
ç |
12.73 |
÷ |
ç |
2.950 |
÷ |
ç |
13.64 ÷ |
ç4.110 ÷ |
|||
ç |
14.55 |
÷ |
ç |
4.647 |
÷ |
x := ç |
15.45 |
÷ |
y := ç |
4.269 |
÷ |
ç |
÷ |
ç |
÷ |
||
ç |
16.36 ÷ |
ç5.820 ÷ |
|||
ç |
17.27 |
÷ |
ç |
5.282 |
÷ |
ç |
18.18 |
÷ |
ç |
7.123 |
÷ |
ç |
÷ |
ç |
÷ |
||
ç |
19.09 |
÷ |
ç |
6.402 |
÷ |
ç |
÷ |
ç |
÷ |
||
è |
20 |
ø |
è8.558 ø |
||
Решение задачи:
Функция mnk, строящая многочлен степени m по методу наименьших квадратов, возвращает вектор a коэффициентов многочлена:
mnk(x,y, n,m) := for j Î 0.. m
n
bj ¬ å yi × (xi)j i = 0
for kÎ 0.. m
n
Gj , k ¬ å (xi)k+j i = 0
a ¬ lsolve(G, b) a
Входные параметры:
x, y - векторы исходных данных; n+1 - размерность x,y.
m+1 - количество возвращаемых
коэффициентов
- формирование вектора правой части и матрицы нормальной системы Ga=b метода наименьших квадратов (базисные
функции - 1, x, , x2..., xm)
- встроенная функция MATHCAD,
решает систему линейных алгебраических уравнений Ga=b
Вычисление коэффициентов многочленов степени 0,1,2,3 по методу наименьших квадратов:
n := 11
a0 := mnk(x,y, n,0) a1 := mnk(x,y, n,1) a2 := mnk(x,y, n,2) a3 := mnk(x,y, n,3)
|
|
æ-4.56483312939456 |
ö |
|
æ-0.76 |
ö |
||
a0 = |
( 4.65008333333333 ) a1 = |
a2 = |
ç0.084 |
÷ |
||||
ç |
0.61432776418186 |
÷ |
||||||
|
|
è |
ø |
|
ç |
÷ |
||
|
|
|
|
|
|
è0.018 |
ø |
|
|
æ-13.558 |
ö |
||
|
ç |
2.788 |
÷ |
|
a3 = |
ç |
÷ |
||
ç |
-0.167 |
÷ |
||
|
||||
|
ç |
÷ |
||
|
è |
0.004 |
ø |
|
Функция P возвращает значение многочлена степени m в |
m |
точке t; многочлен задается с помощью вектора коэффициентов a: |
P(a,m,t) := å aj × tj |
|
j = 0 |
Функция s0 возвращает значение среднеквадратичного уклонения многочлена P(a,m,t) в заданных узлах:
|
|
|
|
|
|
|
|
1 |
|
|
n |
2 |
|
s0(a,m) := |
|
× |
å (P(a,m,xk) - yk) |
|||
(n + 1) - (m + 1) |
|
|
||||
|
|
|
|
k = 0 |
|
|
Вычисление значений sm, m=0,1,2,3: |
|
|
||||
s0 := s0(a0,0) |
s1 := s0(a1,1) |
|
s2 := s0(a2,2) |
|
s3 := s0(a3,3) |
|
æ 2.08030563568885 ö ç0.551090611989194 ÷
s = ç0.552952169716338 ÷
ç ÷
è0.574594334573263 ø
min(s) = 0.551090611989194
s1 = 0.551090611989194
s
Оптимальная степень m*=1; многочлен наилучшего среднеквадратичного приближения:
P12(x) := -4.564 + 0.614 × x |
a1 = |
æ-4.565 |
ö |
|
è 0.614 |
ø |
|||
|
|
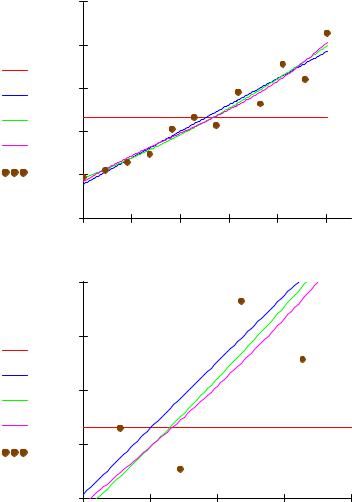
Графики многочленов степени 0,1,2 и точечный график исходной функции: |
|||||||
t := x0, x0 + 0.05.. xn |
i := 0.. n |
|
|
|
|
||
|
10 |
|
|
|
|
|
|
P(a0, 0, t) |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(a1, 1, t) |
6 |
|
|
|
|
|
|
P(a2, 2, t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(a3, 3, t) |
4 |
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t , t , t , t , xi |
|
|
|
6 |
|
|
|
|
|
|
P(a0, 0, t) 5.5 |
|
|
|
|
|
|
|
P(a1, 1, t) |
|
|
|
|
|
|
|
P(a2, 2, t) |
5 |
|
|
|
|
|
|
P(a3, 3, t) |
|
|
|
|
|
|
|
yi |
4.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
14 |
15 |
|
16 |
17 |
18 |
|
|
|
|
|
t , t , t , t , xi |
|
|
Вывод: Наиболее оптимальным приближающим многочленом в данном случае оказался |
|||||||
многочлен степени 1. Это означает, что дискретно заданная функция на |
|||||||
представленном отрезке оси абсцисс с наибольшей вероятностью представляет |
|||||||
линейную зависимость. |
|
|
|||||

Задача 4_2.2. Зависимость между величинами x и y описывается функцией y=f(x, a, b), где a и b –
неизвестные параметры. Найти эти параметры по табличным данным, сведя исходную задачу к линейной задаче метода наименьших квадратов.
Теоретический материал:
При эмпирическом (экспериментальном) изучении функциональной зависимости
одной величины у от другой х производят ряд измерений величины у при различных значениях величины х. Полученные результаты можно представить в виде таблицы, графика:
X |
x1 |
x2 |
… |
xn |
|
|
|
|
|
Y |
y1 |
y2 |
… |
yn |
|
|
|
|
|
|
|
|
|
|
Задача заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе функции, описывающей результаты эксперимента. Свести исходную задачу к линейной задаче МНК можно, сделав подходящую замену переменных. Например, если исходная зависимость имеет вид
y =
 a+bx+2, то преобразовав данное равенство к виду (y-2)2 =a+bx
a+bx+2, то преобразовав данное равенство к виду (y-2)2 =a+bx
Þy2 -4y+4=a+bx |
|
и введя новую переменную m= y2 -4y+4, получаем |
|||||
задачу об определении коэффициентов линейной зависимости m=а+bx. |
|||||||
Исходные данные: |
|
|
|
||||
æ 1 |
ö |
æ |
3.178 |
ö |
|||
ç |
1.9 |
÷ |
ç |
3.269 |
|
÷ |
|
ç |
2.8 |
÷ |
ç |
3.492 |
|
÷ |
|
ç |
÷ |
ç |
|
÷ |
|||
ç |
3.7 |
÷ |
ç |
3.881 |
|
÷ |
|
ç |
4.6 |
÷ |
ç |
4.442 |
|
÷ |
|
ç |
÷ |
ç |
|
÷ |
|||
x := ç5.5 ÷ |
y := ç |
5.161 |
÷ |
||||
ç |
6.4 |
÷ |
ç |
6.018 |
|
÷ |
|
ç |
7.3 |
÷ |
ç |
6.993 |
|
÷ |
|
ç |
÷ |
ç |
|
÷ |
|||
ç8.2 ÷ |
ç |
8.071 |
÷ |
||||
ç |
9.1 |
÷ |
ç |
9.239 |
|
÷ |
|
ç |
|
|
÷ |
ç |
|
|
÷ |
è |
10 ø |
è10.488 |
|
ø |
|||
Решение задачи: |
|
|
|
||||
y = |
|
|
|
n := 10 |
|
||
|
a + bx3 |
|
|
||||
Для линеаризации данной зависимости необходимо произвести две замены переменных - т.к. мы видим, что не только функция являеться нелинейной, но и аргумент также нелинеен.
Замена переменных: t=y^2, x2=x^3
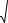
i := 0.. n
ti := (yi)2 |
x2i := (xi)3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
10.099684 |
|
|
0 |
|
1 |
|
|
|
1 |
|
10.686361 |
|
|
1 |
|
6.859 |
|
|
|
2 |
|
12.194064 |
|
|
2 |
|
21.952 |
|
|
|
3 |
|
15.062161 |
|
|
3 |
|
50.653 |
|
|
t = |
4 |
|
19.731364 |
|
x2 = |
4 |
|
97.336 |
|
|
5 |
|
26.635921 |
|
5 |
|
166.375 |
|
|||
|
|
|
|
|
|
|||||
|
6 |
|
36.216324 |
|
|
6 |
|
262.144 |
|
|
|
7 |
|
48.902049 |
|
|
7 |
|
389.017 |
|
|
|
8 |
|
65.141041 |
|
|
8 |
|
551.368 |
|
|
|
9 |
|
85.359121 |
|
|
9 |
|
753.571 |
|
|
|
10 |
|
109.998144 |
|
|
10 |
|
1·10 3 |
|
|
a1 := mnk(x2,t,n, 1) |
æ |
9.99926389145394 ö |
||||||||
a1 = ç |
÷ |
|||||||||
|
|
|
|
|
|
è |
0.100002069886299 ø |
|||
a := a10 |
b := a11 |
|
|
|
|
|
||||
|
|
|
|
Функция, полученная с использованием линеаризации |
||||||
Y(x) := |
a + b × x3 |
|
||||||||
Произведем проверку правильности приближения:
Vi := yi - (Y(x)i)
æ 1 ö
çç1.9 ÷÷ ç2.8 ÷
çç3.7 ÷÷
ç4.6 ÷ x := ç5.5 ÷
çç6.4 ÷÷
ç7.3 ÷ ç8.2 ÷
çç9.1 ÷÷ è 10 ø
æ |
3.178 |
ö |
|
|
0 |
|
ç |
3.269 |
÷ |
|
0 |
6.57713948446492·10 -5 |
|
ç |
÷ |
|
1 |
1.80933608580514·10 -4 |
||
3.492 |
|
|||||
ç |
÷ |
|
|
|
||
|
2 |
-6.37636787201856·10 -5 |
||||
ç |
3.881 |
÷ |
|
|||
|
3 |
-3.23065322528571·10 -4 |
||||
ç |
4.442 |
÷ |
|
|||
ç |
÷ |
V = |
4 |
-1.91504866351444·10 -4 |
||
y := ç |
5.161 |
÷ |
5 |
-1.15021852061581·10 -4 |
||
|
||||||
ç |
6.018 |
÷ |
|
|
|
|
|
6 |
1.75933135962758·10 -4 |
||||
ç |
6.993 |
÷ |
|
|
|
|
|
7 |
2.00120111557567·10 -5 |
||||
ç |
÷ |
|
||||
ç |
8.071 |
÷ |
|
8 |
2.37634490590111·10 -4 |
|
ç |
9.239 |
÷ |
|
9 |
6.47963229862825·10 -5 |
|
ç |
÷ |
|
|
|
||
|
10 |
-1.52066868277956·10 -4 |
||||
è10.488 ø |
|
|||||
|
|
|
||||
Вывод: Как видно из результатов проверки, функция, полученная с использованием линеаризации, достаточно точно отражает таблично представленную зависимость, причем на всей представленной области определения.
Задача 4_2.3. Функция y=f(x) задана таблицей значений y1 , y2 ,...yn в точках x1 , x2 ,...xn . Построить
кубический сплайн по заданным узлам и с его помощью восстановить пропущенное значение функции. На один чертеж вывести график сплайна и точечный график функции.
Теоретический материал:
В алгебраическом интерполировании при увеличении числа узлов увеличивается, как правило, степень интерполяционного многочлена. Кроме того, когда интерполирование выполняется для функций, не являющихся достаточно гладкими, интерполирование высокого порядка нецелесообразно. В этих случаях лучший результат может дать сплайн- интерполирование.
Пусть функция f (x) определена на отрезке [a,b] и известны ее значения в системе узлов a = x1 < x2 < ... < xn = b . Назовем функцию Sm (x) интерполяционным сплайном порядка m для функции f (x) , если выполнены следующие условия:
1) на каждом из отрезков [xk −1, xk ] (k=2,…,n) Sm (x) является многочленом степени m;
2)на всем отрезке [a,b] Sm (x) имеет непрерывные производные до порядка m-1;
3)Sm (xk ) = f (xk ) (k=1,…,n).
Если |
m ³ 2 , |
то |
для |
единственности Sm (x) следует задать дополнительно еще m-1 |
||||||||||||||||||
условий, которые обычно задаются на концах отрезка [a,b] либо произвольно, либо из |
||||||||||||||||||||||
дополнительной информации о поведении |
f (x) . |
|
|
|
|
|
|
|||||||||||||||
При |
m=1 |
получаем |
известный |
метод ломаных. Очевидно, что S1 (x) равномерно |
||||||||||||||||||
сходится к непрерывной на |
[a,b] |
функции |
|
f (x) , если |
max |
|
xi - xi−1 |
|
® 0 при n ® ¥ . |
|||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2≤k≤n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 (x) и кубического |
||||
Равномерная сходимость имеет место для квадратичного сплайна |
||||||||||||||||||||||
сплайна |
S3 (x) , причем скорость сходимости повышается вместе порядком сплайна и |
|||||||||||||||||||||
гладкостью |
|
f (x) . Этими замечательными свойствами сплайн - интерполирования отчасти |
||||||||||||||||||||
объясняется его широкое применение в различных задачах численного анализа. |
||||||||||||||||||||||
Рассмотрим построение кубического сплайна S3 (x) . |
Пусть на отрезке [a,b] заданы |
|||||||||||||||||||||
значения функции |
f (x) |
в узлах xi |
(i=1,…,n), |
x1 = a , xn = b . По определению S3 (x) на i- |
||||||||||||||||||
ом отрезке [xi , xi+1 ] |
является кубическим многочленом. Обозначим его Pi (x) . Будем Pi (x) |
|||||||||||||||||||||
искать по формуле |
|
|
|
|
|
)2 |
|
|
|
|
)3 , i=1,…, n-1. |
|
|
|
||||||||
P (x) = a |
i |
+ b (x - x |
) + c |
(x - x |
+ d |
i |
(x - x |
(1) |
||||||||||||||
i |
|
|
i |
i |
|
i |
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
||
По определению S3 (x) должны выполняться условия: |
|
|
|
|
|
|
||||||||||||||||
Pi (xi ) = f (xi ) , i=1,…, n-1, |
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||
Pi (xi+1 ) = f (xi+1 ) , i=1,…, n-1, |
|
|
|
|
|
|
|
|
|
|
(3) |
|||||||||||
¢ |
|
|
¢ |
(xi+1 ) , i=1,…, n-2, |
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||
Pi (xi+1 ) = Pi+1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
¢¢ |
|
|
¢¢ |
(xi+1 ) , i=1,…, n-2. |
|
|
|
|
|
|
|
|
|
|
(5) |
|||||||
Pi (xi+1 ) = Pi+1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Дополнительные условия рассмотрим в виде: |
|
|
|
|
|
|
||||||||||||||||
¢¢ |
|
|
|
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
||
P1 (x1 ) = 0, Pn−1 (xn ) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Примечание. Сплайн с такими дополнительными условиями называется естественным. Возможны и другие способы выбора дополнительных условий.
|
Введем обозначения: |
|
||||||
h |
= x |
i+1 |
- x |
, g |
i |
= |
f (xi+1 ) - f (xi ) |
, i=1,…, n-1. |
|
||||||||
i |
|
i |
|
|
hi |
|
||
|
|
|
|
|
|
|
|
|
Подставляя в (2)-(6) формулу (1) и используя (7), получаем соответственно следующие
соотношения: |
|
|
|
|
|
|
|
|
|
|
||||||
ai = f (xi ) , i=1,…, n-1, |
(8) |
|||||||||||||||
b + c |
h + d |
h2 |
= b |
, i=1,…, n-1, |
(9) |
|||||||||||
i |
|
i |
|
i |
|
i i |
|
h2 |
i+1 |
|
|
|
|
|
||
b + 2c h + 3d |
i |
= b |
+1 |
, i=1,…, n-2, |
(10) |
|||||||||||
i |
|
|
i |
i |
|
|
|
i |
|
i |
|
|
||||
di |
= |
ci+1 - ci |
, i=1,…, n-1, |
(11) |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
3hi |
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
= 0 , cn |
= 0 . |
|
|
|
|
|
|
(12) |
|||||||
Подставив (11) в (9), получим формулу |
|
|||||||||||||||
b |
= g |
|
- |
1 |
h (c |
i+1 |
+ 2c |
) , i=1,…, n-1. |
(13) |
|||||||
|
|
|||||||||||||||
i |
|
|
i |
3 |
|
i |
|
|
|
i |
|
|
|
|||
Используя (11) и (13), из (10) получаем уравнение |
|
|||||||||||||||
hi ci + 2(hi |
+ hi+1 )ci+1 + hi+1ci+2 = 3(gi+1 - gi ) , i=1,…, n-2. |
(14) |
||||||||||||||
Добавив уравнения (12), окончательно получим систему линейных алгебраических уравнений относительно неизвестных c1,c2 ,...,cn с трехдиагональной матрицей. После
решения этой системы и определения c1,c2 ,...,cn по формулам (8), (11) и (13) находятся все остальные коэффициенты.
Исходные данные:
n := 6
æ−21 |
ö |
æ −9 |
ö |
||
ç |
−11 |
÷ |
ç |
−15 |
÷ |
ç |
÷ |
ç |
÷ |
||
ç |
−7 ÷ |
ç |
−27 ÷ |
||
x := ç |
1 |
÷ |
y := ç |
−27 |
÷ |
ç |
8 |
÷ |
ç |
−28 |
÷ |
ç |
÷ |
ç |
÷ |
||
ç |
9 |
÷ |
ç |
−14 |
÷ |
ç |
12 |
÷ |
ç |
|
÷ |
è |
ø |
è−15 |
ø |
||
Решение задачи:
Найдем коэффициенты g и h:
g(x,y, n,h) := |
|
for |
i 0.. n − 1 |
h(x,n) := |
|
|
|
for i 0.. n − 1 |
|
|
|
|
|||||||
|
|
g ← |
yi+1 − yi |
|
|
|
|
hi ← xi+1 − xi |
|
h |
|
|
|
|
h |
||||
|
|
i |
|
|
|
|
|
||
|
|
g |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
g := g(x,y, n,h) |
|
|
h := |
h(x,n) |
|||||
|
|
|
|
|
|
|
|||
a := y

|
æ |
-0.6 |
ö |
|
æ10 ö |
|||
|
ç |
-3 |
÷ |
|
ç |
4 |
÷ |
|
|
ç |
0 |
÷ |
|
ç |
8 |
÷ |
|
g = |
ç |
÷ |
h = |
ç |
÷ |
|||
ç |
-0.142857142857143 |
÷ |
ç |
7 |
÷ |
|||
|
|
|||||||
|
ç |
÷ |
|
ç |
÷ |
|||
|
ç |
14 |
÷ |
|
ç |
1 |
÷ |
|
|
è-0.333333333333333 ø |
|
è 3 ø |
|||||
Зададим вектор - столбец свободных членов:
b(n,g) := |
|
|
for i Î 0.. n - 2 |
|
|
|
|
|
|||
|
|
|
bi ¬ 3 × (gi+1 - gi) |
|
|
|
|
|
b |
|
|
B := b(n, g) |
æ |
-7.2 |
ö |
||
|
|
|
ç |
9 |
÷ |
|
|
|
ç |
÷ |
|
|
|
|
|
||
B= ç-0.428571428571429 ÷ çç 42.4285714285714 ÷÷
è -43 ø
Зададим главную и побочные диагонали в виде 3 массивов:
d0(n,x) := |
|
for i Î 0.. n - 2 |
d1(n,x) := |
|
|
|
for i Î 0.. n - 2 |
d2(n,x) := |
|
|
|
for i Î 0.. n - 3 |
|
|
|
|
|
||||||||
|
|
di ¬ hi |
|
|
|
|
di ¬ 2 × (hi + hi+1) |
|
|
|
|
di ¬ hi+1 |
|
|
d |
|
|
|
|
d |
|
|
|
|
d |
d0 := d0(n,x) |
d1 := d1(n,x) |
d2 := d2(n,x) |
||||||||||
Сформируем из выше заданных массивов трехдиагональную матрицу:
A(d0, d1, d2,n) := for i Î 0.. n - 2 Ai , i ¬ d1i
for i Î 0.. n - 3 Ai+1, i ¬ d0i Ai , i+1 ¬ d2i
A
A := A(d0, d1,d2, n)
æ28 |
4 |
0 |
0 |
0 ö |
||
ç |
10 |
24 |
8 |
0 |
0 |
÷ |
ç |
÷ |
|||||
A = ç 0 |
4 |
30 |
7 |
0 ÷ |
||
ç |
0 |
0 |
8 |
16 |
1 |
÷ |
ç |
|
|
|
|
|
÷ |
è 0 |
0 |
0 |
7 |
8 ø |
||
