Учебные пособия и методические указания / Определенный интеграл

Добавил:

Mary Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный строительный университет

Предмет:

Высшая математика

Файл:

ного плоскостями x = 0;

z = 0; y = 1,

y = 3, x + 2z = 3 (рис. 4.7)

.pdf

Скачиваний:

Добавлен:

04.01.2014

Размер:

573.19 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

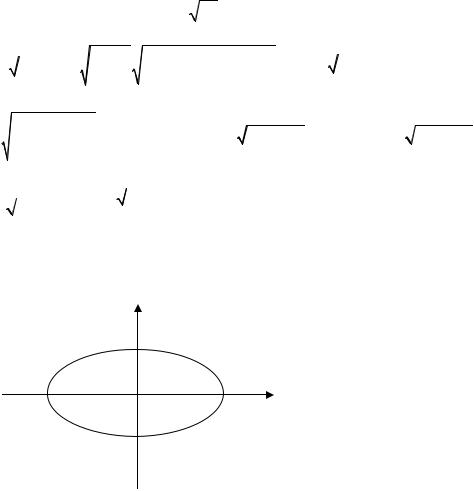
4. Приложения определенного в механике.

Интеграл по фигуре применяется при вычислении массы, статических моментов и моментов инерции фигур, при нахождении положения центра тяжести.

4.1 Определение массы фигуры

Известно, что масса любой фигуры может быть определена, если известна длина, площадь или объем фигуры и плотность в каждой т. фигуры так, если фигура-

																																											b											(1)
отрезок, то масса M его определяется формулой M = ∫ ρdx ,																																																						(1)
где ρ ( x) – плотность.																																											a
где ρ ( x) – плотность.
Плоская линия Γ -															M = ∫ ρdL																																							(2)
																				Γ																																		(3)
Пространственная линия Γ - M = ∫ ρdL																																																						(3)
																											Γ
Плоская область S - M = ∫∫ ρ ( x, y) dS																																																						(4)
																						S						M = ∫∫ ρ ( x, y, z )dq																										(5)
Пространственная поверхность Q -																												M = ∫∫ ρ ( x, y, z )dq																										(5)
																														Q
Пространственное тело R -																							M = ∫∫∫ ρ ( x, y, z ) dV																															(6)
																										R
4.1 Найти массу M															дуги кривой x = t, y =																	1		t2 , z =				1	t3 (0 ≤ t ≤ 1) , линейная плотность
4.1 Найти массу M															дуги кривой x = t, y =																			t2 , z =					t3 (0 ≤ t ≤ 1) , линейная плотность
																															2						3
которой меняется по закону ρ =
которой меняется по закону ρ =																										2 y .
Решение:
							1																														1
							1									1						(xt′ )2 + ( yt						′)2 + (zt					)′2 dt =				1
M = ∫													2				t 2																				∫t					1+ t 2 + t 4 dt =
				2 ydL = ∫
				2 ydL = ∫
		Γ					0							2																							0
		Γ					0																														0
																											2	1																											1


	1	1					1 2				3											1		1	t			+												3								1
																													2
					2													2											2		4				2										2						4		2
=		∫0	t			+		+						d t					+				=							t			+ t			+1	+					ln		t			+		+	t		+ t		+1		=
=			t			+		+						d t					+				=							t			+ t			+1	+					ln		t			+		+	t		+ t		+1		=
	2						2				4											2		2				2												8								2
																																																							0
																																																							0

	1								3			3		+ 2 3

=		3 3 −1					+			ln											.
=		3 3 −1					+			ln											.
	8						2							3
	8						2							3
4.2 Найти массу пластинки, ограниченной эллипсом																																										x2		+		y2		= 1, если плотность в каж-
4.2 Найти массу пластинки, ограниченной эллипсом																																												+				= 1, если плотность в каж-
																																									16						9
дой точке равна расстоянию от точки до оси OX . (рис. 4.1)
																		y
																			3
																							S												x
																			0									4							x
																			0									4

Рис.4.1

Решение:

Заметим, что в точках симметричных относительно оси OX , плоскость одина-

кова (ρ ( x, y ) = y ) , следовательно

M = 2∫∫ ydS ,

где S - часть пластинки, расположенная выше оси OX .


3	1−	x2								x2			3x3	4
						x2
4	16		4	3	1−		4
M = 2 ∫ dx	∫		ydy = ∫ dx y2	0	16		= 9 ∫	1	−		dx =	9x −		= 48 .

−4	0		−4				−4			16			16	−4

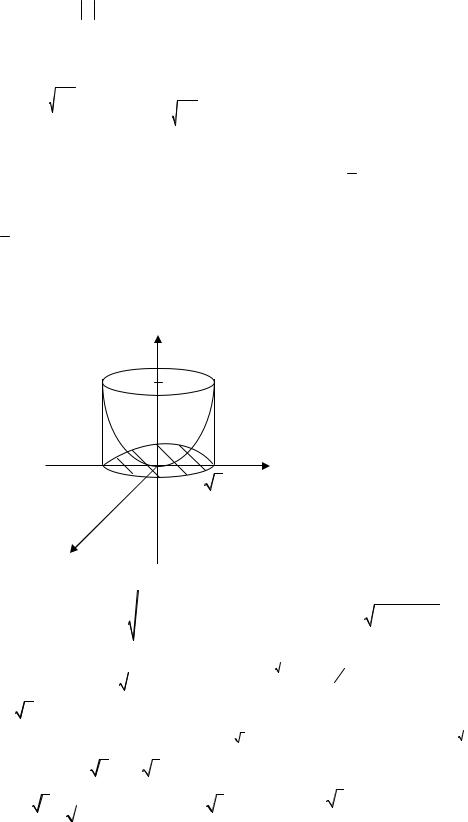
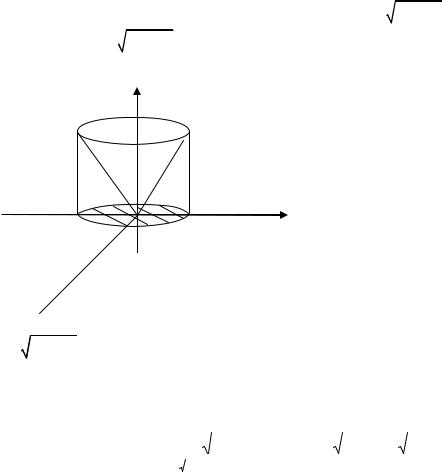
4.3 Найти массу оболочки, заданной уравнениями z = 12 (x2 + y2 ), 0 ≤ z ≤ 1 , если плот-

ность в каждой точке ρ = z .

z = 12 (x2 + y2 ) - параболоид вращения с осью вращения OZ , ограниченный сверху

плоскостью z = 1 (рис. 4.2.).

Линия пересечения параболоида с плоскостью z = 1 - окружность x2 + y2 = 2 .

Следовательно проекция оболочки на плоскость XOY - круг x2 + y2 = 2 . z

Рис. 4.2

Решение:

M = ∫∫ ρdq = ∫∫ z ( x, y)

∂z 2

+ y

dxdy = ∫∫

1+ x

+ y

dxdy =

∂x

∂y

x = r cosϕ

2π

r =

(1+ r2 )12 r3dr =

y = r sin ϕ

∫∫ r 2

1+ r2

rdrdϕ =

∫ dϕ ∫

r =

r =0

r 2 +1 = t 2

;tdt = rdr

2π

t =

t (t

−1)tdt =

2π

∫ dϕ ∫

∫ dϕ

−

= 0;t1 = 0; r = 2;t2 = 3

t =1

)

2π

π 12

3 + 2

2π

9 3

1 12 3 + 2

∫

− 3 −

(

dϕ

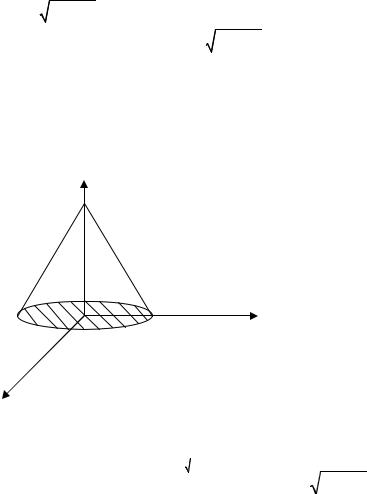
4.4 Найти массу тела, ограниченного поверхностями z = x2 + y2 , z = 1, если плот-

ность ρ ( x, y, z ) = x2 + y2 . (рис. 4.3)

0	S	1	x
0		1
1
		Рис. 4.3
Решение:

z = x2 + y2 - конус.

Линия пересечения конуса с плоскостью z = 1, есть круг x2 + y2 = 1, проекция конуса на плоскость XOY - S - x2 + y2 = 1.

M = ∫∫∫ρ(x, y, z)dV = ∫∫dS							1								dz = ∫∫(1 −				)			x = r cosϕ
																						x = r cosϕ

								∫				x 2	+ y 2					x 2 + y 2		x 2 + y 2	dS =	y = r sin ϕ	=
																						z = 1
	R			S			x		+ y							S						z = 1
	R			S			2				2					S
2π	1		2π										1			2π
					r	3				r		4		1			π
						3						4
= ∫ dϕ∫ (1 − r )r		2						−					=			∫ dϕ =
																	.
			dr = ∫ dϕ		3						4						.
0	0		0		3						4		0 12			0	6
0	0		0										0 12			0

4.2 Определение статических моментов, моментов инерции и центра тяжести.

Если фигура однородна (плотность ρ = const ) и имеет ось или плоскость симметрии, то статический момент относительно этой оси или плоскости равны нулю.

Если же имеется центр симметрии, то статический момент относительно любой оси, проходящий через центр, равен нулю.

При наличии у однородной фигуры плоскости, оси или центра симметрии, центр тяжести лежит на этой плоскости, оси или в центре симметрии. (Таблица).

Отрезок	Плоская	Плоская	ПространПространПростран-
[a, b] на	линия Γ	область	ственная	ственная	ственное
оси OX		S	линия Γ	поверх-	тело R
				ность Q

Статический

M x

= 0

M x

= ∫ yρ

M x

= ∫∫ yρ

M xy

= ∫ zρd

M xy

= ∫∫ zρd

M xy

= ∫∫∫zρd

момент отно-

сительно:

M y

= ∫ x

M y

= ∫ xρ

M y

= ∫∫ xρ

M xz

= ∫ yρd

M xz

= ∫∫ yρd

M xz

= ∫∫∫ yρd

осей

OX , OY : M x , M

M yz =

∫

xρd

M yz

= ∫∫ xρd

M yz =

∫∫∫

xρd

плоскостей

XOZ ,YOZ; XOY

Координаты

X C

M y

X C

M y

M x

X C =

M yz

M xz

M xy

X C ,YC , ZC ,

центра тяже-

сти

Момент инер-

= ∫ (x

= ∫∫(x

= ∫

+ y

= ∫∫

= ∫∫∫

ции относи-

Y0 = ∫ x ρ

тельно

Начала коор-

= ∫ y

= ∫∫ y

= ∫

= ∫∫

= ∫∫∫(y

динат:

Y0 - полярный

= ∫ x 2 ρ Yy

= ∫∫ x 2 ρ

Yy = ∫ (x2

= ∫∫(x 2 +

Yy = ∫∫∫(x2

момент

Осей коорди-

= ∫

= ∫∫

= ∫∫∫

нат

OX , OY , OZ

Yx ,Yy ,Yz

Yxy

= ∫ z 2 ρd

Yxy

= ∫∫ z 2 ρd Yxy

= ∫∫∫ z 2 ρd

Координат-

Yxz

= ∫ y

ρd

Yxz

= ∫∫ y

ρd

Yxz

= ∫∫∫ y

ρd

ных плоско-

стей

XOY , XOZ ,YOZ

Yxy ,Yxz ,Yyz

Yyz

= ∫ x 2 ρd

Yyz

= ∫∫ x 2 ρd Yyz

= ∫∫∫ x 2 ρd

4.5 Найти массу, статический момент относительно оси OX , а также координаты центра тяжести для пластины, ограниченной линиями y 2 = x , x = 2 , если плотность

ρ = y . (рис. 4.4)

y2 = x

	x
0	2
	S

Рис. 4.4

Решение:

Фигура симметрична относительно оси OX .

Значения плотности также симметричны относительно оси OX .

														2					y =		x		2				y	2			x			2
														2					y =		x		2					2			x			2
M = ∫∫ ρdS = ∫∫ ydS = 2∫ dx																			∫ ydy = 2∫ dx													= 2∫ xdx = 2
M = ∫∫ ρdS = ∫∫ ydS = 2∫ dx																			∫ ydy = 2∫ dx													= 2∫ xdx = 2
			S				S							0					0				0		2					0				0
			S				S			2				0					0		2		0							0	2			0

																x
																x
M y		= ∫∫ xρdS = 2∫ xdx ∫ ydy = ∫ dx(x y 2 )																								0 x			= ∫ x 2 dx =						8
																																			8

				S						0				0							0										0			3
				S						0				0							0										0

										2											2		y 4				x					2
					2					2					x		3				2		y 4				x				1	2	2			4
Yx = ∫∫ y						ρdS = 2∫ dx ∫ y												dy = 2∫ dx											=			∫ x		dx =

			S							0				0							0		4			0					2 0					3
			S							0				0							0		4			0					2 0
X		=		M y		=	8	=		4		;		Y = 0 , так как ось OX - ось симметрии

	C						3 2
	C			M						3					C
				M						3												C			.
Ответ: M = 2; M											=		8	; Y =					4	;			4	, 0
Ответ: M = 2; M									y		=			; Y =						;				, 0
									y	3							x		3				3
										3									3				3

4.6 Вычислить массу, статический момент относительно оси OX и момент инерции относительно OY пластины, определить координаты центра тяжести, пластина ограничена линиями y = x 2 , y = 1, если плотность ρ(x, y) = 2 y . (рис. 4.5)

-1

Рис. 4.5

Решение:

							1	1					1							1	(1− x4 )dx = 1, 6
M ∫∫ ρ ( x, y ) dS = ∫ dx ∫ 2 ydy = ∫ dxy2																	x =			∫	(1− x4 )dx = 1, 6
																	1
	S						−1	x2					−1					1		−1						2					1
	S						−1	x2					−1							−1
							1	1			2		1			y3					2		1	6				1		7			8
							1	1			2		1			y3					2		1	6				1		7			8
M x = ∫∫ yρdS = 2 ∫ dx ∫									y			dy = 2 ∫ dx								=			∫ (1− x		)dx =		x −		x			=
M x = ∫∫ yρdS = 2 ∫ dx ∫									y			dy = 2 ∫ dx				3				=	3		∫ (1− x		)dx =		x −	7	x			=	7
		S					−1	x2						−1		3		x2			3		−1			3		7			−1		7
		S					−1	x2						−1				x2					−1			3					−1
			1					1					1						x2				1
Yy = ∫∫ x2 ρdS = ∫ dx ∫ 2x2 ydy = ∫ dx x2 y2																			x2		= ∫ (x6 − x2 )dx = 4
																			1
		S			−1			x2					−1									−1				15
		S			−1			x2					−1									−1				15
Y =		M x	=	5	; X		= 0 (ось OY - ось симметрии)
Y =			=		; X	C	= 0 (ось OY - ось симметрии)
C		M	7			C
		M	7																	5
Ответ: M = 1, 6;						M x =			8	;		Yy =	4		;					5
																C	0,				.
									7				15			C	0,				.
									7				15							7

4.7. Найти координаты центра тяжести конического тела, ограниченного поверхностя-


ми z = 1−		x2 + y2 , z = 0 и имеющего плотность ρ = 1.

Коническая			поверхность z = 1− x2 + y2 имеет	ось симметрии	OZ и вершину в
т. (0, 0,1) .
Положив	в		уравнении z = 0 , найдем линию ее	пересечения с	плоскостью	XOY :
x2 + y2 = 1. Таким образом, данное коническое тело проецируется на плоскость						XOY в

круг x2 + y2 ≤ 1. В силу симметрии относительно оси OZ его центр тяжести лежит на этой оси, т.е. xc = 0, yc = 0 . (рис. 4.6.)

Рис. 4.6

Решение:

x = r cosϕ

z =1− x2 − y2

M = ∫∫∫ ρdV = ∫∫∫ dV = ∫∫ dS

∫ dz = ∫∫ dS (1−

) =

y = r sin ϕ

x2 + y2

z =0

z = 1

2π

π ;

= ∫∫ (1− r)rdrdϕ = ∫ dϕ∫ (1− r)rdr = ∫ dϕ

−

∫ dϕ =

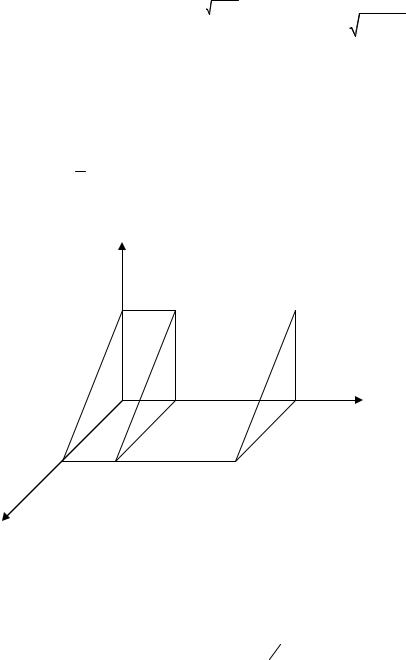
																	1−	x2 + y2								∫∫ dS (1−							)2			2π	1
			= ∫∫∫ zρdV = ∫∫∫ zdV = ∫∫ dS															∫							1									=	1	∫ dϕ∫(1− r 2 )rdr =
M xy																					zdz =				1					x2 + y2					1
M xy																					zdz =				2					x2 + y2					2
				R							R				S			6								S										0	0
	1	2π			1				2				3		1	2	1		2		2		3		1		4	1	1		1	2π				π
	1	2π			1				2				3		1	2	1		2		2		3		1		4	1	1		1	2π				π
=			∫ dϕ∫(z − 2r							+ r				)dr =		∫	(	r		−		r		+		r		dϕ =				∫ dϕ =
=	2		∫ dϕ∫(z − 2r							+ r				)dr =	2	∫	(	r		−	3	r		+	4	r		dϕ =				∫ dϕ =
	2		0		0										2	0	2				3				4			0	2 12			0		12
			0		0		π									0												0				0
x =				M xy	=		π	3	=		1	.
x =					=				=			.
c				M		12		π			4
				M		12		π			4

Ответ: C (0,0, 1 ). 4

4.8. Найти координаты центра тяжести ρ = 1 призматического тела ограничен-

	y = 1	y
0	y = 1	y2 = 3
0	1
3
A		D

x	Рис. 4.7

Решение:

Рассмотрим тело R ABY1CY2 D
	(3−x )

3 3

M ∫∫∫ ρdxdydz = ∫ dx∫ dy

2	3	3	3 − x	3
∫ dz = ∫ dx∫				dy = ∫ (3 − x)dx =	3x
∫ dz = ∫ dx∫			2	dy = ∫ (3 − x)dx =	3x
0	0	1	2	0

	1		2	3	9

−		x		=		.
	2				2
				0

				M yz														3		3			(3−x)					3	2						3
				M yz					2							2		3		3					2		2	3	2	3		1		2	3
X C	=						=				∫∫∫xρdxdydz =							∫ xdx∫ dy						∫ dz =				∫ x(3 − x)dx =			x −		x		= 1.
X C	=						=				∫∫∫xρdxdydz =					9		∫ xdx∫ dy						∫ dz =			9	∫ x(3 − x)dx =		2	x −		x		= 1.
				M 9							R					9		0		1							9	0	9	2		3			0
		M xz									R							0		1				3				0	9						0
								2		∫∫∫ yρdxdydz =					4					1		2
								2							4					1		2
Yc =						=												3x −			x				= 2.
Yc =			M			=		9							9			3x −		2	x				= 2.
			M					9			R				9					2				0
											R													0	3
			M xy					2		∫∫∫ zρdxdydz =						1			−(3 − x)2						3	1
ZC	=					=																			=		.
ZC	=			M		=		9												3					=	2	.
				M				9			R				18					3					0	2
											R				18										0
Ответ: X							= 1,				Y = 2,	Z		=	1		.
Ответ: X					C		= 1,				Y = 2,	Z	C	=			.
					C						C		C		2
															2

4.9 Найти массу и момент инерции относительно начала координат пластинки, ограниченной линиями x2 + y2 = x; x2 + y2 = 2x; ρ(x, y) = x . (Рис. 4.8)

0	1	2	x

	S

Рис. 4.8

Решение:

Перейдем к полярной системе координат x = r cosϕ, y = r sin ϕ

x 2

+ y 2 = x

r 2

= r cosϕ → r = cosϕ

x 2

+ y 2 = 2x

= 2 cosϕ

r 2

= 2r cosϕ → r

2 cos ϕ

M = ∫∫ ρdS = ∫∫ xdxdy = ∫ dϕ

∫ r 2 cosϕdr = ∫ dϕ

cosϕ

∫ cos4 ϕdϕ =

−

cos ϕ

−

cos ϕ

1 + cos 2ϕ

(1 + cos 2ϕ)

1 + cos 4ϕ

cos

ϕ =

∫

dϕ =

∫

+ 2 cos 2ϕ +

dϕ =

−

ϕ + sin 2ϕ +

sin 4ϕ

π.

−π

2 cosϕ

= ∫∫(x2 + y2 ) ρdS = ∫ dϕ

∫

r 4 cosϕ dz =

∫ cos6 ϕdϕ =

−

cosϕ

−

4.10 Найти полярный момент инерции круга x2 + y2 = 2ax ; ρ = 1. (рис 4.9) Преобразуем исходное уравнение:

x2 − 2ax + a2 + y2 = a2 ; (x − a)2 + y2 = a2

y
0	a	2a	x
	a	2a

Рис. 4.9

Решение:

В полярных координатах круг имеет вид

x2 + y2

= 2ax

→ r = 2a cosϕ

r 2

= 2ar cosϕ

Sr =2a cos ϕ

2a cos ϕ

I 0

= ∫∫(x 2

+ y 2 )ρdS = ∫ dϕ

∫ r 3 dr = ∫ dϕ

= 4a 2

∫ cos4 ϕdϕ =

−

(1+ cos 2ϕ2 )

1+ 2 cos 4ϕ

∫

dϕ

∫

1+ 2 cos 2ϕ +

dϕ

= a

ϕ + sin 2ϕ +

sin 4ϕ

−

−π

= a4

4.11 Найти центр тяжести однородной полуокружности x 2

+ y 2 = a 2 , располо-

женной над осью OX и имеющую плотность ρ = x . (рис. 4.10)

		x
0	a	x
	a

	Рис. 4.10
	Рис. 4.10

Решение:

Фигура является симметричной относительно оси OY , поэтому X C = 0 .

Найдем массу линии, представив ее уравнение в параметрическом виде

x = a cos t, y = a sin t , где пределы изменения параметра t

соответствуют значе-

ниям координаты x на концах линии:

x = a; cos t1 = 1 → t1 = 0;

x = −a; cos t2 = −1 → t2 = π.

M = ∫ ρdL = ∫

dL = ∫

a cos t

(xt′)2

+ ( yt′) 2

dt = a∫

cos t

a 2 sin 2 t + a 2 cos 2 t

dt = a 2 ∫

cos t

dt =

Рассмотрим график функции

cos t

при 0 ≤ t ≤ π .

f (t )

cos t


0	π	π
	2

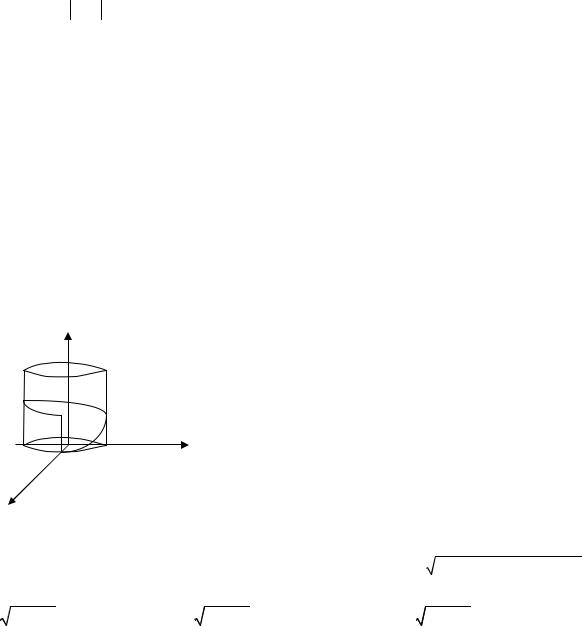
Он симметричен относительно линии t = π , следовательно:

							2
				π		π		π
	π			π		π		2
	π	2				2
=	∫		cos t	dt = 2∫ cos t dt		∫ cos tdt =2a2 sin t		= 2a2 .
								= 2a2 .

	0	0			0
								0
								0

При вычислении статического момента используем ранее предложенное относительно cos t .

cos

2 = a3 .

M x

= ∫ ρ ydL = ∫

ydL = a3 ∫

cos t

sin tdt = 2a3 ∫ cos t sin tdt = −2a3

M x

a 3

2a 2

Ответ: M = 2a2 ; M

= a3 ;

= 0; Y =

4.12 Найти момент инерции относительно плоскости XOY первого витка линии y = a sin t, x = a cos t, z = bt. (рис. 4.11), если плотность в каждой точке равна

ρ = x 2 + y 2 + z 2 .

Пределы изменения t найдем из условия, что в конце первого витка коор-

динаты x	и y принимают такие же значения, что и в начале витка: x = a;
a cos t = a;	cos t = 1. Значит t1 = 0, t2 = 2π .
	z

0	y
	y
a

x	Рис. 4.11

Решение:

2π

I xy = ∫ z2 ρdL = ∫ z2 (x2 + y2 + z2 )dL = ∫ b2t 2 (a2 cos2 t + a2 sin2 t + b2t 2 )a2 sin2 t + a2 cos2 t + b2 dt =

2π

(a2t2 + b2t 4 )dt = b2

2π

= b2

a2 + b2 ∫

a2 + b2

+ b2

= 8π 3b2 a2 + b2

π 2b2

4.13

Найти

координаты

центра тяжести

фигуры

ограниченной

линиями

y2 = 4x + 4;

y2 = −2x + 4;

ρ = 1. (рис. 4.12)

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в папке Учебные пособия и методические указания

#
04.01.2014631.81 Кб141Векторная алгебра и аналитическая геометрия.doc
#
04.01.2014564.74 Кб94Неопределённый интеграл.doc
#
04.01.2014573.19 Кб95Определенный интеграл.pdf
#
04.01.2014137.92 Кб63Ряды.pdf
#
04.01.20142.27 Mб137Теория вероятностей.doc
#
04.01.2014392.19 Кб91Теория пределов.doc
#
04.01.20141.18 Mб100Элементы линейной алгебры.doc