
Учебные пособия и методические указания / Определенный интеграл
.pdf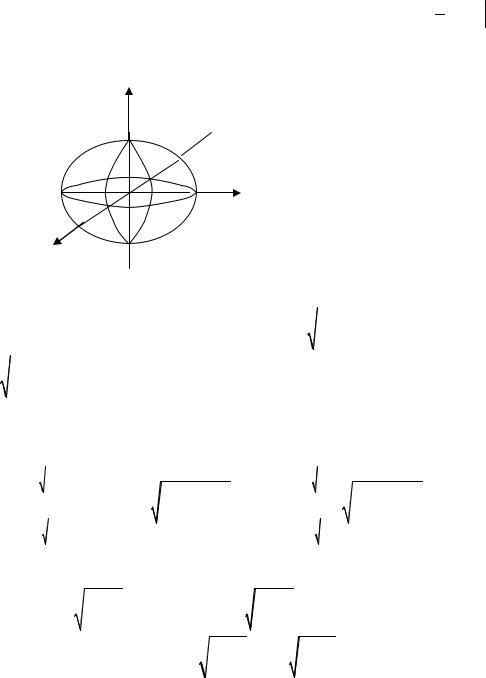
Решение:
Область S (проекция R на плоскость XOY ) - круг x2 + y2 ≤ 1 Поверхность входа z = 2 − x
Поверхность выхода z = 4 − 2x Следовательно, по (2.16)
|
|
4−2 x |
|||
V = ∫ ∫ ∫dV = ∫ ∫dS |
∫ |
dz = ∫ ∫dSz |
|
2−x |
|
|
|
|
|
|
4−2 x |
R |
S |
2−x |
S |
|
|
|
|||||
перейдем к полярным координатам
= ∫ ∫(2 − x)dS =
S
x = r cosϕ , y = r sin ϕ , r = 1 .
2π |
1 |
|
2π |
|
3 |
cosϕ) |
|
2π |
|
|
|
|
|
|
|
= ∫dϕ∫(2 − r cosϕ)rdr = ∫ (r 2 − r |
|
0 dϕ = ∫ (1− 1 cosϕ)dϕ |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
||||
0 |
0 |
0 |
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||
2.3.5. Вычислить объем эллипсоида (рис. 41) |
x2 |
+ |
y2 |
+ |
z2 |
= 1 . |
|||||||||
a2 |
b2 |
c2 |
|||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
y |
|
|
|
|
|
|
||
|
|
−b |
|
|
b |
|
|
|
|
|
|
||||
a
Рис. 41
x
= (ϕ − 1 sin ϕ) 3
2π = 2π
0
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Эллипсоид ограничен снизу поверхностью z = −c 1− |
|
|
x2 |
− |
y2 |
|
сверху поверхностью |
|||||||||||||||||||||||||||||||||||||||
|
|
a2 |
b2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z = c |
|
x2 |
|
− |
|
y2 |
. |
|
Проекцией эллипсоида на плоскость XOY (область S ) является эллипс |
||||||||||||||||||||||||||||||||||||
|
a2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x2 |
+ |
y2 |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
c 1− |
x2 |
− |
y2 |
|
|
|
|
|
|
|
|
b 1− |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
x2 |
|
y2 |
|
a |
a2 |
|
|
x2 |
|
|
y2 |
||||||||||||||||
|
V = ∫ ∫ds |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
dz = 2c∫ ∫ |
1− |
|
− |
|
ds = 2c ∫dx |
∫ |
|
|
|
|
|
1− |
|
− |
|
dy = |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
a2 |
b2 |
|||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
S |
|
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
−a |
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
−c 1− |
|
|
− |
|
|
|
|
|
|
|
|
|
−b 1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Так как при вычислении внутреннего интеграла x считается постоянной, то можно сделать следующую замену
y = b 1− |
x2 |
sin t; |
dy = b |
|
1− |
x2 |
cos tdt |
|
||||||
a2 |
a2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
, поэтому t меняется от − π доπ |
||||
Переменная y изменяется от −b |
1− |
x2 |
|
до b |
1− |
x2 |
|
|||||||
a2 |
b2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 2 |
||||
31
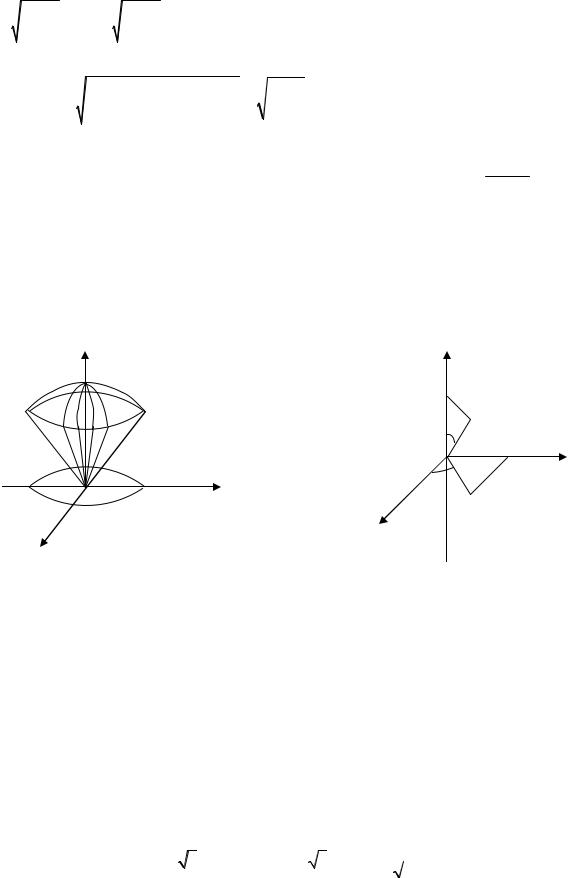
( b 1− |
x2 |
sin t = b |
1− |
x2 |
; |
sin t = 1; t = π ) |
|
a2 |
a2 |
||||||
|
|
|
|
2 |
Подставим в интеграл новые пределы и значения переменных, получим:
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 |
|
|
x2 |
|
x2 |
|
|
|
x2 |
||||||||||
a |
|
2 |
|
|
|
|
|
|
a |
2 |
||||||||||||
V = 2c ∫ |
∫ |
1 |
− |
|
|
− 1 |
− |
|
sin2 t b 1 |
− |
|
|
cos tdt |
dx = 2cb ∫ (1− |
|
)dx ∫ cos2 tdt = |
||||||
−a |
|
|
π |
|
|
a |
|
|
|
a |
|
|
a |
|
|
|
−a |
a |
|
π |
||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
π
|
cb |
a |
|
2 |
|
2 |
2 |
cbπ |
a |
|
2 |
|
2 |
|
cbπ |
|
2 |
|
1 |
|
3 |
|
a |
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
|
∫ |
(a |
|
− x |
|
)dx ∫ (1+ cos 2t)dt = |
|
|
∫ |
(a |
|
− x |
|
)dx = |
|
|
(a |
|
x − |
|
x |
|
) |
|
|
a |
2 |
|
|
a |
2 |
|
|
a |
2 |
|
3 |
|
|||||||||||||||
|
|
−a |
|
|
|
|
− |
π |
|
−a |
|
|
|
|
|
|
|
|
|
|
|
|
−a |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4abcπ
3
|
|
Ответ: |
V = |
4abcπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Если a = b = c , то получим объем шара V = |
4 |
π a3 |
|
|
|
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
|||
2.3.6. Вычислить объем тела, ограниченного поверхностями: сферой x2 + y2 + z2 |
= 1 |
|||||||||||
и конусом z2 = x2 + y2 (z ≥ 0) (рис.42) |
|
|
|
|
||||||||
|
z |
|
|
|
|
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
D |
|
|
|
|
|
|
|
P (ϕ,θ, r ) |
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
r |
|
|
x |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
S |
|
|
y |
ϕ |
|
|
|
|||
|
|
F |
|
|
|
Рис. 43 |
|
|||||
|
|
|
|
|
|
|||||||
|
|
Рис. 42 |
|
|
|
|
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
x
Решение:
Для решения задачи перейдем к сферической системе координат (рис.43) x = r cosϕ sinθ
y = r sin ϕ sinθ
z= r cosϕ
∫∫∫f ( x, y, z ) dxdydz = ∫∫∫ f (r cosϕ sinθ, r sin ϕ cosθ, r cosθ ) r 2 sinθdrdϕdθ
R R
Тогда для нашей задачи имеем:
|
|
|
|
|
|
|
|
|
2π |
π |
|
|
|
|
2π |
π |
|
|
|
|
2π |
π |
|||
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
4 |
|
|
1 |
|
|
1 |
4 |
||||
V = ∫ ∫ ∫dv = ∫ ∫ ∫r 2 sinθ drdϕdθ = ∫dϕ ∫ sinθ dθ ∫r 2 dr = ∫dϕ ∫ sinθ dθ ( |
|
r3 ) |
0 = |
|
∫dϕ ∫ sinθ dθ = |
||||||||||||||||||||
3 |
3 |
||||||||||||||||||||||||
|
|
R |
R |
|
1 2π |
2 |
0 |
0 |
2π |
|
0 |
|
0 |
0 |
|
|
|
|
0 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 2π |
|
4 |
|
|
|
2 |
π |
|
|
|
|
|
|
|
|
|
||||||||
|
|
∫dϕ(−cosθ ) |
π |
|
∫ (− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
0 = |
|
|
|
+1)dϕ = |
|
(1− |
|
|
) = (2 − |
2) |
|
|
|
|
|
|
|||||||
|
3 |
2 |
3 |
2 |
|
|
|
|
|
|
|||||||||||||||
3 |
0 |
|
|
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
Допустим, что 0 ≤ r ≤ 1, т.к. точка P на рис.43 является точкой сферы, а ее радиус
32
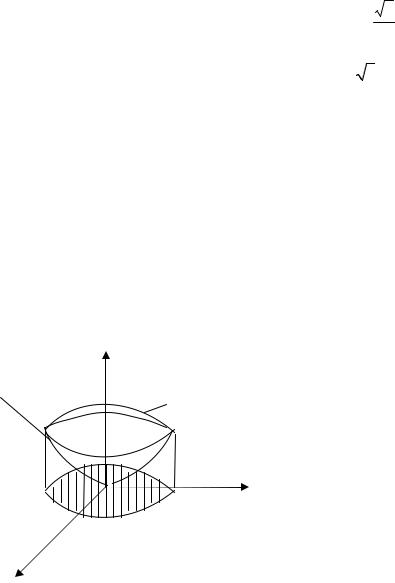
т.к. S есть проекция на XOY круга радиуса 2 , этот круг - есть линия пе-
4 |
|
|
|
|
2 |
||
ресечения сферы и конуса т.е. |
|
|
|
||||
|
|
|
|
|
|
|
|
x2 + y2 + x2 + y2 = 1; |
x2 + y2 |
= |
1 |
есть круг с радиусом |
|
2 |
, треугольник OFD - равно- |
|
|
|
|||||
|
|
2 |
|
2 |
|
||
бедренный т.к. OD2 |
= OF 2 + FD2 , следовательно DOF = π , а значит углы между |
||||||
прямой OD и осью OZ = π |
|
|
|
4 |
|||
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
|
2.3.7. Вычислить интеграл |
∫ ∫ ∫(x2 + y2 )dV , где область R ограничена поверхностями |
||||||
R
z = 4 − x2 − y2 , z = 3(x2 + y2 )
Поверхность z = 3(x2 + y2 ) и z = 4 − x2 − y2 представляют собой параболоиды враще-
ния с осью симметрии OZ |
и вершинами соответственно в начале координат и в точке |
|||
(0, 0, 4) (рис.44). |
|
|
|
|
|
z |
|
|
|
z = 3(x2 + y2 ) |
4 |
|
|
|
|
z = 4 − x2 + y2 |
|
||
|
|
|
||
|
|
|
|
|
0 |
|
y |
|
S |
1 |
|
|
Рис. 44
x
Найдем линию пересечения этих поверхностей
z = 3(x2 + y2 )
z = 4 − x2 − y2
Имеем
3(x2 + y2 ) = 4 − (x2 + y2 )
Откуда
x2 + y2 = 1
Проекция области, заключенной между параболоидами, на плоскость XOY представляет собой круг x2 + y2 = 1− S
33
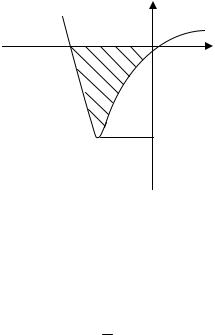
|
|
|
|
|
|
|
|
|
|
|
|
|
z =4−(x2 + y2 ) |
=∫∫(x |
|
|
|
|
|
|
)dxdy z |
|
z =4−(x2 + y2 ) |
|
|
|||||||||
∫ ∫ ∫(x |
2 |
+ y |
2 |
)dxdydz = ∫ ∫(x |
2 |
+ y |
2 |
)dxdy ∫ dz |
2 |
+ y |
2 |
|
= |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
z =3 x2 |
+ y |
2 |
) |
|||||||||||||||||||||||
R |
|
|
|
|
|
S |
|
|
|
|
|
|
z=3( x2 + y2 ) |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 4∫∫(x2 + y2 ) 1− (x2 + y2 ) dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перейдем к полярной системе координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x = r cosϕ, |
|
y = r sin ϕ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
r = 1(x2 + y2 |
= 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2π |
|
|
1 |
|
|
|
2π |
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
2π |
|
2π |
|||||||
|
|
2 |
|
|
2 |
|
|
|
|
3 |
5 |
|
|
4 |
|
6 |
|
|
|
|
|
|
|
|||||||||||
= 4∫ ∫r |
|
(1− r )rdrdϕ = 4 ∫dϕ∫(r |
|
− r )dr = 4 ∫dϕ( |
|
r |
− |
|
|
r |
|
) |
= 4 |
|
|
|
∫dϕ = |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
4 |
6 |
|
0 |
12 |
|
|
3 |
|
|
|||||||||||||||||||||||
S |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Приложение определенного интеграла в геометрии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3.1. Площадь плоской фигуры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3.1.Вычислить площадь фигуры, ограниченной линией y = (x2 + 4x)e−2 x |
и осью OX |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
0 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4, 76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
0
S = − ∫(x2 + 4x)e−2 x dx =
−4
[Интегрируем по частям u = x2 + 4x , du = (2x + 4)dx
dV = −e−2 x dx :V = 1 e−2 x ] 2
= |
1 |
(x2 + 4x)e−2 x |
|
0 − ∫0 (x + 2)e−2 x dx = |
||||||||||
|
||||||||||||||
|
||||||||||||||
2 |
|
|
|
|
−4 |
−4 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|||||||
[еще раз u = x + z, du = dx, |
dV = −e−2 x dx :V = |
e−2 x ] |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
1 |
|
|
|
|
|
1 |
0 |
|
1 |
|
|
|
|
= |
(x + z)e−2 x |
|
−04 − |
∫ e−2 x dx = |
(5 + 3e8 ) |
|||||||||
|
||||||||||||||
|
|
|
||||||||||||
2 |
|
2 |
−4 |
4 |
|
|
|
|||||||
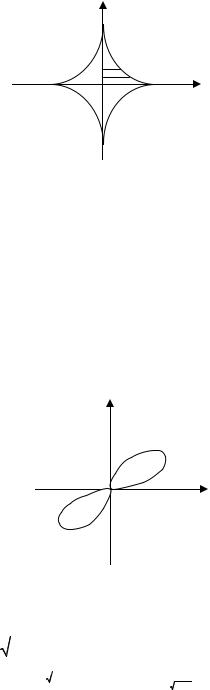
3.2. Вычислить площадь фигуры, ограниченной астроидой x = 2 cos3 t, ó = 2sin3t
(рис. 3.2)
34
y
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
S |
2 |
x |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t2 |
|
|
|
|
|
|
|
|
π |
|
|
π |
|
0 |
|
|
|
|
2 |
|
2 |
||||||
S = ∫ y (t )x'(t)dt = 4∫ 2sin 3t(−6 cos 2 t sin t)dt = 48∫ sin t cos2tdt = 6∫ sin2 2t(1+ cos 2t)dt = |
|||||||||||||
t1 |
π |
|
|
0 |
|
0 |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||
π |
π |
|
|
|
|
|
π |
|
|
||||
2 |
2 |
|
|
|
|
|
3 |
|
3 |
|
|||
|
|
|
|
|
|
2 = |
|
||||||
= 3∫ (1− cos 4t)dt + 6∫ sin3 2t cos 2t = (3t − |
sin 4t + sin3 2t) |
π |
|||||||||||
|
2 |
||||||||||||
0 |
0 |
|
|
|
|
4 |
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|||||
3.3. Найти площадь фигуры, ограниченной кривой (x2 + y2 )2 = 18xy (рис. 3.4)
y
|
|
|
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдем к полярным координатам |
|
|
|
|
||||||||||
r 4 = 18r 2 cosϕ sin ϕ |
|
|
|
|
|
|
|
|
|
|||||
r = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
π |
|
|
|
|
|
π 3 |
|
sin 2ϕ |
|
|
|
|
|
|
|
|
|
π |
|
|
|
2 |
dϕr 2 |
|
0 |
|
2 |
9 |
cos 2ϕ |
= 9 |
||||
S = 2∫ 2 dϕ |
|
∫ |
rdr = ∫ |
|
|
= 9∫ sin 2ϕdϕ = − |
0 |
|||||||
|
|
|
|
|
|
|
|
3 sin 2ϕ |
|
|
2 |
|||
0 |
0 |
0 |
|
|
|
|
0 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
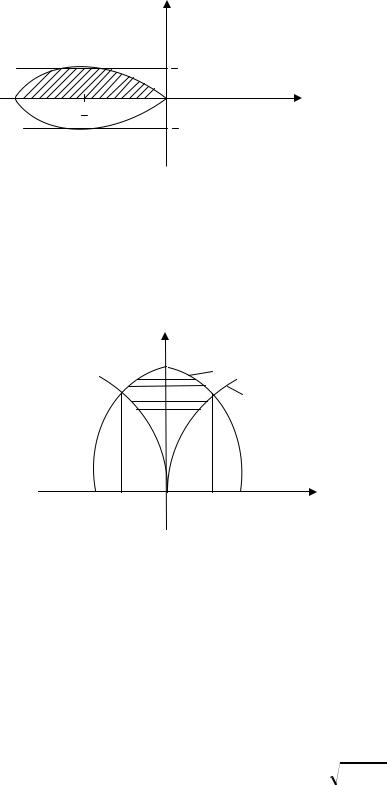
3.4.Найти площадь фигуры, ограниченной линией
x= t2 −1, y = t3 − t (рис.3.4.) (петля)
35
|
S |
y |
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
−1 |
1 |
0 |
x |
|
|||
|
2 |
1 |
|
|
|
4 |
|
Рис. 3.4
Решение:
Ось OX - ось симметрии
0 ≤ z ≤ 1.
1 |
t2 |
|
|
0 |
= 8 |
||
S = −2∫ (t3 − t)2tdt = ∫ y (t )x '(t )dt = − 4(1 t5 − 1 t3 ) |
|
||||||
|
|
|
|
|
1 |
|
|
0 |
5 |
3 |
|
|
15 |
||
|
|
||||||
t1 |
|
|
|
|
|
||
3.5. Вычислить площадь заключенную между кривыми y = 2 − x2 ; y3 = x2 (рис 3.5.)
|
|
|
y |
|
|
|
|||||||
|
2 |
|
|
|
|
y = 2 − x2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
A |
|
|
|
|
|
|
|
|
|
|
y3 = x2 |
||
|
|
|
|
S |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
0 |
x |
|
|
1 |
||
|
|
|
|
Рис. 3.5. |
Решение |
|
|
|
|
y = 2 − x |
|
|
||
|
|
2 |
|
|
Решая систему |
= x2 |
|
находим пределы интегрирования по координате x : |
|
y3 |
|
|
|
|
|
|
|
|
|
x1 = −1, x2 = 1
1 |
y=2−x2 |
1 |
|
x3 |
3 |
|
|
|
1 |
2 |
||
|
|
|||||||||||
S = ∫ dx ∫ dx = ∫ dx (2 − x2 − x2 / 3 ) = 2x − |
|
− |
|
x5 / 3 |
|
|
|
= 2 |
|
|||
|
|
|
||||||||||
−1 |
y=x2 / 3 |
−1 |
|
3 5 |
|
|
|
−1 |
15 |
|||
|
|
|
|
|
|
|
||||||
3.2.Площадь поверхности
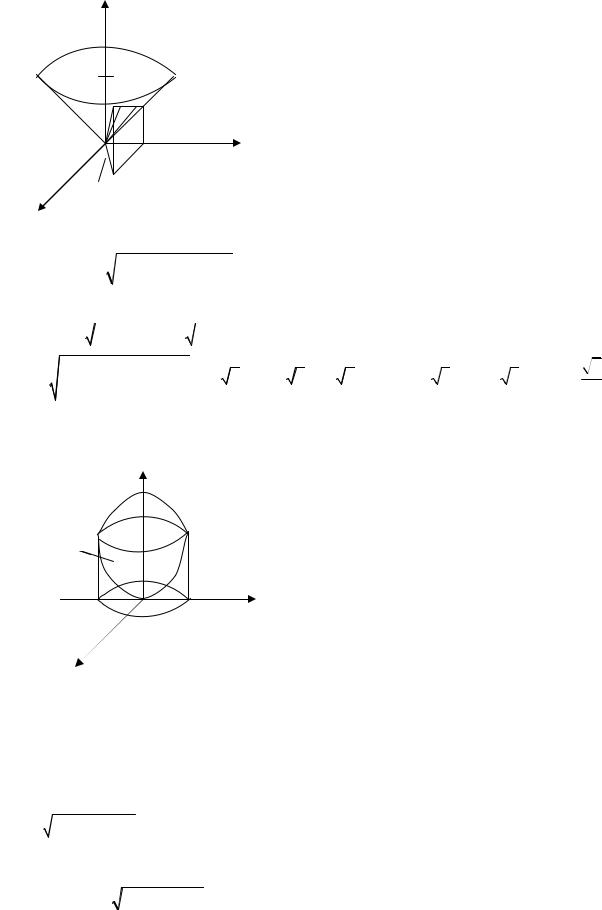
3.6.Найти площадь части поверхности конуса z = 
 x2 + y2 ,вырезанную плоскостями
x2 + y2 ,вырезанную плоскостями
y = x, y = 1, x = 0 (рис. 3.6.)
36
z
0 |
S |
y |
|
1 |
y = x
|
|
x |
|
|
|
|
|
|
|
Рис. 3.6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
S = ∫∫ dq = ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1+ (zx' )2 + (zy' )2 ds |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Q |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dz |
= Zx' = |
|
|
x |
|
|
|
; Z y' = |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 + y2 |
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y = x |
|
1 |
|
x2 |
|
|
1 |
||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dq = 1+ |
|
|
|
|
+ |
|
|
|
|
|
ds = 2ds = ∫∫ 2ds = |
2 ∫ dx ∫ dy = |
2 ∫ xdx = |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
x |
2 |
+ y |
2 |
|
x |
2 |
+ y |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0 |
0 |
0 |
|
2 |
|
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
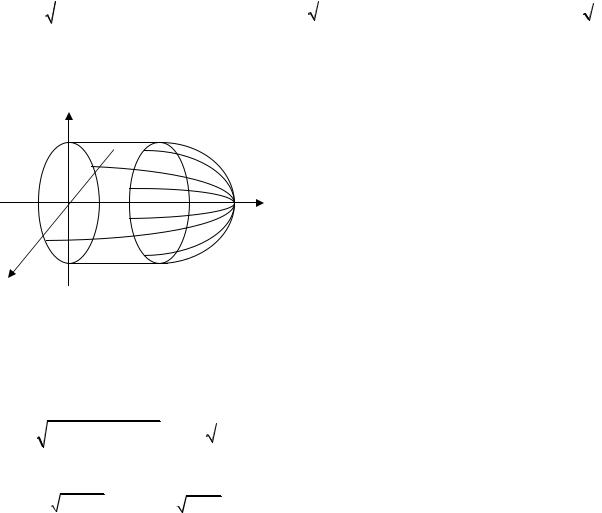
3.7.Вычислить площадь полной поверхности тела, ограниченного параболами z = 2 − x2 − y2 ; z = x2 + y2 (рис.3.7.)
z
 z = 2 − x2 − y2
z = 2 − x2 − y2
z = x2 + y2
y
0 S
Рис. 3.7
x
Решение
S = 2∫∫ dq
Q
z = x2 + y2 ; z 'x = 2x ; z 'y = 2y dq = 
 1+ 4x2 + 4 y2 dS
1+ 4x2 + 4 y2 dS
аналогично
z = 2 − x2 − y2 ; z′ |
= −2x; |
|||
|
|
x |
|
|
z′ |
|
|
|
|
= −2 y; dq = 1+ 4x2 + 4 y2 dS |
||||
y |
|
|
|
|
=
 2 2
2 2
37
проекция на плоскость XOY - S -есть круг x2 |
+ y2 = 1 |
|
|
|
|
|
||||||||
|
|
|
перейдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
к |
2π |
1 |
|
|
|
2π |
2 |
|
2 |
(1+ 4r |
|
S = 2∫∫ |
1+ 4x2 + 4 y2 |
dS |
2 ∫ dϕ∫ |
1+ 4r 2 rdr = 2 |
∫ |
|
||||||||
полярным |
8 |
|
||||||||||||
S |
|
|
0 |
0 |
|
|
|
0 |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
координатам |
|
|
|
|
|
|
|
|
|
|
|
3.8.Вычислить площадь параболы x2 + z2 + y = 8, отсеченной плоскостью
z
2
S
0 |
4 |
y |
8 |
x −2
Рис. 3.8
|
) |
|
dϕ = π |
( |
|
) |
|
|
0 |
|
|||||
2 |
|
1 |
|
5 |
5 |
−1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
y = 4 (рис.3.8.)
Решение:
Уравнение поверхности запишем в виде y = 8 − x2 − z2
Проекция поверхности на плоскость XOZ (S ) - круг x2 + y2 ≤ 4 y 'x = − 2x ; y 'z = − 2z
|
∫∫ |
x |
z |
∫∫ |
|
|
|
S = |
|
1+ ( y ' )2 |
+ ( y ' )2 ds = |
|
1+ 4x2 |
+ 4z2 dxdz = |
|
|
S |
|
|
S |
|
|
|
перейдем к полярной системе координат x = r cosϕ; z = r sin ϕ
=2∫π dϕ∫2 
 1+ 4r 2 rdr = π5 (17
1+ 4r 2 rdr = π5 (17
 17 −1)
17 −1)
0 0
3.2.1. Площади цилиндрической поверхности
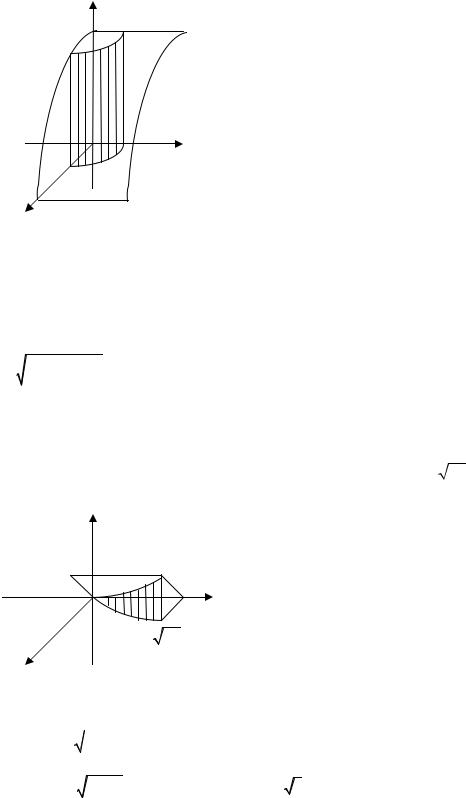
3.9. Найти площадь части цилиндрической поверхности x2 + y2 = 1, заключенной меж-
ду плоскостью z = 0 и поверхностью z = 4 − x2 (рис 3.9.)
38
z
4
y
1
2
x Рис. 3.9
Решение:
S = ∫ zdL =∫(4 − x2 )dL
L L
Уравнение окружности L ( x2 + y2 = 1) запишем в параметрическом виде x = cos t, y = sin t
|
|
dt = dt |
|
|
|
|
|
|
|
|
|
||||
dL = |
(x' )2 + ( y ')2 |
|
|
|
|
|
|
|
|
|
|||||
S = |
2π (4 − cos2 t )dt = |
2π |
4 − |
1+ cos 2t |
dt = |
|
3,5t − |
1 |
sin 2t |
|
|
2π |
= 7π |
||
|
|||||||||||||||
∫ |
|
|
|
|
|
|
|||||||||
|
∫ |
|
|
2 |
|
4 |
|
|
|
|
|||||
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
3.10. Вычислить площадь части параболического цилиндра y = 
 2x , ограниченного плоскостями z = y; x = 2; z = 0 (рис.3.10)
2x , ограниченного плоскостями z = y; x = 2; z = 0 (рис.3.10)
z
z = y |
|
x |
|
0 |
2 |
||
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
2x |
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.10 |
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
y2 ; dL = 1+ y2 dy |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(1+ y2 ) |
|
0 |
= 1 |
(5 5 −1) |
||||
S = ∫ zdL = ∫ y 1+ y2 dy = 1 |
3/ 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
L |
0 |
3 |
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.11. Найти площадь той части поверхности цилиндра x2 + y2 = a2 , которая вырезает-
ся цилиндром x2 + z2 = a2 (рис. 3.11)
39
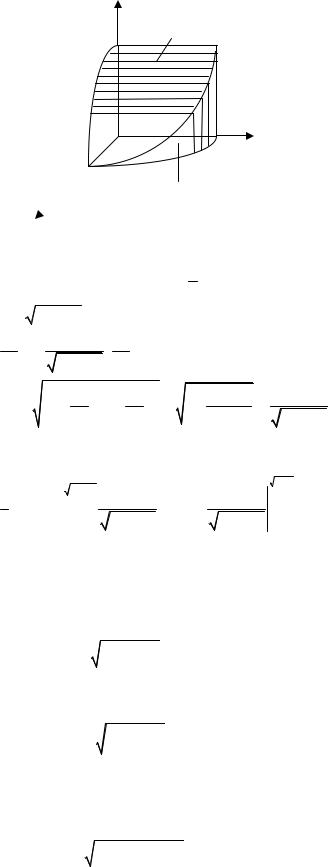
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
x2 + z2 |
= a2 |
|
|
|||
|
|
|
|
|
|
|
a |
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x2 + y2 = a2 |
|
|
|
||||
|
x |
Рис.3.11 |
|
|
|
|
|
|
|
|
||
Решение: |
|
|
|
|
|
|
|
|
|
|
||
На рис. |
3.11 |
изображена 1 |
часть поверхности. Уравнение поверхности имеет вид |
|||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
y = |
a2 − x2 , |
поэтому |
|
|
|
|
|
|
|
|||
dy = − |
x |
|
; dy = 0 |
|
|
|
|
|
|
|
||
dx |
|
a2 − x2 |
dz |
|
|
|
|
|
|
|
|
|
|
|
dy |
2 |
dy 2 |
|
|
|
x2 |
2 = |
|
a |
|
dq = 1+ |
|
+ |
= 1+ |
a |
2 |
− x |
|
a2 − x2 |
||||
|
|
dx |
|
dz |
|
|
|
|
||||
Область интегрирования представляет собой четверть круга, т.е. определяется усло- |
||||||||||||
виями x2 + z2 |
≤ a2 ; x ≥ 0; z ≥ o, |
тогда |
|
|
||||||||
|
|
a2 −x2 |
|
|
|
|
|
|
|
|
a2−x2 |
|
|
a |
|
|
a |
|
|
|
|
|
a |
||
1 Q = ∫ dx ∫ |
|
a |
|
dz = a ∫ |
|
|
z |
|
|
dx = a∫ dx = a2 |
||
8 |
0 |
0 |
|
a2 − x2 |
0 |
|
a2 − x2 |
0 |
0 |
|||
3.2.2. Площадь поверхности вращения |
||||||||||||
Если поверхность образована вращением линии y = y ( x) , x [a, b] |
вокруг оси |
||
OX (рис 3.12), то ее площадь Q вычисляется по следующей формуле: |
|
||
Q = 2π ∫ab y(x) |
|
dx |
|
1+ ( y 'x )2 |
(3.1) |
||
При вращении линии x = x ( y ) , y [c, d ] |
вокруг оси OY (рис. 3.13.) формула определе- |
||
ния площади вращения имеет вид: |
|
||
d |
|
|
|
|
|
||
Q = 2π ∫ x ( y ) 1+ (x 'y )2 dy |
(3.2.) |
||
c |
|
||
Если линия задана параметрически уравнением x = x (t ) , y = y (t ) , t [t1 , t2 ] , то
площадь поверхности, образованной вращением ее относительно оси ox , определяется формулой:
Q = 2π t2 |
y (t ) |
|
|
dt |
|
( x ' )2 |
+ ( y ')2 |
(3.3) |
|||
∫ |
|
t |
t |
|
|
t1 |
|
|
|
|
|
а если вокруг оси OY ,то
40
