Ответ: ; .

Задание №8 .

Непрерывная случайная величина задана функцией распределения :

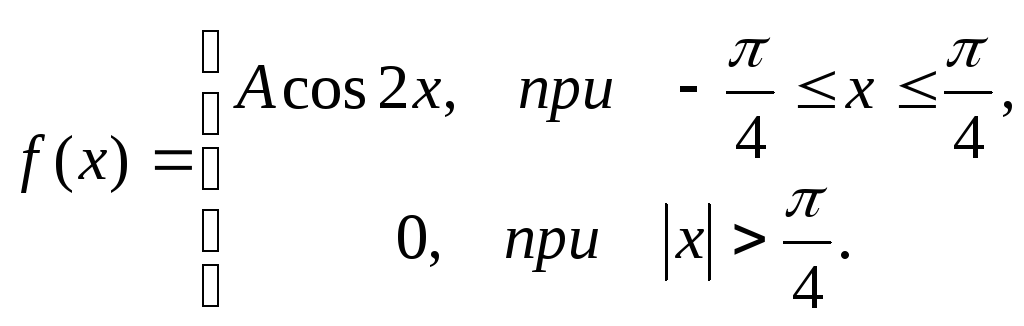
Определить коэффициент , найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величинапопадет в интервал. Найти математическое ожидание и дисперсию.

Решение.

Найдем коэффициент , используя свойство функции плотности распределения:.

.

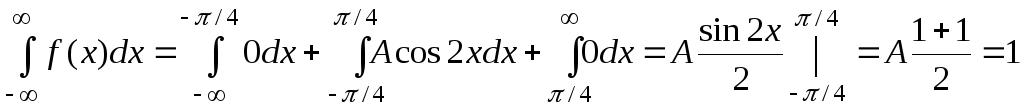Итак, . Найдем функцию распределения:

1) на интервале :;

2) на интервале :

;

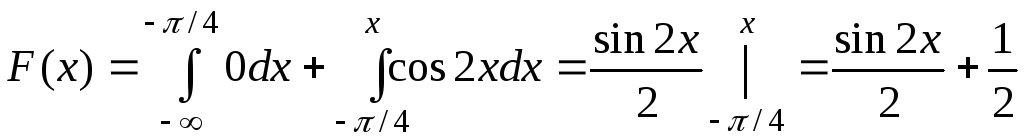3) на интервале :

.

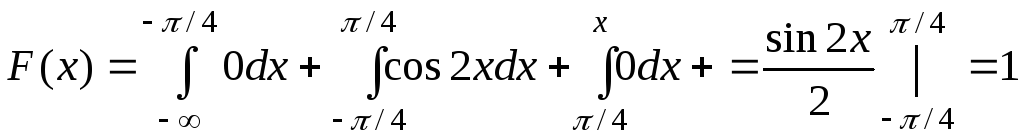Таким образом,

;

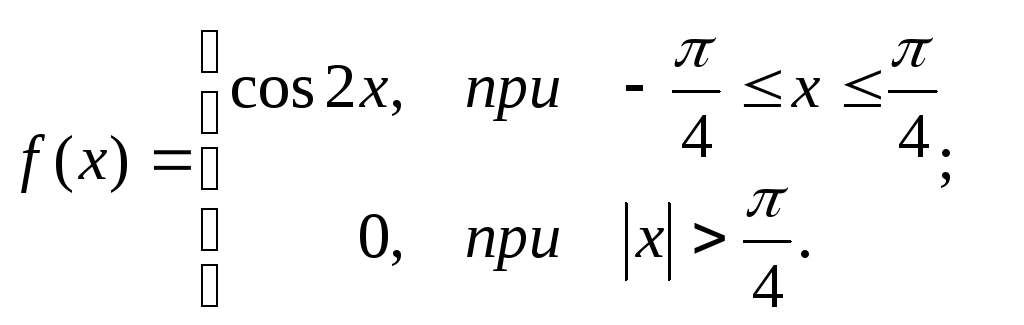
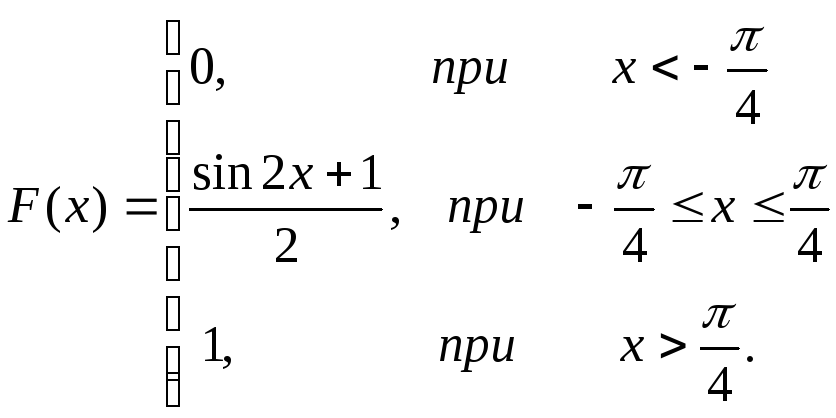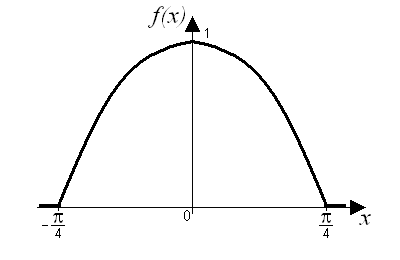
Построим график плотности распределения :

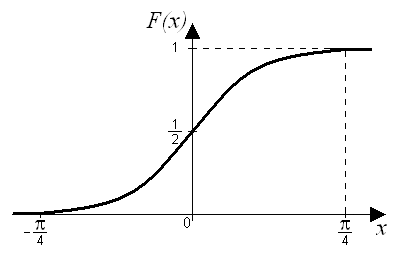
Построим график функции распределения :

Найдем вероятность попадания случайной величины в интервал

.

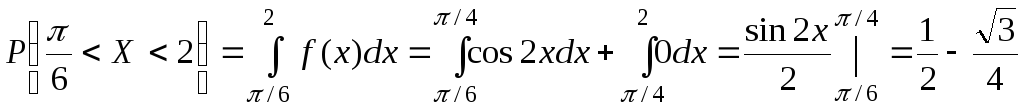Вероятность можно найти и другим способом:

.

Вычислим математическое ожидание .

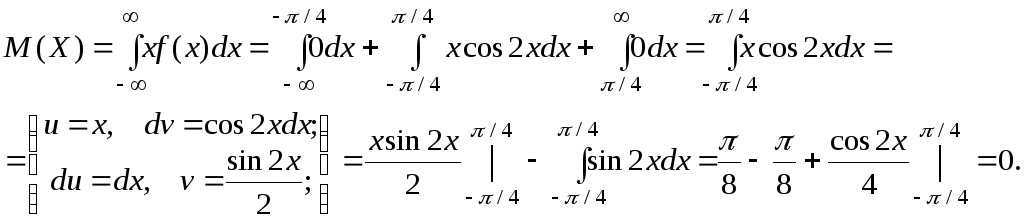
Найдем дисперсию .

,

.

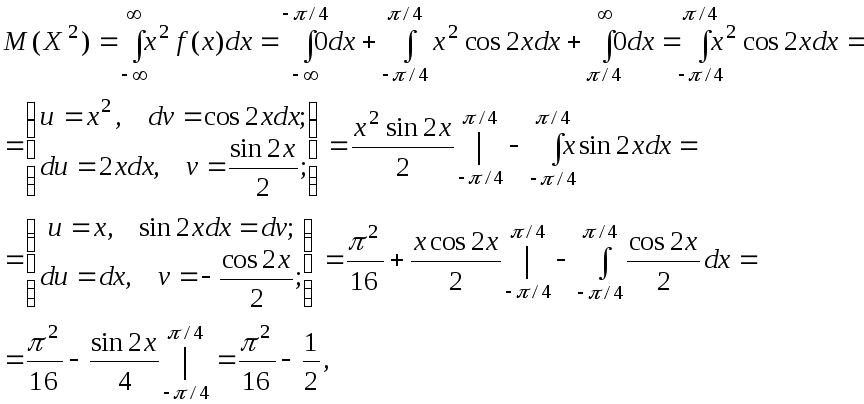
Ответ: ; , ,

, .

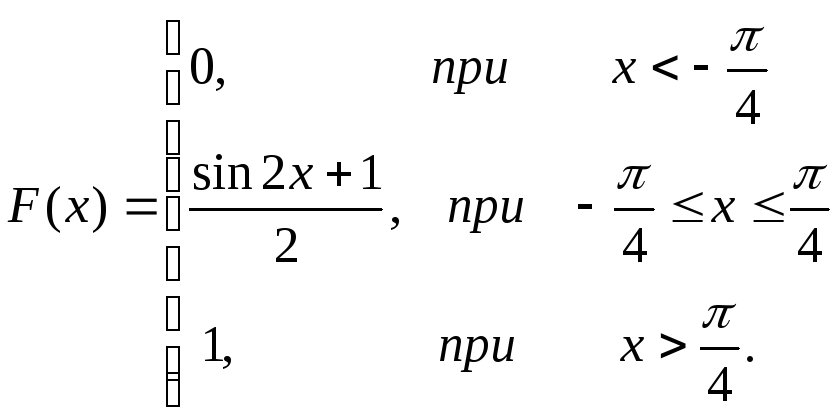Задание №9 .

Нормально распределенная величина задана своими параметрами: математическое ожиданиеи среднеквадратическое отклонение. Найти вероятность того, что а) значения случайной величины попадут в интервал, б) случайная величинаотклонится по модулю от математического ожидания не более чем на.

Решение.

1. Так как случайная величина 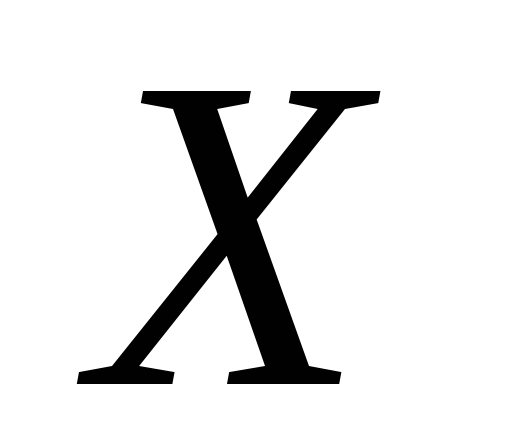распределена по нормальному закону, то вероятность, что значения этой случайной величины попадут в интервал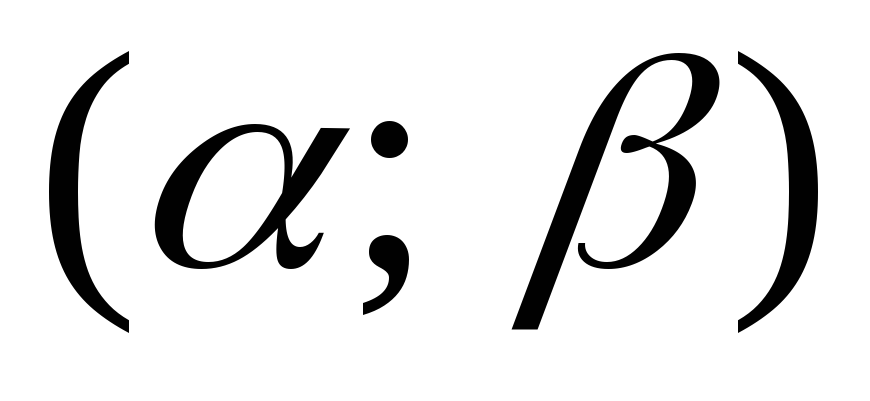, находится по формуле:

,

где - математическое ожидание,- среднеквадратическое отклонение, а значения функциинаходим по таблице 4.

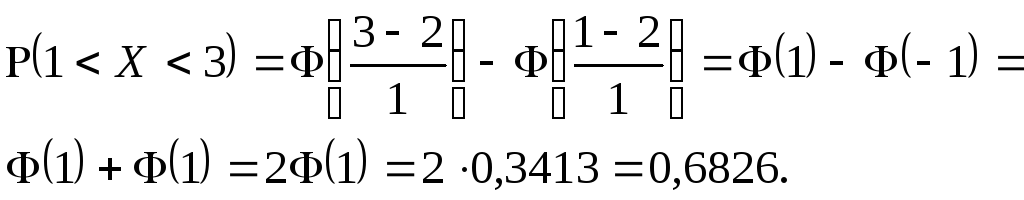
2. Вероятность, что нормально распределенная величина 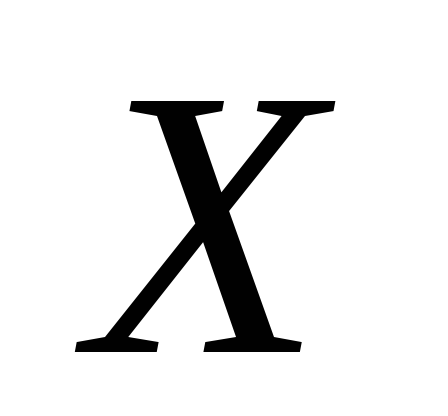отклонится по модулю от математического ожиданияне более чем нанаходится по формуле:

.

Ответ: а) , б) .

Приложение №1.

Лабораторная работа

ФОРМУЛА БАЙЕСА

Основные определения и формулы

Случайным событием называется такое событие, которое может произойти или не произойти в результате некоторого опыта.

Случайные события называют несовместными в данном испытании, если появление одного из них исключает появление других событий в одном и том же испытании.

Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие несовместное с ними.

Вероятностью Р события А называется отношение числа m благоприятствующих случаев к числу всех возможных случаев

(1)

Сумма вероятностей случайных событий B₁, B₂,…B_n ,

образующих полную группу, равна единице

Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или не произошло событие В.

Вероятность того, что произошло событие А при условии,что произошло событие В, будем обозначатьP(A/B) и называть условной вероятностью события А при условии В.

Рассмотрим полную группу несовместных событий В₁, В₂, …, В_n, вероятности появления которых P(B₁), P(B₂), …, P(B_n). Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Событие А может наступить в каком-либо опыте вместе с одной из гипотез событий В₁, В₂, …, В_n. Вероятность события А вычисляется по формуле полной вероятности

(2)

После опыта (апостериорно) стало известно, что событие А появилось, следует выяснить, вместе с какой из гипотез B₁,…, B_n оно произошло. По постановке задача напоминает диагностику причины по известному следствию.

P(Bi), i=1,…n - априорные (доопытные) вероятности гипотез

P(Bi / A), i=1,…n - апостериорные вероятности гипотез (сформировавшиеся после опыта)

Найдем апостериорные вероятности гипотез P(Bi / A), i=1,…n.

По формуле умножения вероятностей найдем вероятность совмещения событий B и А

P(B_i A)=P(B_i) P(A / B_i)=P(A) P(B_i/A).

Из последнего равенства выразим апостериорную вероятность гипотезы В

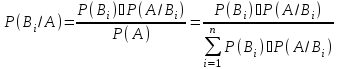
(3)

Получили формулы Байеса. Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, т.е. провести коррекцию вероятностей априорных гипотез, используя экспериментальные данные.