Нормальное распределение случайной величины

Случайная величина называется нормально распределенной, если ее плотность вероятности и функция распределения имеют вид:

, ,

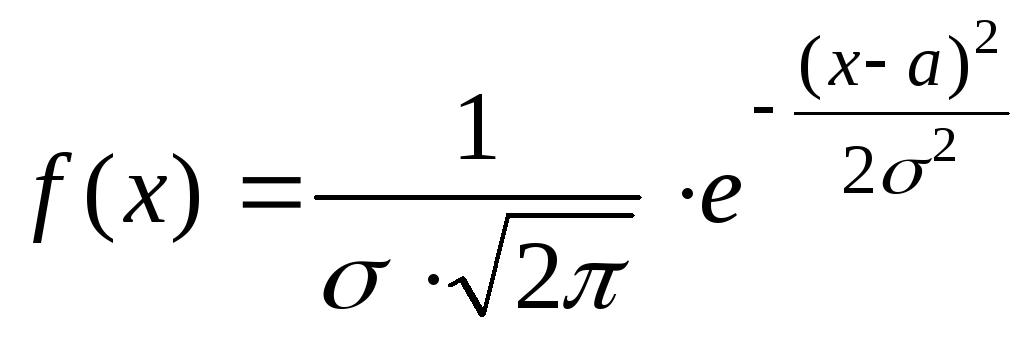где - функция Лапласа,и- параметры нормального распределения:

(математическое ожидание), (среднеквадратическое отклонение).

Пример 15.

Прибор состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном испытании равна 0,2. Составить закон распределения числа отказавших элементов в одном опыте.

Решение.

Пусть случайная величина - число отказавших деталей в одном опыте:

: , , , .

Вероятность отказа указанного () числа элементов вычисляется по формуле Бернулли, так как вероятности отказа каждого элемента равны между собой

,

,

,

.

Проверим выполнение условия :

=1.

Составим ряд распределения случайной величины .

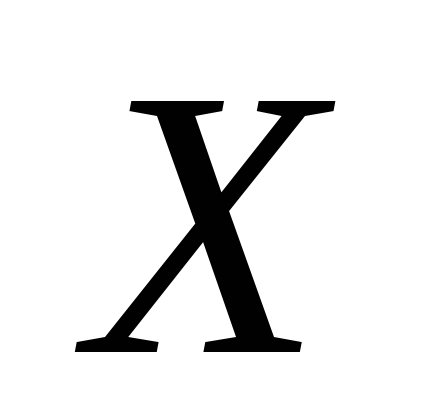
	0	1	2	3
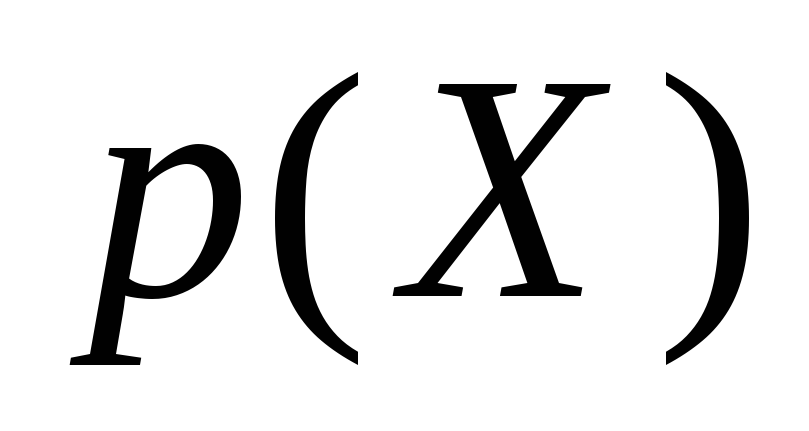
	0,512	0,384	0,096	0,008

Пример 16.

Случайная величина задана функцией распределения:

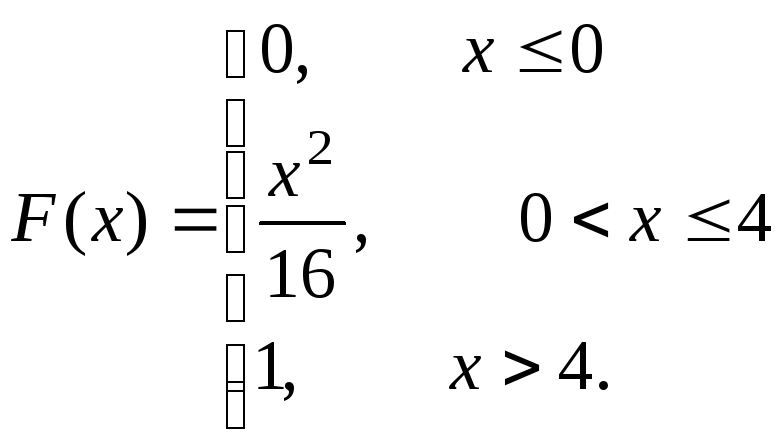
Найти функцию плотности распределения , математическое ожидание, дисперсию, вычислить вероятность события, построить графики функцийи.

Решение.

Функция плотность распределения и функция распределениясвязаны равенством. Следовательно,

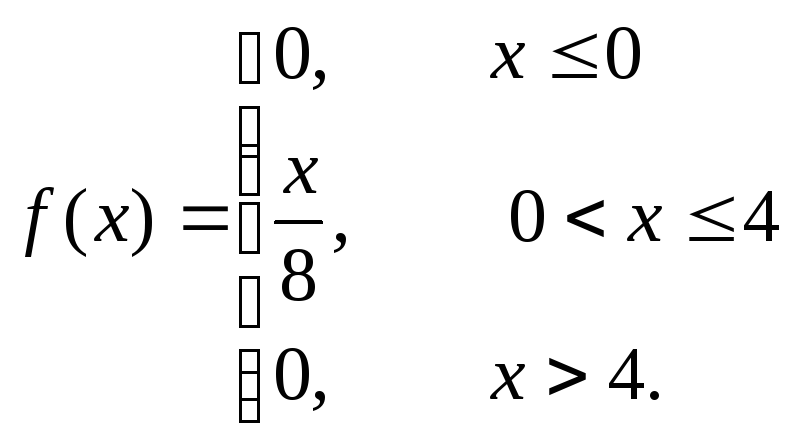
Построим график плотности распределения :

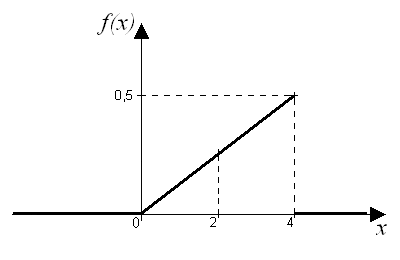
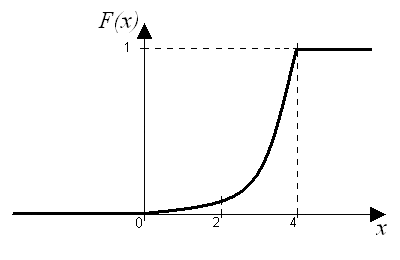
Построим график функции распределения :

Найдем математическое ожидание и дисперсию.

,

.

События ипротивоположны, следовательно, тогда.

Рассмотрим решение задач типового варианта. Задание №1 .

На полке стоят 10 книг, 7 из них по математике. Найти вероятность того, что среди 6-ти взятых наудачу книг 4 по математике.

Решение.

Пусть событие – среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятностьравна отношению– числа исходов, благоприятствующих событию, к– числу всех элементарных исходов:

.

Общее число всех всевозможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 книг из 10 имеющихся, т.е. числу сочетаний из 10 элементов по 6 ().

Определим – число исходов, благоприятствующих событию. Четыре книги можно взять из 7 книг по математикеспособами; при этом остальные () книги должны быть не по математике. Взять же 2 книги нематематические из () нематематических книг можноспособами. Следовательно, число благоприятствующих исходов. Таким образом, учитывая, что, получаем:

.

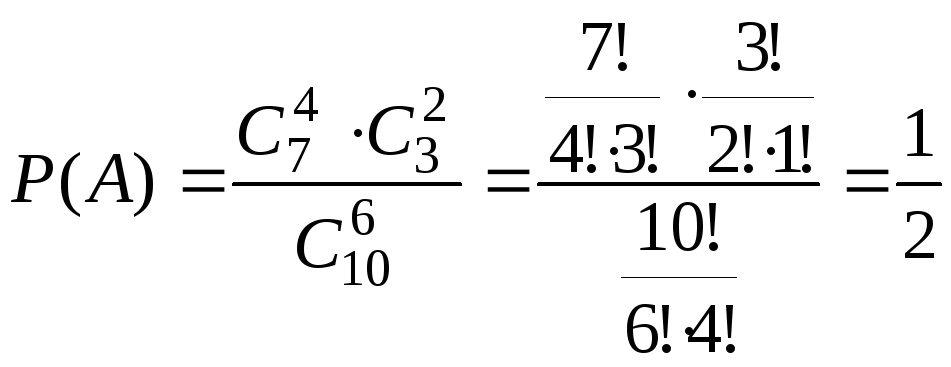Ответ: . Задание №2 .

Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна , а для второго – . Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Решение.

Пусть событие – попадание в цель первым стрелком, событие – вторым, промах первого стрелка – событие , промах второго – событие . Тогда ,,,.

Вероятность того, что первый стрелок попадет в мишень, а второй – нет, равна .Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна . Тогда вероятность попадания в цель только одним стрелком равна .

Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны: ;.Тогда вероятность того, что в цель попадет только один стрелок равна: .