§ 4. Условия принадлежности прямой линии плоскости
Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие этой плоскости или через одну точку этой плоскости, параллельно прямой, лежащей в этой плоскости.
Задача
Провести прямую, принадлежащую данной плоскости. Рассмотрим пример на основе применения определения, когда плоскость задана разными способами (табл. 5.5).
Таблица 5.5
|
Условие |
Комплексный чертеж |
|
Плоскость задана тремя точками A, B, C. Решение: провести прямую m через любые две точки (в частности, A и B) |
|
|
Плоскость задана точкой А и прямой а. Решение: 1) на прямой а выбираем любую точку L (L2); строим L1 2) через А и L проводим прямую b |
|
|
Плоскость
задана двумя пересекающимися прямыми:
а Решение: 1) выбираем произвольные точки на прямой a L(L1L2), и на прямой b – M (M1M2). 2) проводим прямую c через эти точки |
|
|
Плоскость задана двумя параллельными прямыми а || b. Решение:
1)
выбираем на прямых по одной произвольной
точке K 2) через одноименные проекции K и L проводим прямую с |
|
|
Плоскость задана плоской фигурой. Решение: 1) на любых сторонах треугольника выбираем произвольные точки K и L; 2) через одноименные проекции проводим проекции прямой а |
|
b = K.
a
и L
b;
Задача № 1
Определить принадлежность прямой линии плоскости, если дана плоскость D ABC (D A1B1C1, D A2B2C2) и прямая a (a1a2) (рис. 5.2).
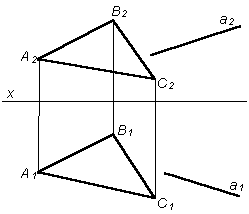
Рис. 5.2
Задача № 2
Достроить фронтальную проекцию четырехугольника; плоскость четырехугольника задана горизонтальной проекцией и тремя точками фронтальной проекции (рис. 5.2–5.4).
|
|
|
|
|
Рис. 5.2 |
Рис. 5.3 |
Рис. 5.4 |
Задача № 3
Достроить вторую проекцию параллелограмма (рис. 5.5).
Рис. 5.5
Задача № 4
Достроить вторую проекцию пятиугольника (рис. 5.6).
Рис. 5.6
§ 5. Прямые особого положения в плоскости
Прямыми особого положения в плоскости являются горизонталь h, фронталь f и линии наибольшего наклона к плоскостям проекций. Рассмотрим графическое изображение этих линий (табл. 5.6).
Таблица 5.6
|
Определение |
Комплексный чертеж |
|
1. Горизонталью плоскости называется прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций, обозначаемая h. Построение горизонтали начинается с фронтальной проекции h2. Все горизонтали одной плоскости между собой параллельны. Горизонталь есть геометрическое место точек плоскости, удаленных от плоскости p1 на одно и то же расстояние |
|
|
2. Фронталью плоскости называется прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций, обозначаемая f. Все фронтали одной плоскости параллельны между собой. Фронталь плоскости – это геометрическое место точек, удаленных от плоскости p2 на одно и то же расстояние |
|
|
3. Линиями наибольшего наклона данной плоскости к плоскостям проекций называются линии, лежащие в плоскости и перпендикулярные горизонтали, фронтали или ее профильной прямой. В первом случае определяется наклон данной плоскости к плоскости p1, во втором – к p2, в третьем – к p3. Линия наибольшего наклона к p1 называется линией наибольшего ската (ЛНС). Построение ЛНС начинается с ее горизонтальной проекции n1, так как согласно свойству проецирования прямого угла, угол 900 между ЛНС и h1 на p1 проецируется без искажения |
|
Задача № 1
1. Провести фронталь в плоскости, заданной двумя параллельными прямыми: a (а || b) (табл. 5.7).
Таблица 5.7