§ 3. Положение плоскости относительно плоскостей проекций
Плоскости в пространстве могут занимать общее (табл. 5.2) и частное положение (табл. 5.3 и табл. 5.4).
Плоскость общего положения
Таблица 5.2
|
Определение |
Наглядное изображение |
Комплексный чертеж |
|
Плоскость, не перпендикулярную ни к одной из плоскостей проекций, называют плоскостью общего положения |
|
|
Плоскости частного положения
Плоскостью частного положения называют плоскость, которая либо перпендикулярна, либо параллельна одной из плоскостей проекций. Плоскости частного положения могут быть проецирующими (табл. 5.3) и плоскостями уровня (табл. 5.4).
Таблица 5.3
Плоскости проецирующие
|
Определение |
Наглядное изображение |
Комплексный чертеж |
|
Горизонтально-проецирующей
плоскостью называют плоскость,
перпендикулярную к плоскости проекций
|
|
|
(D
ABC)^
p1.
Любой элемент, лежащий в этой плоскости,
проецируется на плоскость p1
в прямую линию; горизонтальная проекция
D
A1B1C1
есть прямая линия на плоскости p1;
угол b
есть угол наклона этой плоскости к
плоскостям p2.
Он проецируется на горизонтальную
плоскость без искажения
|
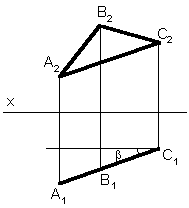
Фронтально-проецирующей плоскостью называют плоскость, перпендикулярную к плоскости проекций p2. Любой элемент, лежащий в этой плоскости, проецируется на плоскость p2 в прямую линию; фронтальная проекция D A2B2C2 есть прямая линия на плоскости p2. Угол a есть угол наклона этой плоскости к плоскости p1, он проецируется на плоскость p2 без искажения |
|
|
|
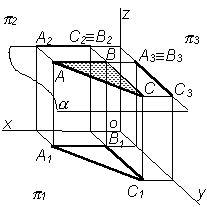
Профильно-проецирующей плоскостью называют плоскость перпендикулярную к плоскости проекций p3. Любой элемент, лежащий в этой плоскости, проецируется на профильную плоскость проекций в прямую линию. Профильная проекция D A3B3C3 есть прямая линия плоскости p3. Углы a и b есть углы наклона этой плоскости к p1 и p2 |
|
|
Таким образом, если плоскость перпендикулярна одной из плоскостей проекций, то на эту плоскость она проецируется в виде прямой линии.
Задача
Построить комплексный чертеж фронтально-, профильно- и горизонтальнопроецирующих плоскостей, если они заданы:
а) тремя точками;
б) прямой и точкой, не принадлежащей данной прямой;
в) двумя пересекающимися прямыми;
г) двумя параллельными прямыми.
Таблица 5.4
Плоскости уровня
|
Характеристика |
Наглядное изображение |
Эпюр |
|
Фронтальная плоскость – это плоскость, параллельная плоскости p2. Эта плоскость пересекает плоскость p1 параллельно оси ОХ, а плоскость p3 – по линии, параллельной оси OZ |
|
|
|
Горизонтальная плоскость – это плоскость, параллельная плоскости проекции p1. Эта плоскость пересекает плоскость p2 параллельно оси ОХ, а плоскость p3 – параллельно оси ОУ |
|
|
|
Профильная плоскость – это плоскость, параллельная плоскости p3. Эта плоскость пересекает плоскости проекций p1 и p2 по линиям, параллельным оси Z |
|
|
Таким образом, если плоскость параллельна какой-либо плоскости проекций, то на эту плоскость она проецируется в натуральную величину, а две ее другие проекции есть прямые линии параллельные осям проекций.
Задача
Постройте комплексный чертеж плоскости уровня (горизонтальной, фронтальной, профильной), если они заданы:
а) тремя точками;
б) прямой и точкой, не лежащей на прямой;
в) двумя пересекающимися прямыми;
г) двумя параллельными прямыми;
д) плоской фигурой.