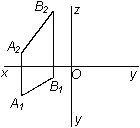- •Начертательная геометрия
- •Оглавление
- •Введение
- •Общие требования и методические рекомендациипо изучению курса “начертательная геометрия”
- •Методические указания по выполнению расчетно-графических работ
- •Глава 1Метод проекций
- •§ 1. Геометрические образы
- •Обозначение отношений между геометрическими образами
- •Обозначения теоретико-множественные
- •§ 2. Способ проецирования
- •1. Проецирование центральное
- •2. Проецирование параллельное
- •§ 3. Свойства ортогональных проекций
- •§ 4. Обратимость чертежа. Метод Монжа
- •§ 2. Точка в системе двух плоскостей проекций p 1 и p 2
- •§ 3. Образование комплексного чертежа (эпюра)
- •§ 4. Характеристика положения точки в системе p 1 и p 2
- •Пример изображения точек в системе двух плоскостей проекций
- •Пример изображения точек, принадлежащих плоскостям p 1 и p 2
- •Задача № 1.
- •§ 5. Система трех взаимно перпендикулярных плоскостей
- •§ 6. Точка в системе p1, p2, p3
- •1. Алгоритм построения наглядного изображения точки, заданной координатами (рис. 2.30):
- •Вопросы для самоанализа
- •Основные понятия, которые необходимо знать:
- •Способы деятельности, которыми надо уметь пользоваться:
- •Контрольные задания
- •Расчетно-графическая работа № 1.
- •§ 2. Прямая общего положения в системе трех плоскостей проекций p 1, p 2, p 3
- •§ 3. Прямые частного положения
- •Прямые уровня
- •Проецирующие прямые
- •§ 4. Построение третьей проекции отрезка по двум заданным
- •§ 5. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций
- •§ 6. Определение натуральной величины отрезка прямой общего положения
- •§ 7. Принадлежность точки прямой
- •Способы деятельности, которыми надо уметь пользоваться:
- •§ 2. Определение видимости прямых относительно плоскостей проекций
- •Алгоритм построения прямых пересекающихся
- •Алгоритм построения прямых параллельных
- •Способы деятельности, которыми необходимо владеть:
- •§ 3. Положение плоскости относительно плоскостей проекций
- •Плоскость общего положения
- •Плоскости частного положения
- •Плоскости проецирующие
- •Плоскости уровня
- •§ 4. Условия принадлежности прямой линии плоскости
- •§ 5. Прямые особого положения в плоскости
- •Алгоритм построения фронтали
- •§ 6. Принадлежность точки плоскости
- •Алгоритм построения второй проекции точки к
- •Глава 6Взаимное положение двух плоскостей, прямой линии и плоскости
- •§ 1. Взаимное положение двух плоскостей
- •Алгоритм построения плоскости, параллельной данной
- •Алгоритм построения линии пересечения горизонтально проецирующей плоскости р с плоскостью общего положения q(d авс)
- •§ 2. Линия пересечения двух плоскостей общего положения
- •Алгоритм построения линии пересечения mn плоскости q(a|| b) и плоскости (d авс) общего положения при помощи двух вспомогательных фронтально-проецирующих секущих плоскостей
- •Расчетно-графическая работа № 4
- •§ 4. Пересечение прямой линии с плоскостью общего положения
- •Алгоритм пересечения прямой линии с плоскостью общего положения
- •§ 5. Перпендикулярность прямой и плоскости
- •Алгоритм построения перпендикуляра к плоскости
- •§ 6. Перпендикулярность двух плоскостей
- •Алгоритм построения плоскости, перпендикулярной данной
- •Вопросы для самоанализа
- •Основные понятия, которые необходимо знать:
- •Тесты Тесты к главе 1
- •Тесты к главе 2
- •Тесты к главе 3
- •Тесты к главе 4
- •Тесты к главе 5
- •Тесты к главе 6
- •Заключение
- •Краткий словарь специальных терминов и определений
- •Рекомендуемый библиографический список
§ 4. Построение третьей проекции отрезка по двум заданным
В нашем примере мы будем рассматривать построение прямой общего положения в первой четверти (табл. 3.3).
Таблица 3.3
|
Вербальная форма |
Графическая форма |
|
1. Прямая AB задана двумя проекциями А1В1 и А2В2. Необходимо построить третью проекцию А3В3 |
|
|
2. Построить третью проекцию точки А – А3: |
|
|
а) на оси z и y отложить координаты точки А: Az и Aу |
a)
|
|
б) построить Ау для профильной проекции |
б)
|
|
в) построить перпендикуляры из Аz и Ay. Обозначить полученную профильную проекцию точки А3 |
в)
|
|
3. Построить третью проекцию точки В3: |
|
|
а) на осях z и y отложить координаты точки В: Вz и Ву |
а)
|
|
б) построить Ву для профильной проекции точки В |
б)
|
|
в) построить перпендикуляры: ВzВ3 ^ z. ВyВ3 ^ y. Обозначить профильную проекцию точки В3 |
в)
|
|
4. Соединить полученные проекции А3 и В3 – это и будет проекция отрезка АВ на плоскость p 3 |
|
Задача № 1
При решении задач использовать алгоритм построения третьей проекции прямой по двум заданным (табл. 3.3).
1. По двум заданным проекциям построить третью на рис. 3.1–3.9:
|
|
|
|
|
Рис. 3.1. |
Рис. 3.2. |
Рис. 3.3. |
|
|
|
|
|
Рис. 3.4. |
Рис. 3.5. |
Рис. 3.6. |
|
|
|
|
|
Рис. 3.7. |
Рис. 3.8. |
Рис. 3.9. |
Задача № 2
Определить, на каком из комплексных чертежей данная прямая является натуральной величиной отрезка. Где можно определить углы наклона прямой к плоскостям проекций (рис. 3.1–рис. 3.9)?
§ 5. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций
Построение проекций отрезка прямой общего и частного положения позволяет решать не только позиционные задачи (расположение относительно плоскостей проекций), но и метрические – определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям. Рассмотрим способ решения такой задачи для отрезка общего положения.
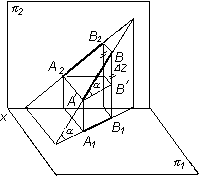
Пусть дан отрезок АВ общего положения относительно плоскостей p1 и p2. АВ'В – прямоугольный треугольник (рис. 3.10), в котором катет АВ' = А1В1 (проекции отрезка АВ на плоскость p1), а катет ВВ' равен z – разности расстояний точек А и В до плоскости p1. Угол a в прямоугольном треугольнике АВ'В определяет угол наклона прямой АВ к плоскости p1.
Рассмотрим
треугольник ВА'А (рис. 3.11), где катет ВА'
равен проекции А2В2
(ВА' = А2В2),
а второй катет АА' равен D
y – разности расстояний точек А и В от
плоскости p
2.
Угол ![]() в
прямоугольном треугольнике ВАА'
определяет угол наклона прямой АВ к
плоскостиp2.
в
прямоугольном треугольнике ВАА'
определяет угол наклона прямой АВ к
плоскостиp2.
Таким образом, натуральная длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – алгебраической разности расстояний от концов отрезка до одной из плоскостей проекций.
|
|
|
|
Рис. 3.10 |
Рис. 3.11 |