1.Понятие о форме и размерах земли. Геоид и референц - эллипсоид Красовского.

Землю в первом приближении можно считать шаром. Во втором приближении Землю принимают за эллипсоид вращения; в некоторых исследованиях ее считают двухосным эллипсоидом. Геоид- тело принятое за теоретическую фигуру Земли, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями. Так, для приближенных вычислений Землю принимают за  шар с радиусом 6371 км. Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a  большая полуось, b  малая полуось,   полярное сжатие и e – первый эксцентриситет меридианного эллипса, где 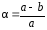и.

Рис. 2.1. Меридианный эллипс: Рс – северный полюс; Рю – южный полюс

Различают общеземной эллипсоид и референц-эллипсоид.

Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США).

Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются.

В России с 1946 г. в качестве референц-эллипсоида  используется эллипсоид Красовского с параметрами: а = 6 378 245 м, a = 1/ 298,3.

2.Системы координат в геодезии. Абсолютные и относительные высоты.

Системы координат, применяемые в геодезии

Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.

Пространственные прямоугольные координаты. Начало системы координат расположено в центре Oземного эллипсоида (рис. 2.2).

Рис. 2.2. Земной эллипсоид и координаты: Х, Y , Z – пространственные прямоугольные; B, L, H  геодезические; G  Гринвич

Ось Zнаправлена по оси вращения эллипсоида к северу. ОсьХлежит в пересечении плоскости экватора с начальнымгринвичским меридианом. ОсьYнаправлена перпендикулярно осямZиXна восток.

Геодезические координаты. Геодезическими координатами точки являются ее широта, долгота и высота (рис. 2.2).

Геодезической широтой точкиМназывается уголВ, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.

Широта отсчитывается от экватора к северу и югу от 0до 90и называется северной или южной. Северную широту считают положительной, а южнуюотрицательной.

Плоскости сечения эллипсоида, проходящие через ось OZ, называютсягеодезическими меридианами.

Геодезической долготойточкиМназывается двугранный уголL, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.

Долготу отсчитывают от начального меридиана в пределах от 0до 360на восток, или от 0до 180на восток (положительные) и от 0до 180на запад (отрицательные).

Геодезической высотой точкиМявляется ее высотаНнад поверхностью земного эллипсоида.

Геодезические координаты с пространственными прямоугольными координатами связаны формулами

X = (N + H) cosB cosL, Y = (N+H) cosB sinL, Z = [(1  e²) N+H] sinB,

где eпервый эксцентриситет меридианного эллипса иN  радиус кривизны первого вертикала. При этомN=a/(1e²sin²B)^1/2. Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами. Отметим, что наряду с геодезическими существуют еще астрономические широта и долгота.Астрономическая широтаэтоугол, составленный отвесной линией в данной точке с плоскостью экватора.Астрономическая долгота – угол между плоскостями Гринвичского меридиана и проходящего через отвесную линию в данной точке астрономического меридиана. Астрономические координаты определяют на местности из астрономических наблюдений.Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности называется уклонением отвесной линии.

Обобщением геодезических и астрономических координат является термин – географические координаты.

Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.

Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют собой сферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6. Центральный меридиан каждой зоны называется осевым. Нумерация зон идет от Гринвича к востоку.

Рис. 2.3. Деление поверхности Земли на координатные зоны: G– Гринвич

Долгота осевого меридиана зоны с номером N равна:

₀ = 6 N  3 .

Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор  за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.

Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х0=0; у0=500 км).

Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x₀ = 0, y₀ = 500 км, что равносильно смещению оси х к западу на 500 км.

Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате yслева приписывают номер координатной зоны.

Пусть например, координаты точки Аимеют вид:

x_А = 6 276 427 м ,y_А= 12 428 566 м

Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y  500 км) 12-ой координатной зоны, на расстоянии 500000  428566 = 71434 м от осевого меридиана. Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 г

Системы высот

Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей. Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.

Высоты являются абсолютными, если их отсчитывают от основной уровенной поверхности, то есть от поверхности геоида. На рис. 2.5 отрезки отвесных линий Аа и Вв  абсолютные высоты точек А и В.

Высоты называют условными, если за начало счета высот выбрана какая-либо другая уровенная поверхность. На рис. 2.5 отрезки отвесных линий Аа и Вв  условные высоты точек А и В.

В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности. Численное значение высоты принято называть отметкой. Например, если высота точки А равна H_А = 15,378 м, то говорят, что отметка точки равна 15,378 м.

Рис. 2.5. Абсолютные и условные высоты: ab– уровенная поверхность;ab–поверхность геоида;Ab– уровенная поверхность точкиA;

Разность высот двух точек называется превышением. Так, превышение точкиВнад точкойАравно

h_AB = H_В  H_A.

Зная высоту точки А, для определения высоты точкиВна местности измеряют превышениеh_AB. Высоту точкиВвычисляют по формуле

H_В = H_A + h_AB.

Измерение превышений и последующее вычисление высот точек называется нивелированием.

Абсолютную высоту точки следует отличать от ее геодезическойвысоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2).Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.