43 Каноническое уравнения прямой в пространстве

Пусть прямая проходит через точку M1 (x1, y1, z1) и параллельна вектору (m ,n, l). Составим уравнение этой прямой.

Возьмем произвольную точку M (x, y, z) на этой прямой и найдем зависимость между x, y, z. Построим вектор

Векторы иколлинеарны.

- каноническое уравнение прямой в пространстве.

44 Параметрические уравнения прямой

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

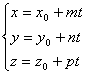
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:

Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

Отсюда получим: m : n : p = cosa : cosb : cosg.

Числа m, n, p называются угловыми коэффициентами прямой. Т.к.- ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

45 Уравнение прямой в пространстве, проходящее через две различные данные точки.

Аналитическая геометрия

Уравнение прямой, проходящей через две данные точки.

Пусть на плоскости даны М1(х1у1) и М2(х2у2). Составим каноническое уравнение прямой, проходящей через эти две точки в качестве направляющего вектора S возьмем M1M2

тройка.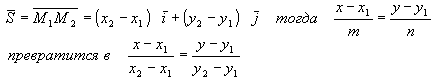

- это уравнение прямой, проходящей через две данные точки (х1 у1) и (х2, у2)

Перейдем теперь к уравнениям прямой и плоскости в пространстве.

Аналитическая геометрия в 3-мерном пространстве

Аналогично двумерному случаю любое уравнение первой степени относительно трех переменных x, y, z есть уравнение плоскости в пространстве Оxyz.. Общее уравнение плоскости АX + ВY + СZ + D = 0, где вектор N=(A,B,C) есть нормаль к плоскости. Каноническое уравнение плоскости, проходящей через точку М(х0,у0,z0) и имеющей нормаль N(А,В,С) А(х – х0) + В(у – у0) + С(z – z0)=0 – что представляет собой это уравнение?

Значения х –х0, у-у0 и z –z0 — это разности координат текущей точки и фиксированной точки. Следовательно, вектор а (х-х 0, у-у0, z-z0) -это вектор, лежащий в описываемой плоскости, а вектор N — вектор, перпендикулярный к плоскости, а значит, они перпендикулярны между собой.

Тогда их скалярное произведение должно равняться нулю.

В координатной форме (N,a)=0 выглядит так:

А·(х-х0)+В·(у-у0)+С·(z-z0)=0

В пространстве различают правые и левые тройки векторов. Тройка некомпланарных векторов а, b, с называется правой, если наблюдателю из их общего начала обход концов векторов a, b, с в указанном порядке кажется совершающимся по часовой стрелке. В противном случае a,b,c - левая .

46 Угол между прямыми в пространстве

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые: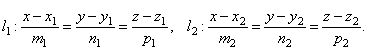

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и. Так как, то по формуле для косинуса угла между векторами получим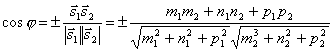

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и:

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен.

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Примеры:

Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:

Поскольку искомая прямая l параллельна l1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1.