
- •1.Методы координат на плоскости.
- •3.Уравнение прямой с угловым коэффициентом
- •4.Общее уравнение прямой
- •32. Скалярное произведение
- •33. Направляющие косинусы вектора
- •34. Векторное произведение
- •Свойства
- •38. Уравнением плоскости в отрезках.
- •39. Расстояние от точки до плоскости
- •40. Угол между плоскостями
- •41. Условие параллельности и перпендикулярности плоскостей
- •42 Общее уравнение прямой в пространстве
- •43 Каноническое уравнения прямой в пространстве
- •44 Параметрические уравнения прямой
- •45 Уравнение прямой в пространстве, проходящее через две различные данные точки.
- •46 Угол между прямыми в пространстве
- •47 Условия параллельности и перпендикулярности прямой и плоскости.
- •48 Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости.
- •49 Уравнение плоскости, проходящей через две данные точки перпендикулярной к данной плоскости.
- •50 Уравнение плоскости, проходящей через три данные точки не лежащие на одной прямой
32. Скалярное произведение
Скалярное
произведение векторов ![]() и
и![]() :
:![]() где
где
![]() -
угол между векторами
а и b;
если a=0,
либо b=0,
то
-
угол между векторами
а и b;
если a=0,
либо b=0,
то
![]()
Из
определения скалярного произведения
следует, что
![]() где,
например,
где,
например,
![]() есть
величина проекции вектора b
на направление вектора b.
Скалярный
квадрат вектора:
есть
величина проекции вектора b
на направление вектора b.
Скалярный
квадрат вектора:
![]()
Свойства скалярного произведения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скалярное произведение в координатах:
Если
![]() то
то
![]()
![]()
Угол
между векторами
![]()
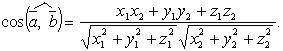
33. Направляющие косинусы вектора
Углы, образуемые вектором a с координатными осями Ox, Oy и Oz
![]()
![]()


![]()

![]()
![]()
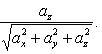
Косинусы, определяемые по этим формулам, называются направляющими косинусами вектора a
Для направляющих косинусов вектора имеет место формула
![]()
![]()
![]() т.
е. сумма квадратов косинусов углов,
образуемых вектором с тремя взаимно
перпендикулярными осями, равна единице.
т.
е. сумма квадратов косинусов углов,
образуемых вектором с тремя взаимно
перпендикулярными осями, равна единице.
Если
![]()
![]() т.
е. если а -
единичный вектор, обозначаемый обыкновенно
т.
е. если а -
единичный вектор, обозначаемый обыкновенно
![]() ,
то его проекции на координатные оси
вычисляются по формулам
,
то его проекции на координатные оси
вычисляются по формулам
![]()
![]()
![]()
![]()
![]() т.
е. проекции единичного вектора
т.
е. проекции единичного вектора
![]()
на оси прямоугольной системы координат Ox, Oy и Oz равны соответственно направляющим косинусам этого вектора. Имеет место формула
![]()
![]()
![]()
![]()
![]()
34. Векторное произведение
Векторное
произведение векторов a
и b
- вектор, обозначаемый ![]() или
или
![]() для
которого:
для
которого:
 (
( -
угол между векторами a
и b,
-
угол между векторами a
и b,
 )
)
Свойства векторного произведения:
![]()
![]()
![]()
![]()
![]()
![]()
Если
![]() ,
то
,
то
![]() равен
площади параллелограмма, построенного
на приведенных к общему началу векторах
a
и
b.
равен
площади параллелограмма, построенного
на приведенных к общему началу векторах
a
и
b.
Векторное произведение в координатах
Если
![]()
![]() то
то
![]()
Или


35.
Сме́шанное
произведе́ние
![]() векторов,
векторов,
![]() — скалярное
произведение вектора
а
на векторное
произведение векторов
b
и
с:
— скалярное
произведение вектора
а
на векторное
произведение векторов
b
и
с:
![]()
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами a, b, c
Свойства
1)
Смешанное произведение кососимметрично по
отношению ко всем своим аргументам:![]() т. е.
перестановка любых двух сомножителей
меняет знак произведения. Отсюда следует,
что
т. е.
перестановка любых двух сомножителей
меняет знак произведения. Отсюда следует,
что![]()
2)
Смешанное произведение
![]() в правой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов a,
b,
с
в правой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов a,
b,
с
3)
Смешанное
произведение
![]() в левой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов a,
b,c
взятому со знаком "минус":
в левой декартовой системе координат
(в ортонормированном базисе)
равно определителю матрицы,
составленной из векторов a,
b,c
взятому со знаком "минус":

частности,
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда, образованного векторами a, b,c; знак зависит от того, является ли эта тройка векторов правой или левой.
36. Уравнение плоскости, проходящей через точку с координатами (х0;у0;z0) перпендикулярно нормальному вектору плоскости с координатами (А,В,С)
A (x-x0) + B (y-y0) + C (z-z0)=0
37.
Неполные уравнения плоскости.
Если хотя бы одно из чисел А, В, С, D равно нулю, уравнениеAx + By + Cz + D = 0 называют неполным.
Рассмотрим возможные виды неполных уравнений:
1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.
2) А =
0 – n =
{0,B,C}![]() Ox,
следовательно, плоскость By + Cz + D =
0 параллельна оси Ох.
Ox,
следовательно, плоскость By + Cz + D =
0 параллельна оси Ох.
3) В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу.
4) С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz.
5) А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу).
6) А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz.
7) B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.
8) А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.
9) B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу.
10) C = D = 0 - плоскость Ax + By = 0 проходит через ось Oz.
11) A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху.
12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz.
13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.
