
- •1.Методы координат на плоскости.
- •3.Уравнение прямой с угловым коэффициентом
- •4.Общее уравнение прямой
- •32. Скалярное произведение
- •33. Направляющие косинусы вектора
- •34. Векторное произведение
- •Свойства
- •38. Уравнением плоскости в отрезках.
- •39. Расстояние от точки до плоскости
- •40. Угол между плоскостями
- •41. Условие параллельности и перпендикулярности плоскостей
- •42 Общее уравнение прямой в пространстве
- •43 Каноническое уравнения прямой в пространстве
- •44 Параметрические уравнения прямой
- •45 Уравнение прямой в пространстве, проходящее через две различные данные точки.
- •46 Угол между прямыми в пространстве
- •47 Условия параллельности и перпендикулярности прямой и плоскости.
- •48 Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости.
- •49 Уравнение плоскости, проходящей через две данные точки перпендикулярной к данной плоскости.
- •50 Уравнение плоскости, проходящей через три данные точки не лежащие на одной прямой
1.Методы координат на плоскости.
Основная идея метода координат на плоскости состоит в том, что геометрические свойства линии L выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнения F(x, y) = 0 этой линии. Например, геометрический вопрос о числе точек пересечения прямой и окружности сводится к аналитическому вопросу о числе решений алгебраической системы уравнений прямой и окружности.
В аналитической геометрии на плоскости систематически исследуются так называемые алгебраические линии 1 - го и 2 - го порядков; эти линии в декартовых прямоугольных координатах определяются соответственно алгебраическими уравнениями 1 - й и 2 - й степеней. Линии 1 - го порядка суть прямые и обратно, каждая прямая определяется алгебраическим уравнением 1 - й степени Ax + By + C = 0. Линии 2 - го порядка определяются уравнениями вида Ax² + Bxy + Cy² + Dx + Ey + F = 0. Основной метод исследования и классификации этих линий заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение линии имеет наиболее простой вид, и последующем исследовании этого простого уравнения.
В аналитической геометрии в пространстве декартовы прямоугольные координаты x, y, z (абсцисса, ордината и аппликата) точки М вводятся в полной аналогии с плоским случаем. Каждой поверхности S в пространстве можно сопоставить ее уравнение F(x, y, z) = 0относительно системы координат Oxyz. При этом геометрические свойства поверхности S выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнения этой поверхности. Линию L в пространстве задают как линию пересечения двух поверхностей S1 и S2. Если F1(x, y, z) = 0 и F2(x, y, z) = 0 - уравнения S1 и S2, то пара этих уравнений, рассматриваемая совместно, представляет собой уравнение линии L. Например, прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. В аналитической геометрии в пространстве систематически исследуются так называемые алгебраические поверхности 1 - го и 2 - г порядков. Выясняется, что алгебраическими поверхностями 1 - го порядка являются лишь плоскости. Поверхности 2 - го порядка определяются уравнениями вида: Ax² + By² + Cz² + Dxy + Eyz + Fzx + Gx + Hy + Mz + N = 0.
Основной метод исследования и классификации этих поверхностей заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение поверхности имеет наиболее простой вид, и последующем исследовании этого простого уравнения.
3.Уравнение прямой с угловым коэффициентом
В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.
Уравнение вида
![]() (1)
(1)
называется общим уравнением прямой.
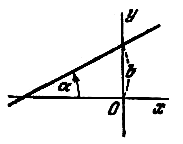
Угол ![]() ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:
,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:
![]()
Уравнение ![]() называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
Если прямая задана общим уравнением
![]() ,
,
то ее угловой коэффициент определяется по формуле
![]() .
.
Уравнение ![]() является
уравнением прямой, которая проходит
через точку
является
уравнением прямой, которая проходит
через точку ![]() (
(![]() ,
, ![]() )
и имеет угловой коэффициент k.
)
и имеет угловой коэффициент k.
Если
прямая проходит через точки ![]() (
(![]() ,
, ![]() ),
), ![]() (
(![]() ,
, ![]() ),
то ее угловой коэффициент определяется
по формуле
),
то ее угловой коэффициент определяется
по формуле
![]() .
.
Уравнение
![]()
является
уравнением прямой, проходящей через
две точки ![]() (
(![]() ,
,  )
и
)
и  (
(![]() ,
, ![]() ).
).
Если
известны угловые коэффициенты ![]() и
и ![]() двух
прямых, то один из углов
двух
прямых, то один из углов ![]() между
этими прямыми определяется по формуле
между
этими прямыми определяется по формуле
![]() .
.
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:![]() .
.
Признаком
перпендикулярности двух прямых является
соотношение
![]() ,
или
,
или ![]() .
.
Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
