3.Уравнение прямой с угловым коэффициентом

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

 (1)

называется общим уравнением прямой.

Угол , определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

Уравнение  называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением

,

то ее угловой коэффициент определяется по формуле

.

Уравнение  является уравнением прямой, которая проходит через точку  (, ) и имеет угловой коэффициент k.

Если прямая проходит через точки (, ), (, ), то ее угловой коэффициент определяется по формуле

.

Уравнение

является уравнением прямой, проходящей через две точки (, ) и (, ).

Если известны угловые коэффициенты  и  двух прямых, то один из углов  между этими прямыми определяется по формуле

.

Признаком параллельности двух прямых является равенство их угловых коэффициентов:.

Признаком перпендикулярности двух прямых является соотношение , или .

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

4.Общее уравнение прямой

Уравнение

Ах+Ву+С=0

(где А, В, Смогут иметь любые значения, лишь бы коэффициентыА, Вне были нулями оба сразу) представляетпрямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называютобщим уравнением прямой.

Если А=0, то есть уравнение не содержитх, то оно представляет прямую,параллельную оси ОХ.

Если В=0, то есть уравнение не содержиту, то оно представляет прямую,параллельную оси ОY.

Когла Вне равно нулю, то общее уравнение прямой можноразрешить относительно ординаты у, тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при Аотличным от нуля общее уравнение прямой можно разрешить относительнох.

Если С=0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат

5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом

Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

y - y₁ = k(x - x₁).     (1)

Это уравнение определяет пучок прямых, проходящих через точку A(x₁, y₁), которая называется центром пучка.

6. уравнение прямой, проходящей через две данные точки.

. Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

     (2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

     (3)

7. Уравнение прямой в отрезках

Если в общем уравнении прямой  , то разделив (1) на  , получаем уравнение прямой в отрезках

,

 

где  ,  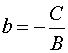. Прямая пересекает ось   в точке  , ось   в точке  .

8. Формула: Угол между прямыми на плоскости

Уголα между двумя прямыми, заданными уравнениями: y=k₁x+b₁ (первая прямая) и y=k₂x+b₂ (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1^й прямой ко 2^й против часовой стрелки):

tg(α)=(k2-k1)/(1+k1k2)

9. Взаимное расположение двух прямых на плоскости.

  Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

    и 

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1) если , то прямые  и  совпадают;

2) если , то прямые   и 

    параллельные;

3) если , то прямые пересекаются.

   Доказательство. Условие  равносильно коллинеарности нормальных векторов данных прямых:

. Поэтому, если , то  и прямыепересекаются.

   Если же , то , ,  иуравнение прямой  принимает вид:

 или , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

   Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.

Теорема доказана.