Algebra_i_geometriya / ІІІ модуль / NE_3.3 / приклади розв. задач до НЕ 3

Приклади розв’язування задач

Поліноміальні матриці

1. Звести матрицю до канонічного вигляду та знайти її інваріантні множники та елементарні дільники.

Розв’язання.

НСД мінорів 1-го порядку матриці

Мінори 2-го порядку:

Всі решта мінори 2-го порядку рівні нулю.

Мінори 3-го порядку:

Тому

Інваріантними множниками -матриці будуть многочлени

‑ вони стоять на головній діагоналі в канонічному вигляді матриці .

Отже, 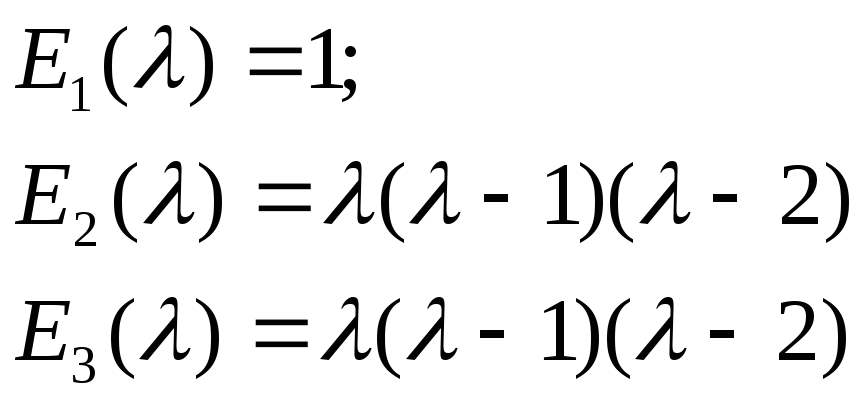‑ інваріантні множники

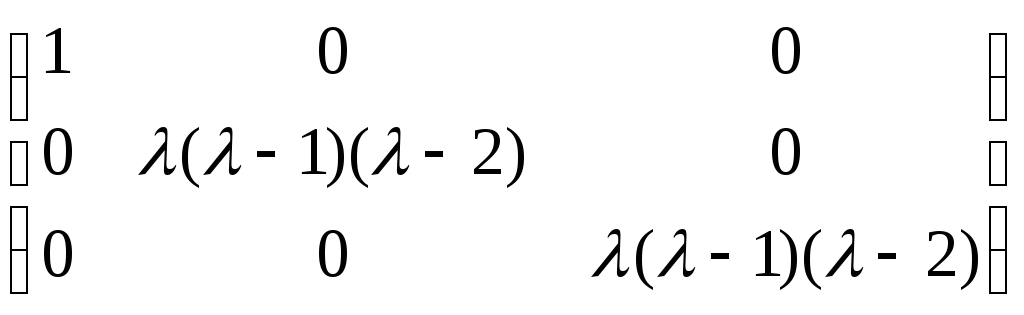~ ‑ канонічний вигляд

елементарними дільниками матриці є многочлени зі старшими коефіцієнтами = 1, які збігаються з найвищими степенями незвідних множників, які входять в розклади інваріантних множників матриці не незвідні множники.

Отже, елементарні дільники матриці наступні:

2. З’ясувати, чи числова матриця

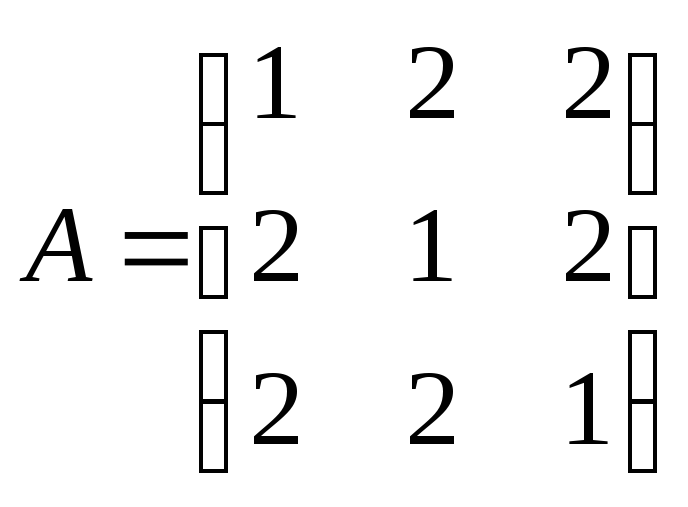
подібна до діагональної

Розв’язання.

Матриця В називається подібною до матриці А (А≈В), якщо ‑ невироджена матриця, така, що

Матриця а буде подібною до діагональної, якщо характеристичний многочлен не має кратних коренів.

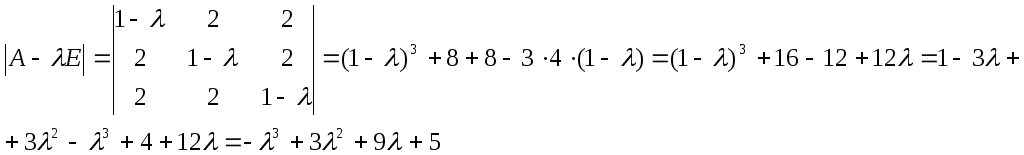
	1	-3	-9	-5
1	1	-3	-12	-17
-1	1	-4	-5	0

Отже, ‑ є два рівні характеристичні корені не подібна до діагональної.

3. Побудувати жорданову матрицю для матриці

Розв’язання.

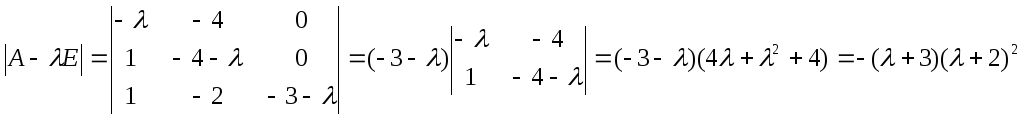
Характеристичному кореню відповідає клітка 1-го порядку, кореню відповідає клітка 2-го порядку. Отже,

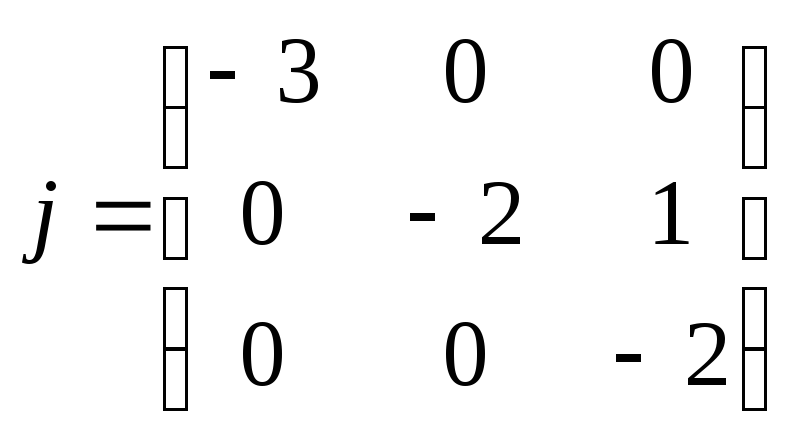~ ‑ жорданова форма матриці А.

2