§2.Аналіз перенормованого спектру полярона при скінченній температурі

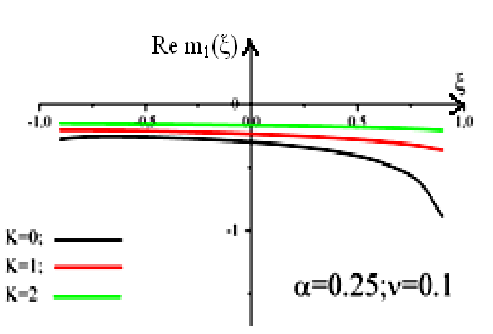
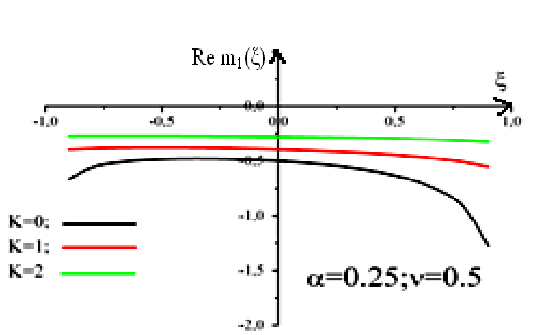
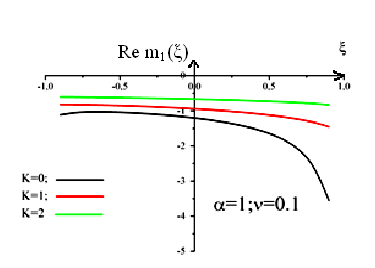
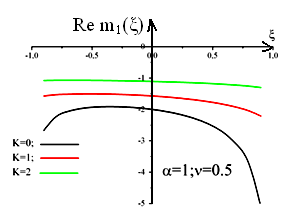
Для аналізу перенормованого спектру полярона спочатку вивчаємо властивості масового оператора як функції від безрозмірної енергії при різних значеннях квазіімпульса, при фіксованих значеннях константи зв’язку та скінченній температурі в однофононному наближенні. Для цього виконувався розрахунок дійсної та уявної частин однофононного масового оператора. Параметри вказані на рисунку 1.

а б

в г

Рис 1 .Залежності дійсної частини масового оператора від безрозмірної енергії при

фіксованих значення α, ν та k в однофононному наближенні.

На рисунку 1 наведена залежність дійсної частини масового оператора від безрозмірної енергії при фіксованих величинах α=0,25; α=1 та фіксованих значеннях температур ν=0,1 та ν=0,5 при різних значеннях квазіімпульса електрона. Як видно цього рисунка, зі збільшенням квазіімпульсу електрона спостерігається зміщення всього масового оператора як функції від ξ в область менших енергій. Чим більша константа зв’язку та температура, тим більше це зміщення.

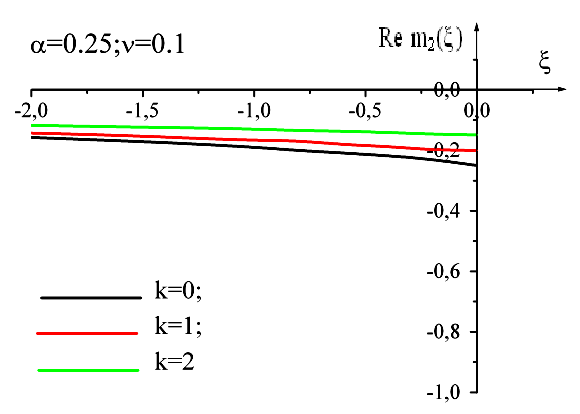
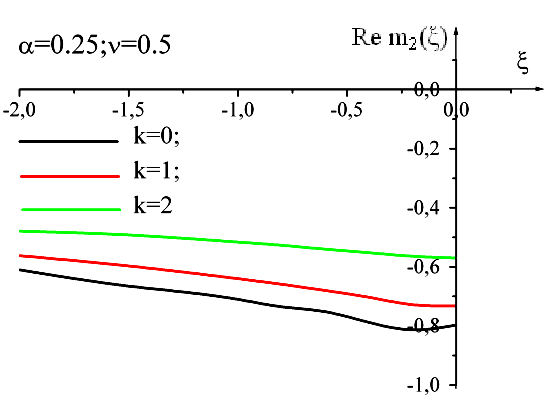
Вивчимо далі властивості масового оператора як функції від безрозмірної енергії при різних значеннях квазіімпульса, при фіксованих значеннях константи зв’язку та скінченній температурі в двофононному наближенні. Результат розрахунків приведено на рис2.

а б

Рис 2 Залежність дійсної частини масового оператора від безрозмірної енергії при фіксованих значення α, ν та k у двофононному наближенні.

З цього рисунку видно, що зі збільшенням квазіімпульсу та температури дійсна частина масового оператора зміщується в область менших енергій так як і в однофононному наближенні.

Для того,щоб отримати перенормований спектр в однофононному наближенні необхідно розв’язати безрозмірне дисперсійне рівняння:

розв’язки якого визначають () спектр полярона (залежність енергії від квазіімпульса). Результати дослідження приведені на рис 3

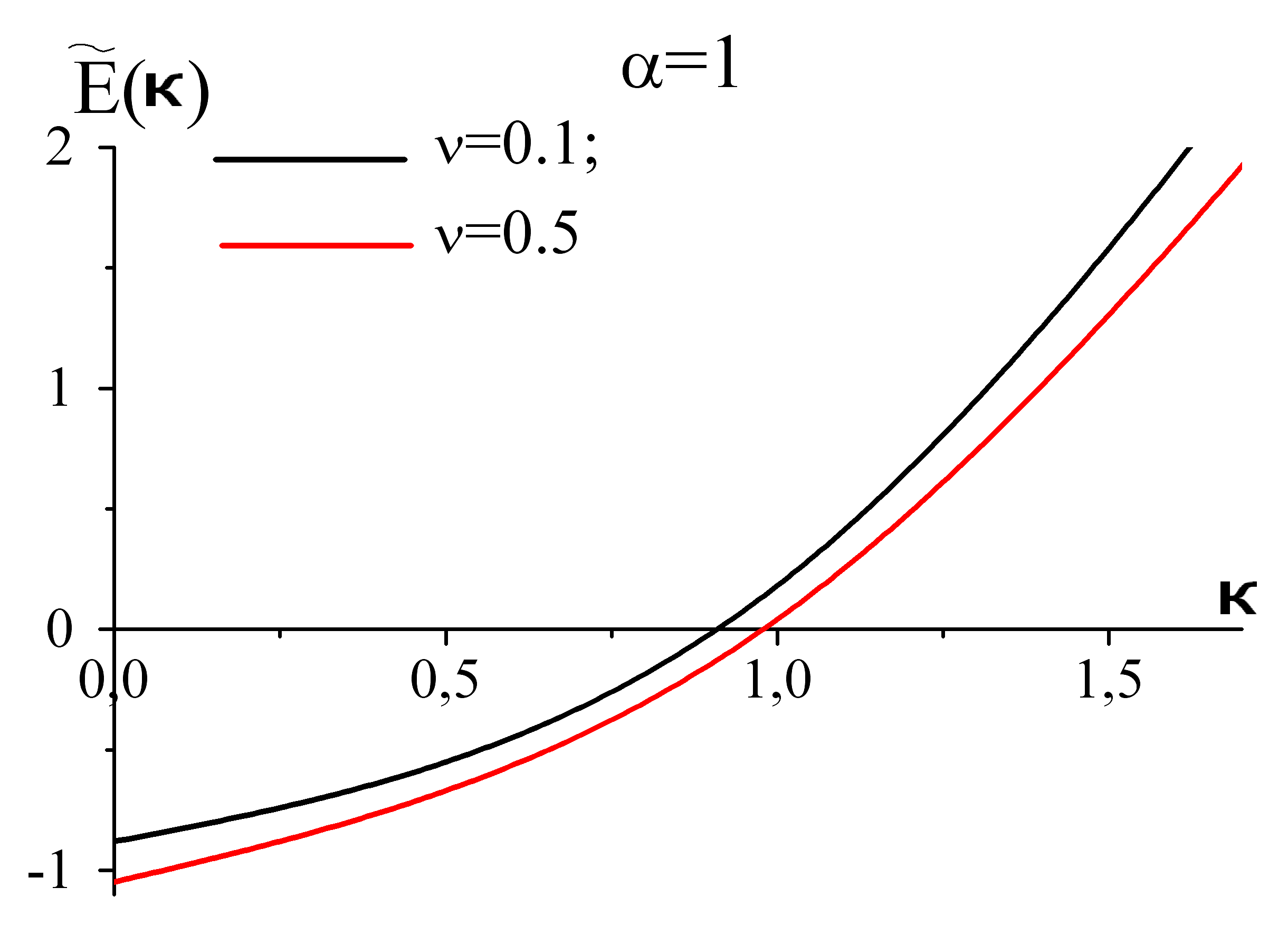
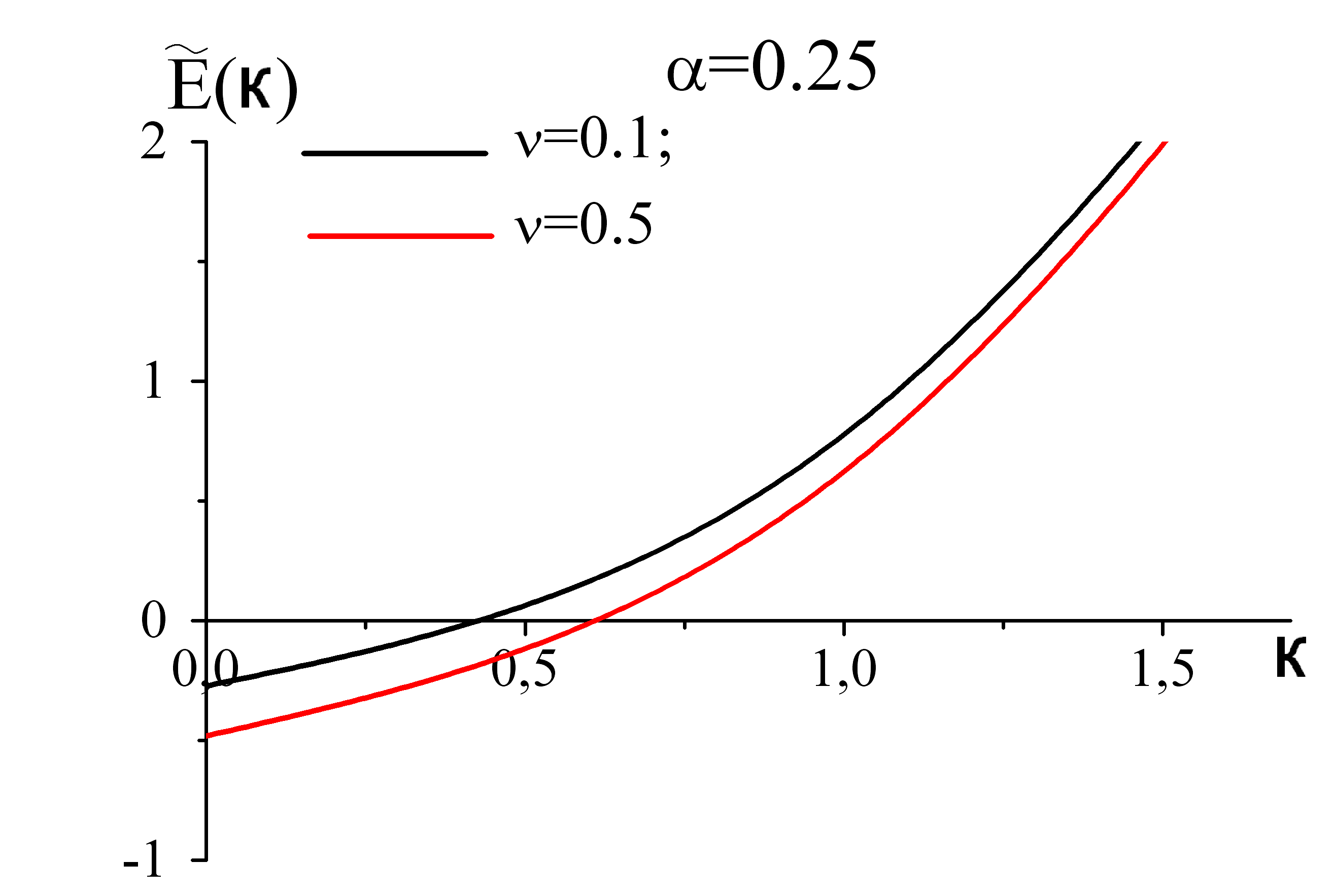
а б

рис 3 Залежність безрозмірної енергії від квазіімпульсу при фіксованих значеннях α та ν в однофононному наближенні

З рис3 видно, що при малих α зі збільшенням ν при малих К зміщення енергії більше ніж при великих. Це узгоджується з фізичними міркуваннями. Адже при великих значеннях квазіімпульса електрон “не встигає” взаємодіяти з фононами і вони не змінюють його енергії. З рис 3б видно при великих значеннях α зі збільшенням температури величина перенормованої енергії збільшується зі збільшенням квазіімпульсу, що протирічить фізичним міркуванням. З цього можна зробити висновок,що однофононного наближення не достатньо описує реальну ситуацію. Для отримання адекватної картини необхідно вивчити перенормований спектр полярона в двофононному наближенні.

Результат розрахунку перенормованого спектра в двофононному наближенні наведено на рис4.

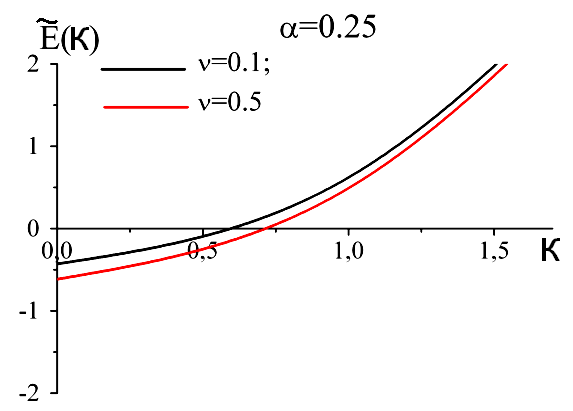
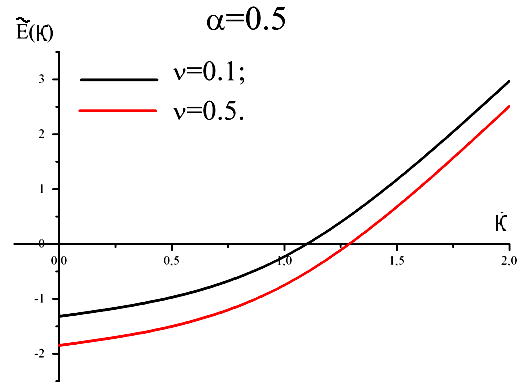
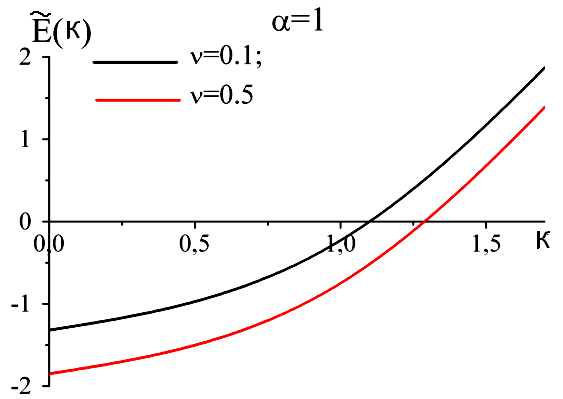
рис 4 Залежність безрозмірної енергії від квазіімпульсу при фіксованих значеннях α та ν в двофононному наближенні

З рис4, видно, залежність енергії від квазіімпульсу у двофононному наближенні є фізично коректною, так як збільшенням квазіімпульсу величина зміщення енергії зменшується. А зі збільшенням температури відбувається зсув всього закону дисперсії в область менших енергій у відповідності з фізичними міркуваннями.