§1.Аналітичний розрахунок масового оператора

Для того,щоб вивчити взаємодію з поляризаційними фононами спектр електрона при скінченній температурі системи будемо використовувати метод термодинамічних функцій Гріна. У рамках цього методу будемо описувати електрон-фононну систему гамільтоніаном Фреліха [9-12] у моделі діелектричного континууму та ефективних мас:

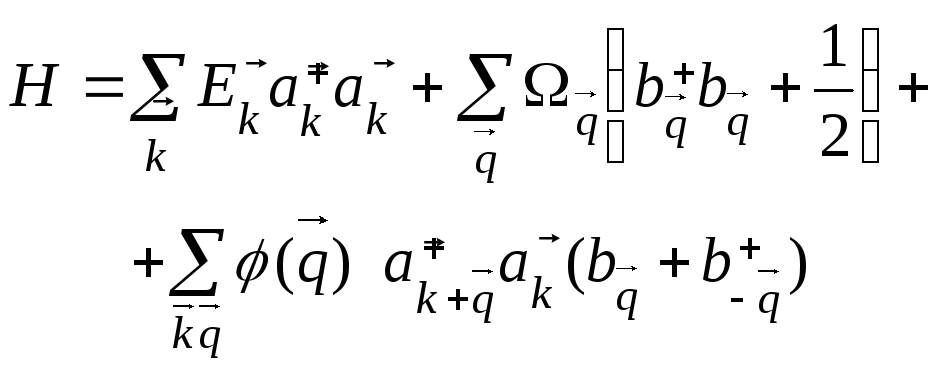(1.1)

де (1.2)

- відомий квадратичний закон дисперсії електрона

(1.3)

енергія бездисперсійних фононів

(1.4)

функція електрон-фононного зв’язку з константою Фреліха:

(1.5)

Як відомо з загальної теорії функції Гріна [9], перенормування спектра електрон-фононної системи визначається полюсами Фур’є-образу поляронної функції Гріна, яка рівнянням Дайсона (вважатимемо ħ=1)

(1.6)

пов’язана з повним масовим оператором (), який в свою чергу визначається згідно з діаграмною технікою Фейнмана-Пайнса[10] таким безмежним рядом

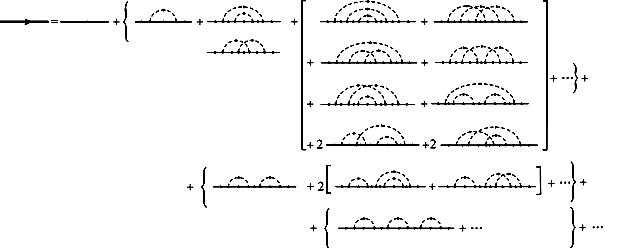
(1.7)

У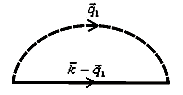випадку Т=0К при слабкому електрон-фононному зв’язку у повному масовому операторі достатньо обмежитися однофононним масовим оператором, тобто масовим оператором другого порядку за степенем функції зв’язку

(1.8)

Здійснивши перехід від суми до інтеграла

(1.9)

будемо виконувати аналітичний розрахунок безрозмірного масового оператора , використовуючи безрозмірні енергію ξ та квазіімпульси ():

; ;(1.10)

Виконавши точний аналітичний розрахунок масового оператора (1.8) отримується остаточний аналітичний вираз для

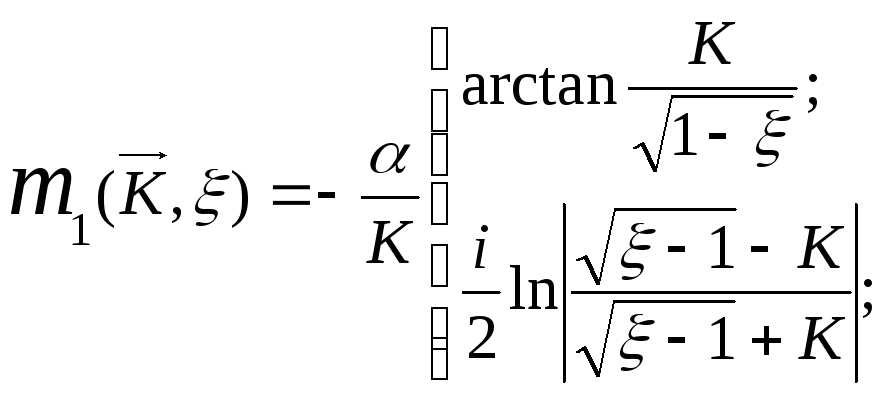
(1.11)

Для перенормування дна зони достатньо розглянути випадок =0.Тоді:

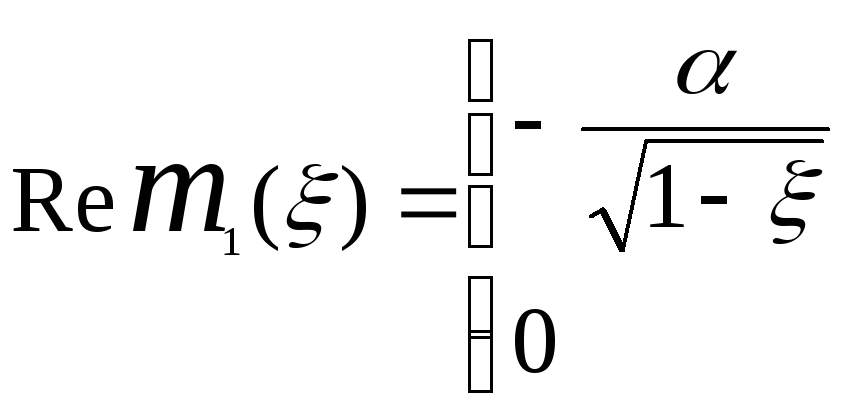
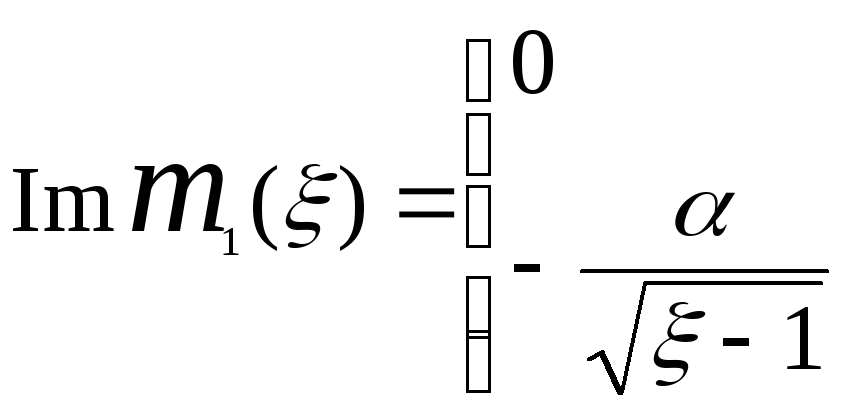
(1.12)

і перенормований поляронний спектр визначається розв’язками безрозмірного дисперсійного рівняння:

(1.13)

Тепер перейдемо до вивчення перенормованого поляронного спектру при довільній температурі системи. При Т≠0К необхідно враховувати температуру,від якої залежать середні числа заповнення. Вважається, що числа заповнення електронних станів нехтовно малі, тому враховується тільки середні значення фононних чисел заповнення:

(1.14)

Згідно з правилами діаграмної техніки Фейнмана-Пайнса масовий оператор другого порядку за степенем функції зв’язку у цьому випадку визначається так:

(1.15)

У безрозмірних змінних отримаємо масовий оператор у вигляді:

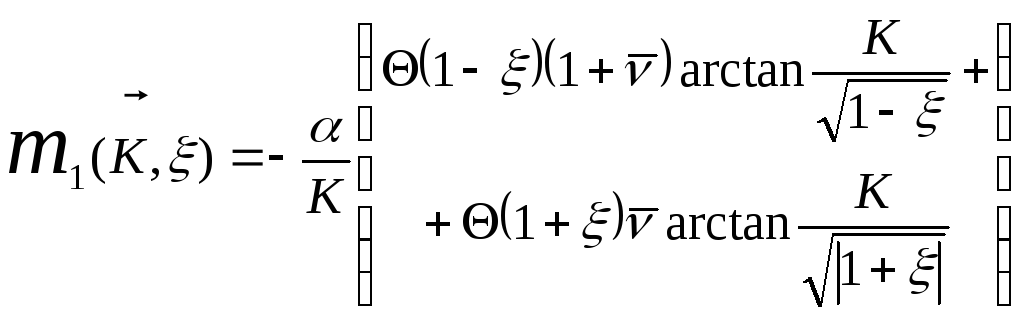(1.16)

який визначається в області безрозмірних енергій (-1;1). Масовий оператор в інших областях безрозмірних енергій отримується шляхом аналітичного продовження (1.16).

Розглянемо формулу (1.16). Вона описує залежність масового оператора від квазіімпульсу електрона та безрозмірної енергії. При К=0 отримаємо:

(1.17)

Аналіз і особливостей поляронного спектру на його основі буде виконано далі. Тут можна тільки зауважити,що оскільки в враховується взаємодія тільки з одним віртуальним фононом, то такий масовий оператор доцільно називати однофононним.

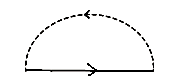
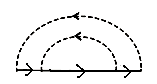
Розглянемо уточнений масовий оператор, який враховує не лише одно-, а й двофононні процеси у всіх порядках за константою зв’язку з урахуванням лише діаграм без перетинів фононних ліній.

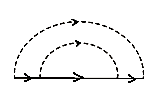
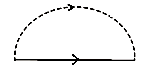
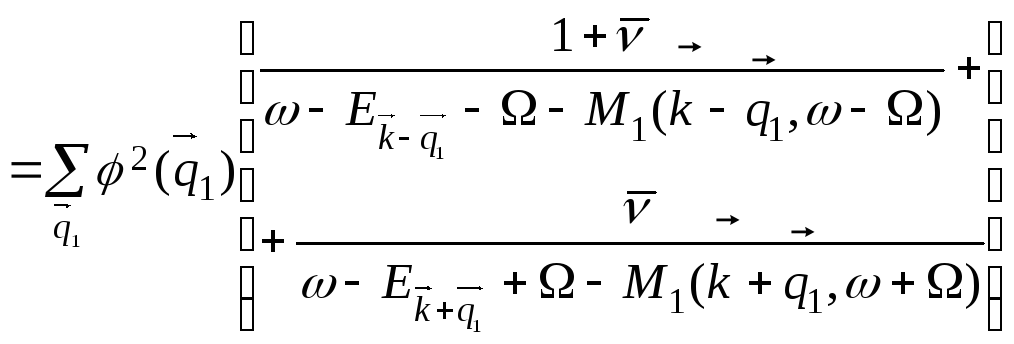
(1.18)

Підставивши значення та в (1.18) отримаємо:

(1.19)

Тут враховано,що оскільки квазіімпульс пробігає однаковий спектр додатніх і від’ємних значень, то .

Перейшовши у внутрішній сумі до інтеграла та нових змінних, отримаємо:

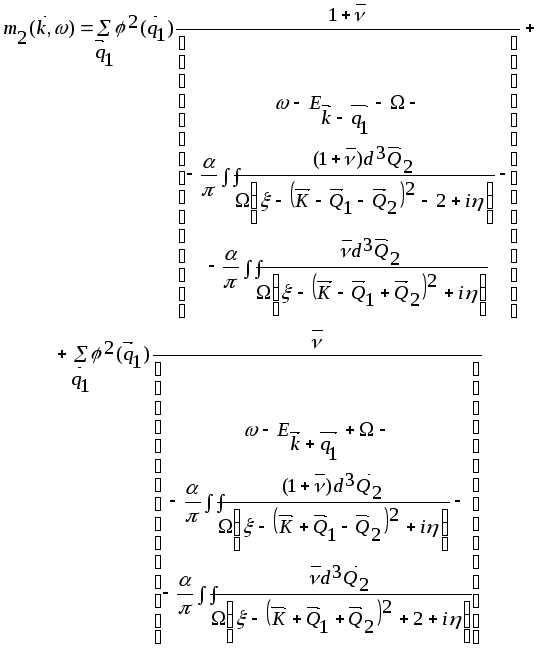
У безрозмірних позначеннях та після здійснення внутрішнього інтегрування отримаємо масовий оператор в області зміни ξ<0

(1.20a)

Для енергій 0<ξ<2 масовий оператор матиме вигляд:

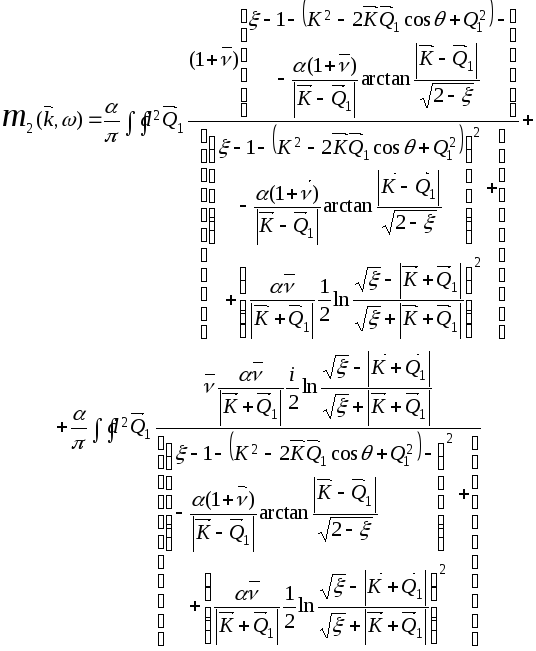
(1.20б)

Для енергій ξ>2 масовий оператора матиме вигляд:

(1.20в)

Подальші розрахунки інтегралів виконуються тільки числовими методами.