1 семестр / 2 лаб / Лабораторная работа2

Лабораторная работа №2

Расчет спектра одиночного прямоугольного импульса

Метод рядов Фурье допускает глубокое и плодотворное обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Для этого мысленно дополним одиночный импульс такими же импульсами, периодически следующими через некоторый интервал времени , и получим изученную ранее периодическую последовательность:

Представим одиночный импульс как сумму периодических импульсов с большим периодом .

, (14)

где - целые числа.

Для периодического колебания

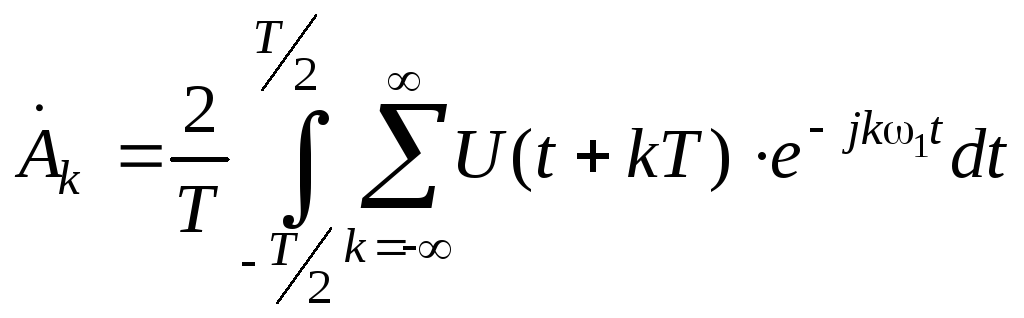. (15)

Для того, чтобы вернуться к одиночному импульсу, устремим к бесконечности период повторения: . При этом, очевидно:

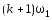1. Частота соседних гармоник и окажутся сколь угодно близкими (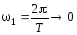), так что в формуле (15) дискретную переменную 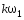можно заменить непрерывной переменной - текущей частотой, т.е. при увеличении периода колебаний 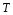составляющие спектра сгущаются по частоте и спектр одиночного импульса становится сплошным.

2. Амплитудные коэффициенты 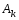станут неограниченно малыми из-за наличия величины 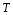в знаменателе формулы (15).

Имеем:

При

, (16)

где .

Обозначим

. (17)

Величиной называется спектральная характеристика (функция) одиночного импульса (прямое преобразование Фурье). Она зависит только от временного описания импульса и в общем виде является комплексной:

, (18)

где

; (19)

; (20)

,

где - модуль спектральной функции (амплитудно-частотная характеристика импульса);

- фазовый угол, фазо-частотная характеристика импульса.

Найдем для одиночного импульса по формуле (8), используя спектральную функцию:

.

Если , получим:

. (21)

Полученное выражение называется обратным преобразованием Фурье.

Интеграл Фурье определяет импульс в виде бесконечной суммы бесконечно малых гармонических составляющих, расположенных на всех частотах.

На этом основании говорят о непрерывном (сплошном) спектре, которым обладает одиночный импульс.

Полная энергия импульса (энергия, выделяемая на активном сопротивлении Ом) равна

(22)

Изменяя порядок интегрирования, получим

.

Внутренний интеграл есть спектральная функция импульса , взятая при аргументе -, т.е. представляет собой комплексно сопряженную с величину:

Следовательно

. (23)

- квадрат модуля (произведение двух сопряженных комплексных чисел равно квадрату модуля).

В этом случае условно говорят, что спектр импульса является двусторонним, т.е. размещается в полосе частот от до .

Приведенное соотношение (23), устанавливающее связь между энергией импульса (на сопротивлении 1 Ом) и модулем его спектральной функции известно под названием равенство Парсеваля.

Оно утверждает, что энергия, заключенная в импульсе , равна сумме энергий всех составляющих его спектра. Равенство Парсеваля характеризует важное свойство сигналов. Если некоторая избирательная система пропускает только часть спектра сигнала, ослабляя другие её составляющие, то это означает, что часть энергии сигнала теряется.

Так как квадрат модуля является четной функцией переменной интегрирования , то удвоив значение интеграла можно ввести интегрирование в пределах от 0 до :

. (24)

При этом говорят, что спектр импульса размещается в полосе частот от 0 до и называется односторонним.

Подынтегральная величина в (23) называется энергетическим спектром (спектральная плотность энергии) импульса

.

Она характеризует распределение энергии по частоте, и её значение на частоте равно энергии импульса, приходящейся на полосу частот, равной 1 Гц. Следовательно, энергия импульса есть результат интегрирования энергетического спектра сигнала по всему диапазону частот от до .Иначе говоря, энергия равна площади, заключённой между кривой, изображающей энергетический спектр сигнала и осью абсцисс.

Для оценки распределения энергии по спектру пользуются относительной интегральной функцией распределения энергии (энергетической характеристикой)

, (25)

где - энергия импульса в заданной полосе частот от 0 до , которая характеризует долю энергии импульса, сосредоточенную в интервале частот от 0 до .

Для одиночных импульсов различной формы выполняются следующие закономерности:

1. Спектры являются сплошными (непрерывными) и имеют один и тот же характер: основная энергия сосредоточена вблизи нулевой частоты; при увеличении частоты спектральная функция уменьшается.

2. Спектры бесконечно широкие, однако практически можно говорить о конечной ширине спектра, если отсечь высокие частоты, которые переносят незначительную часть энергии. Поэтому вводится понятие эффективной (активной) полосы частот спектра, в пределах которой сосредоточена основная доля энергии импульса (обычно 95 % полной энергии).

3. Основная часть энергии импульса расположена в полосе частот от 0 до .

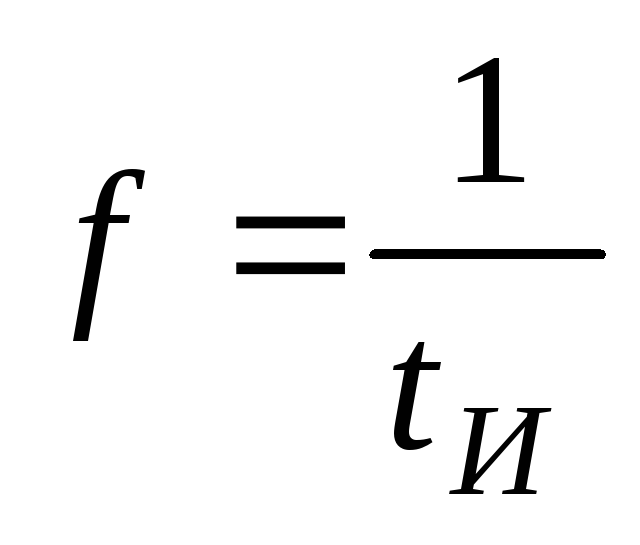4. Чем более плавный характер имеет форма импульса, тем быстрее спадает энергия с увеличением частоты, тем более « компактно » она сосредотачивается в диапазоне от нуля до частоты 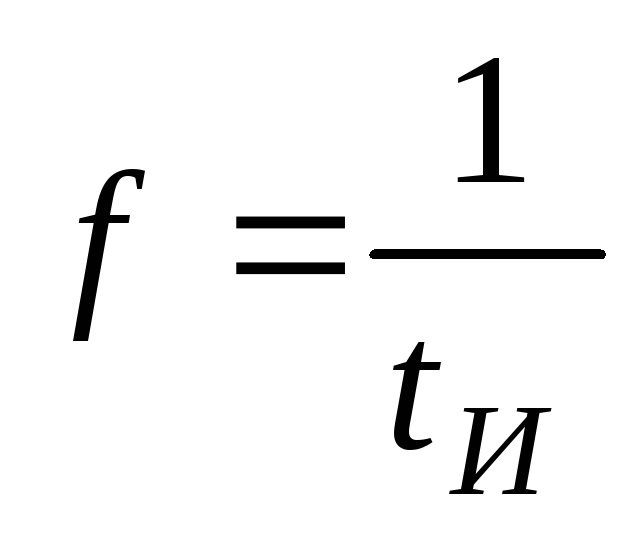, т.е. наибольшее влияние на форму вершины импульса оказывают низкочастотные составляющие спектральной функции, в то время как наиболее резко меняющиеся его части (фронт, срез) определяются высокочастотными составляющими спектра.

Всегда линейчатый спектр периодических импульсов вписывается в спектр одиночного импульса этой же формы (форма огибающей спектра периодических импульсов совпадает с формой спектра одиночного импульса).

Исходная функция (рисунок 6) имеет вид: .

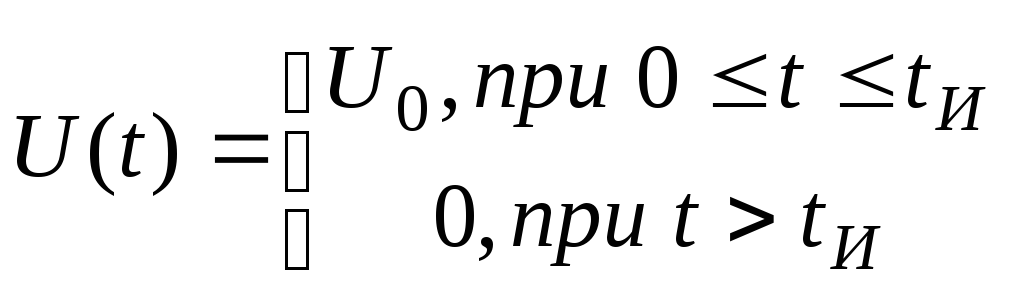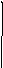
Рисунок 6

0

Спектральная характеристика определяется из соотношения

.

Преобразуем соотношение следующим образом

.

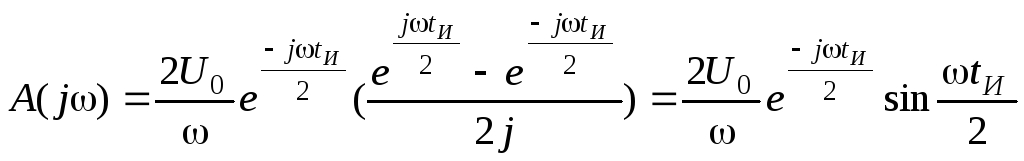Функция представляет собой модуль комплексного выражения (рисунок 7):

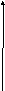
Рисунок 7

0

.

При

.

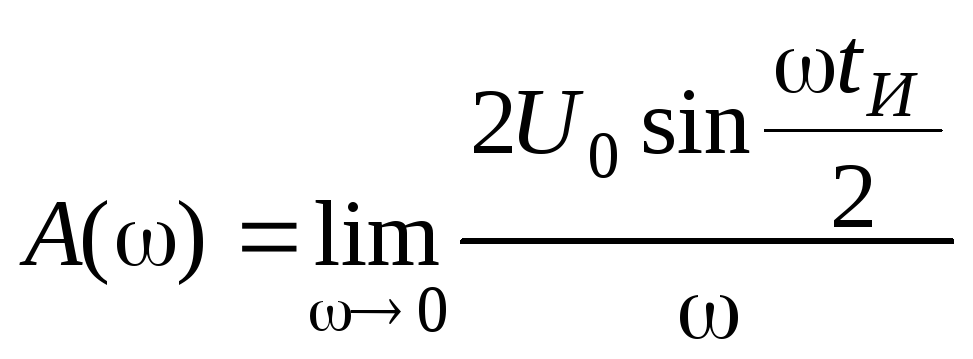Согласно правилу Лопиталя

.

Тогда

.

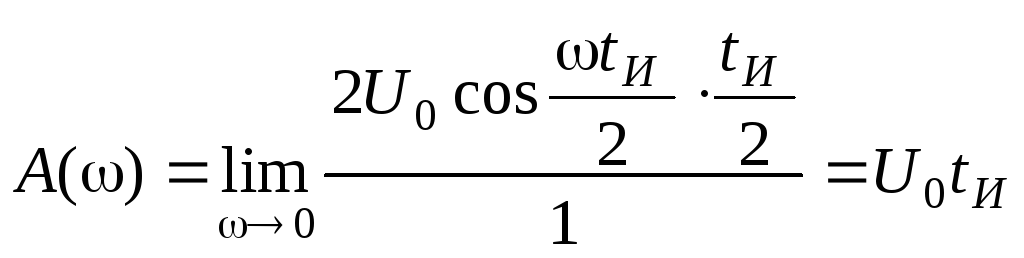Полная энергия одиночного прямоугольного импульса длительностью , выделяемая на активном сопротивлении Ом, определяется из соотношения(24): .

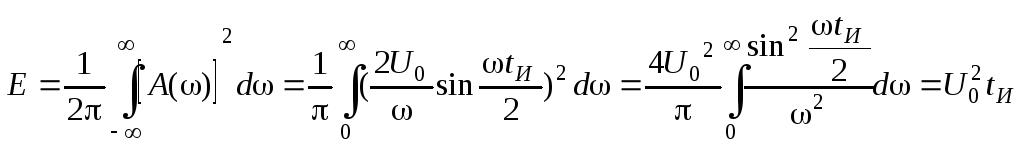С помощью равенства Парсеваля можно вычислить энергию одиночного импульса в заданной полосе частот от 0 до по формуле (23):

, (26)

где 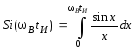- интегральный синус, значения которого приведены в приложении.

Энергетическая характеристика прямоугольного импульса для заданной полосы частот () примет вид:

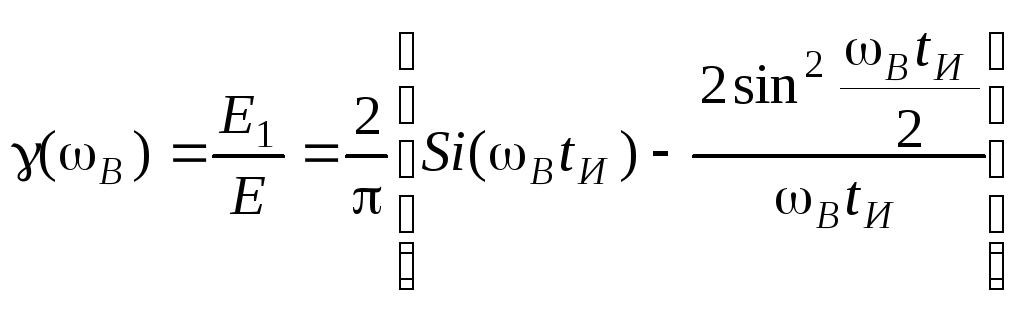. (27)

Пример расчета приведен на рисунке 8. По графику, например, можно найти эффективную полосу частот .

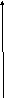
1

0.95

0

Рисунок 8

Обратное преобразование Фурье:

Задание:

Исходная функция прямоугольного импульса имеет вид: .

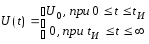1. Рассчитать и построить график функции (значения и берутся из задания к лаб. №1).

2. Рассчитать спектральную характеристику импульса и построить ее график. Построить график A(ω,t).

3. Рассчитать энергетическую характеристику импульса и построить.

4. Определить верхнюю частоту спектра сигнала при :

где - номер студента по журналу преподавателя.

5. Построить график импульса, используя обратное преобразование в полосе частот .

6. Выводы о проделанной работе.