Принцип суперпозиции

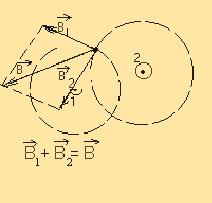
Для магнитного поля, как и для электрического поля, справедлив принцип суперпозиции: поле , порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей , порождаемых каждым зарядом (током) в отдельности:

т.е., чтобы найти силу, действующую на точку в пространстве, нужно сложить силы, действующие на неё, как показано на рисунке

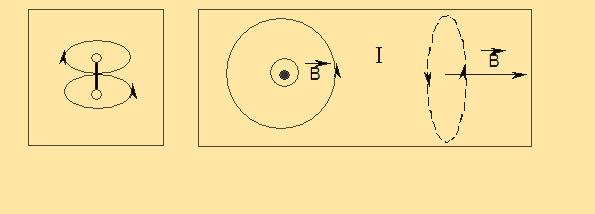
Магнитное поле кругового тока представляет собой некую восьмёрку с разделением колец в центре кольца, по которому течёт ток. Его схема показана на рисунке

28. Сила Лоренца. Движение заряженных частиц в магнитом поле.

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженнуючастицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью  заряд  лишь со сторонымагнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороныэлектрического  и магнитного  полей. Выражается в СИ как:

Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.  Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.  В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv²/r , следовательно   (1)  Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,    Подствавив (1), получим   (2)  т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц.  В случае, если скорость v заряженной частицы направлена под углом α к вектору В (рис. 170), то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью v_parall=vcosα ; 2) равномерного движения со скоростью v_perpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить v_perpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии    Подставив в данное выражение (2), найдем    Направление, в котором закручивается спираль, определяется знаком заряда частицы.  Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле. 

Рис.1

29. Эффект Холла и его применение.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 годув тонких пластинках золота.

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле  течёт электрический ток под действием напряжённости . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов  можно выразить через плотность тока:

где — концентрация носителей заряда. Тогда

Коэффициент  пропорциональности между  и  называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак , что объясняется в полуклассической и квантовой теориях твёрдого тела.