1.10.2. Способы отбора единиц из генеральной совокупности и необходимая численность выборки

В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения систематических и тенденциозных ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности.

Способы отбора единиц, применяемые в практике выборочного метода исследования, определяются правилами формирования выборочной совокупности, в зависимости от которых выборка может быть:

1) собственно-случайная – состоит в том, что выборочная совокупность получается в результате случайного отбора отдельных единиц из генеральной совокупности. Количество единиц выборки определяется исходя из принятой доли выборки. Примерами такой выборки может служить розыгрыш спортлото, жеребьёвка и т.д.;

2) механическая – состоит в том, что отбор единиц в выборку производится из генеральной совокупности, упорядоченной по признаку, не подлежащему изучению. Затем с определенным шагом выбирается необходимое число единиц, обратное величине заданной доли выборки. Так, при 5%-ной выборке механически отбирается каждая 20-я единица. По способу проведения механический отбор всегда бесповторный;

3) типическая – состоит в том, что генеральная совокупность вначале расчленяется на однородные типические группы, затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Отбор единиц может быть пропорциональным удельному весу каждой группы или непропорциональным. Типическая выборка применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников, состоящих из отдельных групп по квалификации. Типическая выборка даёт более точные результаты по сравнению с другими способами отбора единиц, что обеспечивается расчленением генеральной совокупности на качественно однородные группы и представительством в выборке (репрезентативностью) каждой типологической группы;

4) серийная (гнездовая) – состоит в том, что из генеральной совокупности отбираются не отдельные единицы, а целые их серии (гнёзда), причём внутри каждой серии обследуются все без исключения единицы. Серии могут быть как равновеликие, так и неравновеликие по численности;

5) комбинированная – заключается в том, что одновременно используются (комбинируются) несколько предыдущих способов отбора. Например, серийный отбор сочетается с собственно-случайным.

При организации выборочного наблюдения следует иметь ввиду, что размер ошибки выборки прежде всего зависит от численности выборочной совокупности . Из формулы для ошибки выборкивидно, что средняя ошибка выборки обратно пропорциональна, то есть при увеличении численности выборки, например, в 9 раз, ошибка выборки уменьшается только в 3 раза.

Определение необходимой численности выборки основывается на формулах для предельной ошибки выборки и. Необходимый объём выборки можно получить путём решения этих равенств относительно. Например, необходимая численность выборки при определении средней величины количественного признакавыразится формулой

в случае повторного отбора. Для бесповторного отбора имеет место формула

Необходимая численность выборки при определении доли альтернативного признака в генеральной совокупности рассчитывается по формуле

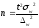
для повторного отбора и по формуле

для бесповторного отбора.