1.10. Выборочный метод в статистике

1.10.1. Понятие о выборочном исследовании

Статистическое исследование может осуществляться по данным несплошного наблюдения. Одним из наиболее распространённых в статистике методов, применяющих несплошное наблюдение, является выборочный метод. От других видов несплошного наблюдения (метода основного массива и монографического) выборочное наблюдение отличает принцип случайного отбора достаточно большого количества единиц исследуемой совокупности. Отобранная часть единиц должна представлять с уверенной степенью точности всю совокупность, что возможно, если отбор случайный и достаточный по количеству.

Под выборочным методом в статистике понимается метод статистического исследования, при котором обобщающие показатели изучаемой (генеральной) совокупности устанавливаются по некоторой её части на основе положений случайного отбора.

При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5–15%). Совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Часть единиц, отобранная из генеральной совокупности и подвергающаяся обследованию, называется выборочной совокупностью (выборкой).

Значение выборочного метода и его преимущество по сравнению с методами сплошного наблюдения состоят в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это важно в условиях рыночной экономики, требующих, чтобы эффект от применения результатов статистического исследования превышал затраты, понесенные на его проведение.

Содержание выборочного метода составляет система способов характеристики и правил отбора единиц изучаемой совокупности, которые будут рассмотрены далее.

Поскольку генеральная совокупность состоит из единиц с варьирующими признаками, то состав выборочной совокупности будет определённо в той или иной мере отличаться от состава генеральной совокупности, поэтому основной задачей при использовании выборочного метода является оценка возможной ошибки исследования. Объективно возникающее расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки, которая зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.

Возможные расхождения между характеристикой выборочной и генеральнойсовокупности измеряютсясредней ошибкой выборки .В математической статистике доказывается, что величина средней ошибки выборки определяется по формуле

где n – численность единиц выборки, – дисперсия генеральной совокупности. Генеральная дисперсия на практике, как правило, неизвестна, поэтому для определения средней ошибки используется дисперсия выборочной совокупности . Соотношение между дисперсиями в генеральной и выборочной совокупности имеет вид

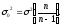
При достаточно большом значении n выполняется равенство поэтому для оценки средней ошибки выборки применяется формула

Эта оценка справедлива при повторном отборе единиц совокупности, который предполагает, что каждая зарегистрированная единица выборочной совокупности или их серия после обследования снова возвращаются в генеральную совокупность и в дальнейшем могут быть отобраны повторно.

При бесповторном отборе оценка средней ошибки выборки

где N – численность единиц генеральной совокупности. Бесповторное проведение отбора предполагает, что отобранная единица в генеральную совокупность не возвращается и в дальнейшем не может подвергаться повторному обследованию.

Дисперсия количественного признака в выборке определяется известной формулой

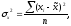
где ,– значения признака у отдельных единиц и среднее значение признака в выборочной совокупности, соответственно.

В выборочном методе могут изучаться два вида признаков – количественные (x) и альтернативные (w). Дисперсия альтернативного признака в выборочной совокупности для показателя доли признака определяется по формуле

.

Альтернативным признаком называют признак, который может принимать только два значения.

Пример 1. В корзине имеется совокупность чёрных и белых шаров.

Пример 2. Коллектив ткачих исследуется по признаку выработки, принимающему только два возможных значения: выработка ткачихи за смену менее 70 метров ткани и выработка 70 метров и более (невыполнение или выполнение нормы выработки).

Получаемое значение средней ошибки выборки позволяет определить один из возможных вариантов значений средней величины количественного признака в генеральной совокупности

и один из возможных вариантов значений, в пределах которых может находиться доля альтернативного признака во всей совокупности

.

В математической статистике доказывается, что пределы значений характеристик генеральной совокупности иp) отличаются от характеристик выборочной совокупности ина величину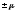лишь с вероятностью 0,683. Вероятность правильности суждений можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную враз. Например, при удвоенном значениивероятность правильного суждения достигает 0,954, а при утроенном – 0,997.

Предельную ошибку выборки находят по формуле

; ,

где –коэффициент доверия. Величина определяется по специальным таблицам в зависимости от заданного значениядоверительной вероятности F. Например, при величине требуемой доверительной вероятности коэффициент доверия