
- •Раздел 1. Теория статистики
- •1.1. Исходные понятия статистики
- •1.1.1. Предмет статистической науки
- •1.1.2. Методология и методы статистического исследования
- •1.1.3. Составные части статистики и их связь
- •Контрольные вопросы
- •1.2. Статистическое наблюдение
- •1.2.1. Требования к статистической информации
- •1.2.2. Организация статистического наблюдения
- •1.2.3. Виды статистического наблюдения
- •Контрольные вопросы
- •1.3. Статистическая сводка и группировка
- •1.3.1. Понятие о статистической сводке
- •1.3.2. Задачи и виды группировок
- •1.3.3. Выполнение группировки
- •1.3.4. Статистические таблицы
- •Контрольные вопросы
- •1.4. Статистические показатели
- •1.4.1. Сущность и виды показателей. Абсолютные и относительные величины
- •1.4.2. Средние величины, их сущность и их виды
- •9500 9600 9600 9600 9650 97009700 9900
- •4.3. Свойства и методы расчёта средних величин
- •Контрольные вопросы
- •1.5. Ряды распределения и графическое представление статистических данных
- •1.5.1. Ряды распределения
- •1.5.2 Графическое изображение вариационного ряда
- •1.5.3. Графическое представление статистических данных
- •Контрольные вопросы
- •1.6. Статистическое изучение вариации
- •1.6.1. Понятие вариации признака и показатели вариации
- •1.6.2. Дисперсия, её математические свойства и способы расчёта
- •1.6.3. Виды дисперсий, правило сложения дисперсий и его использование в анализе факторов
- •Контрольные вопросы
- •1.7. Статистическое изучение динамики явлений
- •1.7.1. Понятие о рядах динамики, их виды и правила построения
- •1.7.2. Аналитические показатели динамического ряда и способы их расчёта
- •1.7.3. Средние показатели в рядах динамики
- •Контрольные вопросы
- •Исследование развития явлений с помощью рядов динамики
- •1.8.1. Понятие тенденции ряда динамики и методы её выявления
- •I кв. – 9714 шт. III кв. – 11536 шт.
- •II кв. – 10115 шт. Iy кв. – 12242 шт.
- •1.8.2. Выравнивание уровней ряда динамики и типы развития социально-экономических явлений
- •1.8.3. Понятие об интерполяции и экстраполяции. Сезонные колебания
- •Контрольные вопросы
- •1.9. Индексный метод в статистических исследованиях
- •1.9.1. Назначение и виды индексов
- •1.9.2. Способы образования индексов и связь между ними
- •1.9.3. Выявление роли факторов динамики, структуры и взаиморасположения явлений индексным методом
- •Контрольные вопросы
- •1.10. Выборочный метод в статистике
- •1.10.1. Понятие о выборочном исследовании
- •1.10.2. Способы отбора единиц из генеральной совокупности и необходимая численность выборки
- •1.10.3. Способы распространения характеристик выборки на генеральную совокупность
- •Контрольные вопросы
- •1.11. Виды взаимосвязей и методы выявления корреляционных связей
- •1.11.1. Изучение взаимосвязей явлений – важнейшая задача статистики
- •1.11.2. Виды взаимосвязей
- •1.11.3. Статистические методы выявления корреляционной связи
- •Контрольные вопросы
- •1.12. Измерение взаимосвязей между явлениями
- •1.12.1. Описание взаимосвязей с помощью регрессионного анализа
- •1.12.2. Множественная регрессия
- •1.12.3. Измерение тесноты связи
- •Контрольные вопросы
1.9.3. Выявление роли факторов динамики, структуры и взаиморасположения явлений индексным методом
В рассмотренном ранее примере взаимосвязи общих индексов стоимостного объёма, цен и физического объёма имеет место соотношение

значение которого состоит в
том, что на его основе выделяется влияние
отдельных факторов (цены и физического
объёма) на изменение стоимостного объёма
товаров. Например, если общий уровень
цен на товары в отчётном периоде вырос
на 11,6% по сравнению с базисным периодом
( ,
а физический объём товаров вырос в
отчётном периоде на 7,5% (
,
а физический объём товаров вырос в
отчётном периоде на 7,5% ( ,
то индекс стоимостного объёма товаров
равен
,
то индекс стоимостного объёма товаров
равен
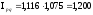 .
.
Т.е. стоимостной объём товаров вырос в отчётном периоде на 20,0% по сравнению с базисным периодом, что было обусловлено двумя факторами: а) ростом цен в среднем на 11,6%; б) увеличением физического объёма товаров на 7,5%.
При изучении динамики качественных показателей большое значение имеет определение изменения средней величины индексируемого показателя, которое обусловлено двумя факторами – изменением значений индексируемого показателя у отдельных групп единиц и изменением структуры совокупности. Например, из формулы средней цены

следует, что на её изменение
оказывает влияние как изменение цен на
отдельные товары
 ,
так и изменение числа отдельных товаров
,
так и изменение числа отдельных товаров в рассматриваемой совокупности.
в рассматриваемой совокупности.
Для анализа изменения
качественных показателей с помощью
средних величин (таких как средняя цена
 ,
средняя себестоимость единицы изделия
,
средняя себестоимость единицы изделия ,
средняя выработка работника
,
средняя выработка работника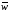 ,
средняя заработная плата работника
,
средняя заработная плата работника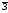 ,
средняя трудоёмкость изделия
,
средняя трудоёмкость изделия и др.) в статистической практике
применяются индексы средних величин,
которые зависят от соответствующих
индексов уровня и индексов структурных
сдвигов. В общем виде эта зависимость
следующая
и др.) в статистической практике
применяются индексы средних величин,
которые зависят от соответствующих
индексов уровня и индексов структурных
сдвигов. В общем виде эта зависимость
следующая

где

называется
индексом переменного
состава показателя
 (индексом среднего уровня), так как в
качестве весов-сомножителей в нём
выступают составы текущего
(индексом среднего уровня), так как в
качестве весов-сомножителей в нём
выступают составы текущего и базисного
и базисного периодов;
периодов;
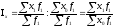
называется индексом
постоянного состава
показателя
 (общим индексом уровня или индексом
фиксированного состава), так как в
качестве весов-сомножителей в нём
выступает постоянный состав текущего
периода
(общим индексом уровня или индексом
фиксированного состава), так как в
качестве весов-сомножителей в нём
выступает постоянный состав текущего
периода ;
;

называется индексом
структурных сдвигов (индексом
структуры), так как в нём изменяются
лишь веса-сомножители состава совокупности
 и
и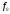 .
.
Рассмотрим пример. По известным
индексам уровня цен
 и структурных сдвигов
и структурных сдвигов необходимо определить, как изменилась
средняя цена товаров и за счёт влияния
каких факторов это изменение произошло.
необходимо определить, как изменилась
средняя цена товаров и за счёт влияния
каких факторов это изменение произошло.
Для ответа на этот вопрос надо рассматривать данные о структуре товара, т.е. рассматривать составляющие индекса средней цены

Таким образом, средняя цена товаров снизилась на 3,1%. Это произошло из-за изменения структуры товаров (в том числе за счёт увеличения доли дешевых товаров), хотя уровень цен на товары возрос в текущем периоде на 2,0%.
Для анализа соотношения явлений на различных территориях используются общие территориальные индексы (сравнения, взаиморасположения). Например, при изучении соотношения уровня цен на товары в различных городах (странах) исчисляют территориальные индексы цен

В этом случае общие (сводные)
индексы характеризуют соотношение цен
в городе А (стране А) по сравнению с
городом Б (страной Б в единой валюте).
Числитель индекса характеризует
фактический стоимостной объём данного
ассортимента товаров в городе А (стране
А). Знаменатель индекса
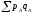 отражает условную величину стоимостного
объёма (в единой валюте) данного
ассортимента товаров в городе Б (стране
Б).
отражает условную величину стоимостного
объёма (в единой валюте) данного
ассортимента товаров в городе Б (стране
Б).
Соответствующий территориальный индекс физического объёма товаров определяют по формуле

Территориальный индекс стоимостного объёма товаров можно представит в виде

Последнее равенство выражает взаимосвязь между территориальными индексами стоимостного объёма, цен и физического объёма товаров.
