1.8.3. Понятие об интерполяции и экстраполяции. Сезонные колебания

Приближенный расчет уровней, лежащих внутри ряда динамики, но почему-либо неизвестных, называется интерполяцией. Такой расчет проводится на основе данных фактически сложившихся (реальных) уровней ряда на уже сложившемся определенном промежутке времени. Например, метод аналитического выравнивания уровней ряда динамики с той или иной степенью адекватности позволяет построить аппроксимацию (приближение) основной тенденции развития ряда динамики в виде аналитической функции y(t), дающей значения неизвестных уровней, лежащих внутри этого ряда. В этом случае интерполяция есть расчет неизвестных уровней с помощью адекватной математической функции фактически сложившегося ряда динамики, описывающего социально-экономическое явление.

Однако, основной целью анализа динамических рядов является не столько описание математическими методами и приёмами уже свершившейся динамики явлений, сколько получение на основе имеющихся данных научного анализа возможного развития явления в будущем.

Составление надёжных прогнозов динамики социальной и экономической деятельности является необходимым условием устойчивости регулирования социальных и рыночных отношений. Огромное значение при этом принадлежит методу экстраполяции.

Под экстраполяцией понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее. Другими словами, экстраполяция есть продление в будущее тенденции, наблюдающейся в прошлом.

Выводы по тенденции развития социально-экономических явлений, получаемые на основе экстраполяции, называют прогнозированием. Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, выступающего в качестве базы прогнозирования, сохраняется и в дальнейшем.

Возможность экстраполяции обеспечивается двумя обстоятельствами:

1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим уравнением.

Большое значение при экстраполяции имеет продолжительность базисного ряда динамики и сроки прогнозирования. Установление сроков прогнозирования зависит от задачи исследования, однако, следует иметь в виду, что чем короче сроки прогноза, тем надёжнее результаты экстраполяции.

Одной из основных задач анализа рядов динамики является выявление сезонных колебаний уровней социально-экономических явлений.

Под сезонными колебаниями понимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений. Проявляются они во всех сферах жизни общества: производстве, обращении, потреблении. Поэтому статистическое изучение сезонных колебаний имеет большое практическое значение.

В условиях периодической сменяемости сезонов жизнедеятельность людей сопровождается изменениями интенсивности динамики социально-экономических процессов. В большинстве отраслей экономики это проявляется в виде внутригодовых чередований подъёмов и спадов выпуска продукции, потребления сырья и энергии, производительности труда, себестоимости, прибыли и других показателей. Для некоторых сфер деятельности внутригодовая динамика характеризуется остановкой процессов в межсезонные периоды (сельское хозяйство, рыболовство, охота, навигация, туризм и т.д.). Значительным колебаниям во внутригодовой динамике подвержены денежное обращение и товарооборот.

Сезонные периодические колебания, которые имеют определенный ипостоянный период, равный годовому промежутку, встатистике также носят название сезонной волны, а динамический ряд в этомслучае называютсезонным рядом динамики. Измерение сезонных волн проводится различными методами, основанными на применении средней арифметической, относительных величин, механического (сглаживанием средних) и аналитического выравнивания. При изучении сезонных колебаний обычно прежде всего определяют общую тенденцию развития явления, исключают ее, а потом уже исчисляют показатели сезонности и производят их анализ.

Статистические ряды внутригодовой динамики составляются по материалам текущей отчётности, а для измерения сезонных колебаний обычно исчисляются индивидуальные индексы сезонности i_s. В общем виде они определяются отношением исходных (фактических) уровней ряда динамики к теоретическим (расчётным) уровням 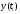, выступающим в качестве базы сравнения:

В результате того, что измерение сезонных колебаний проводится на базе соответствующих теоретических уровней тренда , в индивидуальных индексах сезонностивлияние основной тенденции развития устраняется (элиминируется). Глубина сезонных колебаний может определяется как размахом индивидуальных, так и средних индексов сезонности (в %).

Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности:

.

Для рядов внутригодовой динамики, в которых тренд отсутствует или незначителен, последняя формула приобретает вид:

,

где _i , – средний уровень показателя отдельного внутригодового периода и среднегодовое значение уровня, соответственно.