1.7.2. Аналитические показатели динамического ряда и способы их расчёта

Для количественной оценки динамики социально-экономических явлений применяются статистические показатели: абсолютные приросты, темпы роста и прироста, темпы наращивания и др.

Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется разностью двух уровней ряда динамики в единицах измерения исходной информации.

Базисный абсолютный прирост есть разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения

.

Цепной абсолютный прирост есть разность между сравниваемым уровнем 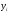и уровнем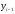, который ему предшествует:

.

Абсолютный прирост может иметь как положительный, так и отрицательный знак. Отрицательный знак показывает, насколько уровень показателя изучаемого периода ниже базисного.

Между базисными и цепными приростами имеется связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего рассматриваемого периода ряда динамики:

Распространённым аналитическим показателем динамики является темп роста.

Базисный темп роста исчисляется делением сравниваемого уровня на уровень принятый за постоянную базу сравнения:

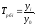
_{Цепной темп роста} исчисляется делением сравниваемого уровня 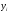на предыдущий уровень

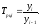
Если темп роста больше единицы (или 100 %), то это указывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице, показывает, что уровень изучаемого периода не изменился по сравнению с базисным. Темп роста меньше единицы указывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.

Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно последнему базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:

Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения.

Базисный темп прироста вычисляется делением сравниваемого базисного абсолютного прироста на уровень, принятый за постоянную базу сравнения

Цепной темп прироста – это отношение сравниваемого цепного приростак предыдущему уровню:

Темпы роста и темпы прироста могут быть рассчитаны как в коэффициентах, так и в процентах (коэффициенты, умноженные на 100%). Между показателями темпа прироста и темпа роста имеется взаимосвязь:

Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала.

Темпы наращивания вычисляются делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:

.

Иногда для оценки содержательной значимости прироста исчисляют абсолютное значение 1% прироста A_i как отношение прироста и темпа прироста за одни и те же периоды времени по формуле:

.