9500 9600 9600 9600 9650 97009700 9900

Порядковый номер медианы определяется по формуле

а) В случае чётного числа номер медианы имеет не целое значение (в нашем случае 4,5). Медиана будет равна средней арифметической из соседних значениии

б) В случае нечётного числа индивидуальных признаков (допустим, )

Следовательно, в этом случае

В рассмотренном примере нахождение таких средних, как мода и медиана, было целесообразно, поскольку исследователь не располагал объёмом продаж по каждому пункту и не мог поэтому с хорошей точностью провести расчёт средней арифметической цены за доллар. Также рассмотренный пример иллюстрирует положение о том, что выбор вида соответствующей средней всегда зависит от имеющихся в наличии данных.

4.3. Свойства и методы расчёта средних величин

Наиболее часто используемая в экономико-статистической практике средняя арифметическая величина обладает рядом математических свойств, которые иногда упрощают её расчёт. Эти свойства следующие:

1. Если варианты уменьшить или увеличить на некоторое постоянное число, то

средняя арифметическая величина соответственно уменьшится или увеличится на это число

2. Если варианты изменить в постоянное число раз то средняя тоже изменится во столько же раз

3. Если частоты разделить или умножить на некоторое постоянное число, то средняя не изменится

4. Произведение средней арифметической на сумму частот равно сумме произведений вариантов на частоты

5. Алгебраическая сумма отклонения вариантов от средней величины равна нулю

Все перечисленные свойства следуют из определения средней арифметической взвешенной (см. параграф 1.4.2).

Иногда расчёт средней арифметической величины удобно упростить, используя её математические свойства. Для этого нужно из всех вариант вычесть произвольную постоянную величину, полученную разность разделить на общий множитель, а затем исчисленную среднюю величину умножить на общий множитель и прибавить произвольную постоянную. В результате формула средней арифметической взвешенной получит следующий вид:

где .

Средняя величина из значений вариантназываетсямоментом первого порядка, а способ вычисления средней – способом моментов.

При выборе и расчёте вида средней величины необходимо учитывать наличие и характер исходных данных. Следует придерживаться следующего алгоритма.

1). Написать определяющее для расчёта среднего показателя соотношение, которое представляет собой суть связи между показателями задачи и определяет методологию расчёта обобщенного показателя. Например, если требуется определить среднюю месячную заработную плату работников, то таким соотношением является

где – средняя заработная плата;– фонд заработной платы;численность работников.

2). Изучить исходные данные и установить наличие показателей в определяющем соотношении. В предложенном примере такими показателями являются и. Если какой-либо показатель отсутствует, то его необходимо определить по исходным данным, пользуясь определяющим соотношением. Например, при наличии данных о фондах заработной платыи средней заработной платепо группам работников, недостающие показатели находятся в виде

3). Подставить недостающие показатели в определяющее соотношение и установить вид средней

т.е. в этом случае расчёт средней заработной платы можно выполнить по формуле средней гармонической взвешенной (см. параграф 1.4.2).

Соотношения для определения средних структурных величин, представленные в параграфе 1.4.2, предназначены для расчётов средних величин дискретных рядов. Методы расчёта средних по данным интервальных рядов имеют специфику, связанную с тем, что исследователь имеет дело не с дискретными значениями, а с интервалами группировочного признака. В этих случаях определения степенных средних сохраняются с учётом, что вместо значений вариант в них подставляются серединные значения признака в интервалах.

Для расчёта моды по данным интервального ряда используется следующая формула:

где – нижняя граница модального интервала;– размер модального интервала;– частота модального интервала;– частота интервала, предшествующего модальному;– частота интервала, следующего за модальным.

Для расчёта медианы в интервальном ряду используется следующая формула:

где – нижняя граница медианного интервала;– размер медианного интервала;– сумма накопленных частот до медианного интервала;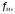– частота медианного интервала;– полу сумма частот ряда.