Расчет отвода

Действующие напоры в узлах главного направления создают в узлах отводов избыток напора над необходимым. Поэтому в случаях, когда запас напора достаточно большой (допускаемые потери напора в отводе по крайней мере в 2–2,5 раза превышают потери, соответствующие экономичным скоростям) и отсутствуют ограничения, накладываемые, например, противопожарными требованиями, в отводах можно применить трубы меньших диаметров по сравнению с принятыми для экономических скоростей.

1. Определяются наибольшие допустимые потери напора в отводе — расчетный напор отвода h_р — из зависимости (3.33), принимающей вид

(3.44)

где Н_н — напор в начале отвода (действующий напор главного направления в точке ответвления);

Н_к — необходимый напор в конечном узле отвода.

2. Находится наибольший допустимый гидравлический уклон на участках отвода по формуле:

(3.45)

где l — общая длина трубопроводов в отводе.

3. С помощью формулы (3.36) вычисляется наименьшее допустимое значение квадрата модуля расхода К² (наибольшее значение удельного сопротивления А) для каждого участка отвода. В данном расчете принимают =1, h/l = i.

4. По таблицам в зависимости от выбранного материала труб и величины К² (приложение 9) или [А] определяется ближайшее значение К² или А и соответствующий им стандартный диаметр d, но не больше величины d и К² принятых ранее для экономических скоростей.

5. Для участков отвода, на которых изменились диаметры трубопроводов и соответственно К² или А, определяются скорости движения воды с помощью формулы (3.28), коэффициенты  из таблицы (приложение 11) вычисляются потери напора по формуле (3.36).

6. Находятся действующие напоры в узлах отвода. Для этого решается система уравнений Бернулли (3.33), записанных для всех участков рассматриваемого отвода. Известными величинами являются потери напора на участках и напор в начале отвода Н_п. В процессе расчетов проверяется выполнение условия (3.39) в узлах отвода.

7. Если условие (3.39) не выполняется в каком-либо узле, то на участках перед ним диаметры трубопроводов увеличиваются до ближайшего значения, как указано в п. 4. После этого повторяются расчеты, предусмотренные в пунктах 5, 6.

8. По найденным значениям строятся соответствующие графики для отводов.

Пример расчета

Исходные данные и содержание задания.

Таблица 3.15 —Исходные данные

Узел	Отметка узла , м	Необходимый свободный напор Hсв, м	Расход Q, л/с	Участок	Длина участка l, м	Удельный расход q, (л/с)/м
0	64	–	–
1	62	12	2,6	0-1	165	–
2	63	14	3,2	1-2	390	–
3	63	12	2,9	1-3	360	0,01

Рисунок 3.12 — Расчетная схема водопроводной сети

Требуется:

1. Подобрать диаметры трубопроводов.

2. Определить действующие напоры H и расчетную высоту водопроводной башни H_Б.

3. Построить для водонапорной сети на бумаге с координатной сеткой график (линии) напоров: пьезометрического (действующего и необходимого) и геодезического (рисунок 3.12).

Расчет главного направления.

1. Определяем по формуле (3.42) расчетные расходы на участках сети. Для удобства расчетов сначала вычислим путевые, транзитные расходы:

а) путевой расход на участке 1–3:

б) транзитный расход:

– на участке 0–1

;

– на участке 1–2

;

– на участке 1–3

;

в) расчетные расходы:

– на участке 0–1

;

– на участке 1–2

;

– на участке 1–3

2. Выбираем в целях экономии металла асбестоцементные трубы, ГОСТ 539–73 (приложение 9). С помощью графика (рисунок 3.11) экономических скоростей определяем экономически выгодные диаметры трубопроводов на участках сети в зависимости от расчетного расхода. Принимаем ближайшее значение диаметра d для выбранного материала (приложение 9).

Определяем потери напора для каждого участка сети по формуле (3.36), предварительно определив по приложению 11 коэффициент . Результаты расчета приведены в таблице 3.16.

Таблица 3.16 —Результаты расчета

Участок	Q, л/с	d0, мм	dу, мм	υ, см/с	S, см2		l, м	h, м	K2, (л/с)2
0–1	12,3	141	150	80	156	1,03	165	0,9	31680
1–2	3,2	75	75	73	44	1,06	390	3,9	1204
1–3	4,7	100	100	60	78,5	1,08	360	1,8	5358

3. По формуле (3.37) находим необходимые напоры в каждом узле:

4. Определяем с помощью уравнения Бернулли (3.33) напор в начале сети, обеспечивающий работу потребителей, т. е. условие (3.39), обозначающее H = H, поочередно в каждом узле:

– для направления 01:

– для направления 02:

– для направления 03:

Наибольшим из полученных значений, т. е. искомый напор в начале сети, H₀ = H_02 = 81,8 м. Следовательно, диктующая точка — узел 2; главное направление: 0–1–2; отвод 1–3.

5. Определяем расчетную высоту водонапорной башни Н_Б из зависимости (3.42)

6. Находим действующие напоры в узлах главного направления. Для этого решаем систему уравнений Бернулли (3.33), записанных дли всех участков главного направления 0–1–2. В процессе расчетов проверяем выполнение условия (3.38) в диктующей точке и условия (3.39) в остальных узлах главного направления:

откуда

то есть больше

то есть

Расчет отводов

Выше было установлено, что в данном примере имеется отвод, состоящий из одного участка 1–3.

Определяем для него наибольшие допустимые потери напора (расчетный напор отвода), используя зависимость (3.43):

Данная величина почти в четыре раза превышает потери напора в трубопроводе, имеющем диаметр соответствующий экономичной скорости (100мм). Поэтому целесообразно проверить возможность применения трубопровода, имеющего меньший диаметр.

1. Для этого по формуле (3.44) находится наибольший допустимый средний уклон в отводе:

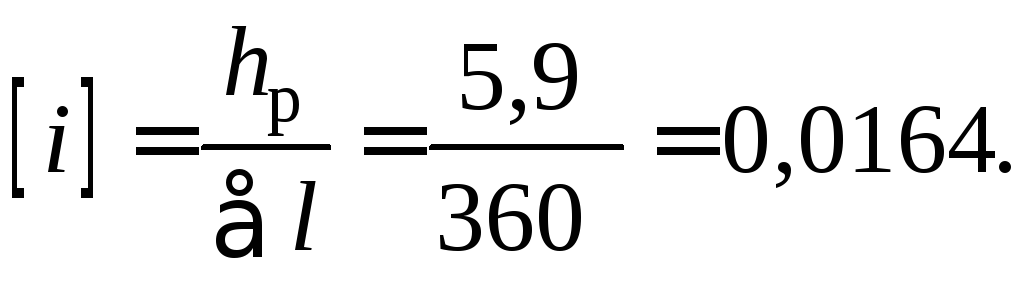
2. С помощью формулы (3.35) вычисляем наименьшее допустимое значение квадрата модуля расхода К² для участка отвода, приняв  = 1; (h/l) = i.

отвод 1–3

3. В зависимости от выбранного материала труб и величины К² находим, приложение 9, ближайшее значение квадрата модуля расхода К² и соответствующий ему диаметр d, но не больше величины К² и d для экономических скоростей.

В нашем случае отвод состоит из одного участка, поэтому принимаем d = 75 мм; К² = 1204 (л/с)² < 1482 (л/с)².

4. Для участка отвода 1–3, на котором изменился диаметр трубопровода, определяем скорость движения воды с помощью формулы (3.28), коэффициент  принимаем по приложению 11 и вычисляем потери напора по формуле (3.35):

5. Находим действующий напор в узле по уравнению Бернулли (3.33). Известными величинами являются потери напора на участке и напор в начале отвода H_н. В процессе расчетов проверяем выполнение условия (3.39) в узле отвода:

Из расчетов видно, что для d = 75 мм условие H H не выполняется. Следовательно, уменьшить диаметр трубы в отводе в данном случае нельзя и его следует оставить равным 100 мм.

Из приложения 9 видим, что ближайший меньший диаметр для асбестоцементных труб равен 75 мм. Следовательно, уменьшить диаметр труб в отводе в данном случае нельзя и его следует оставить равным 100 мм. Соответственно остаются без изменения и потери напора в отводе h_1-3 = 1,8 м.

Вычисляются действующие напоры в узлах отвода. В данном примере имеется только один участка отвода 1–3. В узле 1 напор определяется главным направлением, т. е. Н₁ = 80,9 м.

В узле 3 напор находится с помощью уравнения Бернулли, примененного для сечений 1 и 3, Н₁ = Н₃ + h_1-3. Отсюда

Н₃ = Н₁ – h_1-3 = 80,9 м – 1,8 м=79,1 м.

Н₃=75 м.

Результаты расчетов целесообразно оформить в виде таблицы 3.17.

Таблица 3.17 —Результаты расчетов

Направ-ление	Уча- сток	l	Расходы			d	h	Узел		Нсв	Н	Н	l
			Qт	Qп	Qр
		м	л/с	л/с	л/с	мм	м	№	м	м	м	м	м
гл.н.	0-1	165	12,3	–	12,3	141	0,2	0	64	–	–	81,8	0
	1-2	390	3,2	–	3,2	75	3,9	1	62	12	74	80,9	165
								2	63	14	77	77	555
отв.	1-3	325	2,9	3,6	4,7	100	1,8	1	62	12	74	80,9	165
								3	65	10	75	79,1	525
						Расчетная высота башни НБ, = 17,8м

По данным таблицы 3.17 строятся: напорная линия H = f₁(L), линия необходимых напоров H = f₂(L), и геодезическая линия Δ = f₃(L), (L — расстояние от водонапорной башни рассматриваемого узла сети (рисунок 3.13)).

Рисунок 3.13 — График напоров:

H — действующий; H — необходимый; Δ — геодезический; ----- — главное направление; - - - — отвод 1–3; Н_Б — высота башни; О — диктующая точка (узел 2)