Гидравлика / Практикум.

а) путевой расход на участке 1–3

Qп,1-3 q1-3 l1-3 0,01 л/с /м 360 м 3,6 л/с;

б) транзитные расходы:

на участке 0-1

Qт,0-1 Q1 Q2 Q3 Qп,1 3

2,6 л/с 3,2 л/с 2,9 л/с 3,6 л/с 12,3 л/с;

на участке 1-2

Qт,1-2 Q2 3,2 л/с;

на участке 1-3

Qт,1-3 Q3 2,9 л/с;

в) расчетные расходы:

на участке 0-1

Qр,0-1 Qт,0 1 12,3 л/с;

на участке 1-2

Qр,1-2 Qт,1 2 3,2 л/с;

на участке 1-3

Qр,1-3 Qт,1 3 0,5Qп,1 3 2,9 л/с 0,5 3,6 л/с 4,7 л/с.

2. Выбираем новые стальные водогазопроводные трубы (приложение 17). С помощью графика (рис. 6.25) экономических скоростей определяем экономически выгодные диаметры трубопроводов на участках сети в зависимости от расчетного расхода. Принимаем ближайшее значение внутреннего диаметра dв стандартных труб (приложение 17).

Определяем потери напора для каждого участка сети по формуле (6.16), предварительно определив по приложению 18 коэффициент . Результаты расчета представим в таблице 6.15.

302

Таблица 6.15

Результаты расчета

3. По формуле (6.17) находим необходимые напоры в каждом узле

Н 1 1 Нсв 1 62 м 12 м 74 м;Н 2 63 м 14 м 77 м;Н 3 63 м 12 м 75 м.

4.Определяем с помощью уравнения Бернулли (6.13) напор

вначале сети, обеспечивающий работу потребителей, т.е. условие (6.19), обозначающее H = [H], поочередно в каждом узле:

для направления 0 1

Н0 1 Н 1 h0 1 74 м 1,6 м 75,6 м;

для направления 0 2

Наибольшим из полученных значений, т.е. искомый напор в начале сети, H0 = H0→2 = 82,3 м. Следовательно, диктующая точка – узел 2; главное направление: 0–1–2; отвод 1–3.

5. Определяем расчетную высоту водонапорной башни Hб из зависимости (6.23)

Нб Н0 0 82,3 м 65 м 17,3 м.

303

6. Находим действующие напоры в узлах главного направления. Для этого решаем систему уравнений Бернулли (6.13), записанных дли всех участков главного направления 0–1–2. В процессе расчетов проверяем выполнение условия (6.19) в диктующей точке и условия (6.20) в остальных узлах главного направления

Н0 Н1 h0 1 ; Н1 Н2 h1 2 .

Откуда

Н1 Н0 h0 1 82,3 м 1,6 м 80,7 м > 74 м,

то есть условие (6.20) выполняется, так как

Н1 > Н 1 ,

Н 2 Н1 h1 2 80,7 м 3,7 м 77 м,

то есть условие (6.19) в диктующей точке выполняется, так как

Н 2 77 м.

Расчет отводов

Выше было установлено, что в данном примере имеется отвод, состоящий из одного участка 1–3.

Определяем для него наибольшие допустимые потери напора (расчетный напор отвода), используя зависимость (6.24)

hр Нн Н к Н1 Н 3 80,7 м 75 м 5,7 м.

Данная величина в два раза превышает потери напора в трубопроводе, имеющем диаметр соответствующий экономичной скорости (90 мм). Поэтому целесообразно проверить возможность применения трубопровода, имеющего меньший диаметр. Для этого:

1. По формуле (6.25) находится наибольший допустимый средний уклон в отводе

304

2. С помощью формулы (6.16) вычисляем наименьшее допустимое значение квадрата модуля расхода [K2] для участка отвода, приняв = 1, h/l = [i]. Для отвода 1-3

3.В зависимости от выбранного материала труб и величины [K2] находим по приложению 17, ближайшее значение квадрата модуля расхода K2 и соответствующий ему внутренний диаметр dв, но не больше величины K2 и dв для экономических скоростей.

В нашем случае отвод состоит из одного участка, поэтому принимаем dв = 79,5 мм; K2 = 1287 (л/с)2 < 2782 (л/с)2.

4.Для участка отвода 1–3, на котором изменился диаметр трубопровода, определяем скорость движения воды с помощью

уравнения неразрывности потока, коэффициент принимаем по приложению 18, и вычисляем потери напора по формуле (6.19)

5. Находим действующий напор в узле по уравнению Бернулли (6.13). Известными величинами являются потери напора на участке и напор в начале отвода Hн. В процессе расчетов проверяем выполнение условия (6.19) в узле отвода

Н3 Н1 h1-3 80,9 м 6,8 м 74,1 м 75 м.

Из расчетов видно, что для dв = 79,5 мм условие H ≥ [H] не выполняется. Следовательно, такой диаметр трубопровода применять нельзя. Из приложения 17 видим, что ближайший меньший диаметр для водогазопроводных стальных труб равен 79,5 мм. Таким образом, уменьшить диаметр труб в отводе в данном случае нельзя,

305

и его следует оставить равным 92,3 мм. Соответственно остаются без изменения и потери напора в отводе h1-3 = 3,3 м.

Вычисляются действующие напоры в узлах отвода. В данном примере имеется только один участка отвода 1–3. В узле 1 напор определяется главным направлением, то есть H1 = 80,9 м.

В узле 3 напор находится с помощью уравнения Бернулли, примененного для сечений 1 и 3, H1 = H3 + h1-3.

Отсюда

Н3 Н1 h1 3 80,9 м 3,3 м 77,6 м.Н 3 75 м.

Результаты расчетов целесообразно оформить в виде табли-

цы 6.16.

Таблица 6.16

Результаты расчетов

Расчетная высота башни Hб = 17,3 м

По данным таблицы 6.16 строятся: напорная линия H = f1(L), линия необходимых напоров [H] = f2(L) и геодезическая линияf3 L , где L – расстояние от водонапорной башни рассматриваемого узла сети (рис. 6.28).

306

6.4. Практическая работа «Расчет канала» Цель работы:

1.Овладеть навыками расчета каналов для транспортировки воды.

2.Построить поперечный профиль канала и сопоставить с гидравлически наивыгоднейшим сечением.

Общие сведения

Кан ал ом называется искусственное русло (водовод) с безнапорным движением воды, обычно устраиваемое в грунте.

По назначению каналы подразделяются на судоходные, оросительные, осушительные, обводнительные, водопроводные, канализационные, энергетические, комбинированные (комплексные) и др.

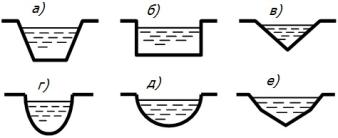
По форме поперечного сечения каналы подразделяют на следующие виды (рис. 6.29): а) трапецеидальные; б) прямоугольные; в) треугольные; г) параболические; д) круговые (сегментные); е) полигональные и др.

Рис. 6.29. Виды поперечного сечения каналов

Наибольшее распространение в практике гидротехнического

имелиоративного строительства получили трапецеидальные каналы (рис. 6.29, а). Такая форма позволяет обеспечить устойчивость откосов без специального крепления, а для сооружения канала требуется минимум капитальных затрат.

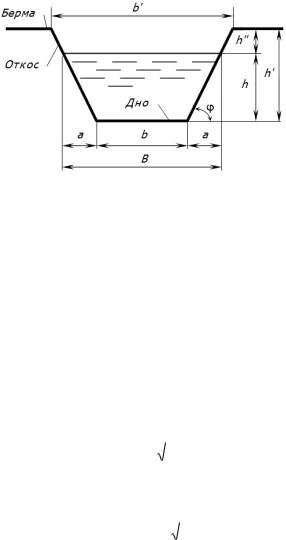
Основные геометрические характеристики трапецеидального канала следующие (рис. 6.30): b, b' и B - ширина по дну, по верху

ипо свободной поверхности воды соответственно; h - глубина заполнения водой; h' - общая глубина; h'' - превышение отметки бермы над отметкой уровня воды; a - заложение откоса; θ - угол наклона откоса; m - коэффициент заложения откоса.

308

Рис. 6.30. Поперечное сечение трапецеидального кана-

Коэффициент заложения откоса m = a/h = ct g θ выбирает-

ся в зависимости от прочности грунта, в котором проложен канал, а также от наличия и вида крепления откоса. Например, для необлицованного канала, проложенного в супесях или плотных песках, m = 1,5…2. Если откосы облицованы бетонными плитами,

то m = 1…1,5.

Основные морфометрические характеристики трапецеидального

При расчете каналов используют понятие нормальной глубины h0 - глубины заполнения канала, которая при заданных расходе Q и уклоне дна i устанавливается в условиях равномерного движения воды.

Равномерное движение воды в канале происходит только в цилиндрическом русле (т. е русле с неизменным поперечным се-

309

чением по длине) с прямым уклоном дна (i > 0) и при условии, что это русло достаточно длинное и не имеет каких-либо устройств, нарушающих равномерный режим (водосливов, перепадов, быстротоков, мостовых опор и т. п.).

Для расчетов каналов при равномерном режиме движения используют формулу Шези

или с учетом уравнения неразрывности (3.1)

где υ - средняя скорость; Q - расход воды;

С - коэффициент Шези (имеет размерность м0,5/с); i = i0 = I = sin ζ - продольный уклон дна канала;

i0 - продольный уклон свободной поверхности; I - гидравлический уклон;

ζ - угол между продольной линией дна канала и горизонтальной плоскостью;

W - модуль скорости;

K - модуль расхода.

Для определения коэффициента Шези С используются специальные таблицы, графики или эмпирические формулы различных авторов. Одна из них – формула Н.Н. Павловского

где n - коэффициент шероховатости, зависящий от состояния стенок и дна русла, числовые значения которого приводятся в справочной литературе (см. приложение 13).

В формуле (6.31) показатель степени y является функцией гидравлического радиуса R и коэффициента шероховатости n и определяется по полной формуле Н.Н. Павловского

Для приближенного вычисления y можно использовать формулы

310